Preregistration: Air Conditioner Test
Warning: None of the participants in the Great Air Conditioner Debate Of 2022 have endorsed my summaries of their positions in this post. Including me.
Background
In Everything I Need To Know About Takeoff Speeds I Learned From Air Conditioner Ratings On Amazon, I complained about the top-rated new air conditioner on Amazon. I claimed that it’s a straightforward example of a product with a major problem, but a major problem which most people will not notice, and which therefore never gets fixed. Specifically: although it does cool the room, the air conditioner also pulls hot air from outside into the house. People do notice the cool air blowing from the air conditioner, but don’t think to blame the air conditioner for hot air drawn into the house elsewhere. Simply adding a second hose would fix the problem at relatively low extra cost, and dramatically improve the effectiveness of the air conditioner. But companies don’t actually do that because (apparently) people mostly don’t notice the problem.
To my surprise, multiple commenters disagreed with my interpretation of the air conditioner example. They argue that in fact one-hose air conditioners work fine. Sure, single-hose air conditioners are less-than-ideally efficient compared to two-hose, but it’s not a very big difference in practice. CEER efficiency ratings account for the problems, and the efficiency difference is typically only about 20-30%. Also, The Wirecutter tested lots of portable air conditioners and found that there wasn’t much difference between one-hose and two-hose designs. (Credit to Paul for both those pieces of evidence.) Really, what this example illustrates is that simple models and clever arguments are not actually very reliable at predicting how things work in practice. One should instead put more trust in experiment and reported experiences, including all those 5-star ratings on Amazon.
I, on the other hand, think the “second hose doesn’t help much” claim is a load of baloney. I think it is far more probable that CEER ratings are bullshit and The Wirecutter messed up their test, than that a second hose makes only a small difference.
And so began The Great Air Conditioner Debate Of 2022.
… Why Do Air Conditioners Need Hoses?
Ideally, an air conditioner should work much like a fridge: it pumps heat from air inside to air outside. Inside and outside air do not touch or mix; only heat flows from one to the other.
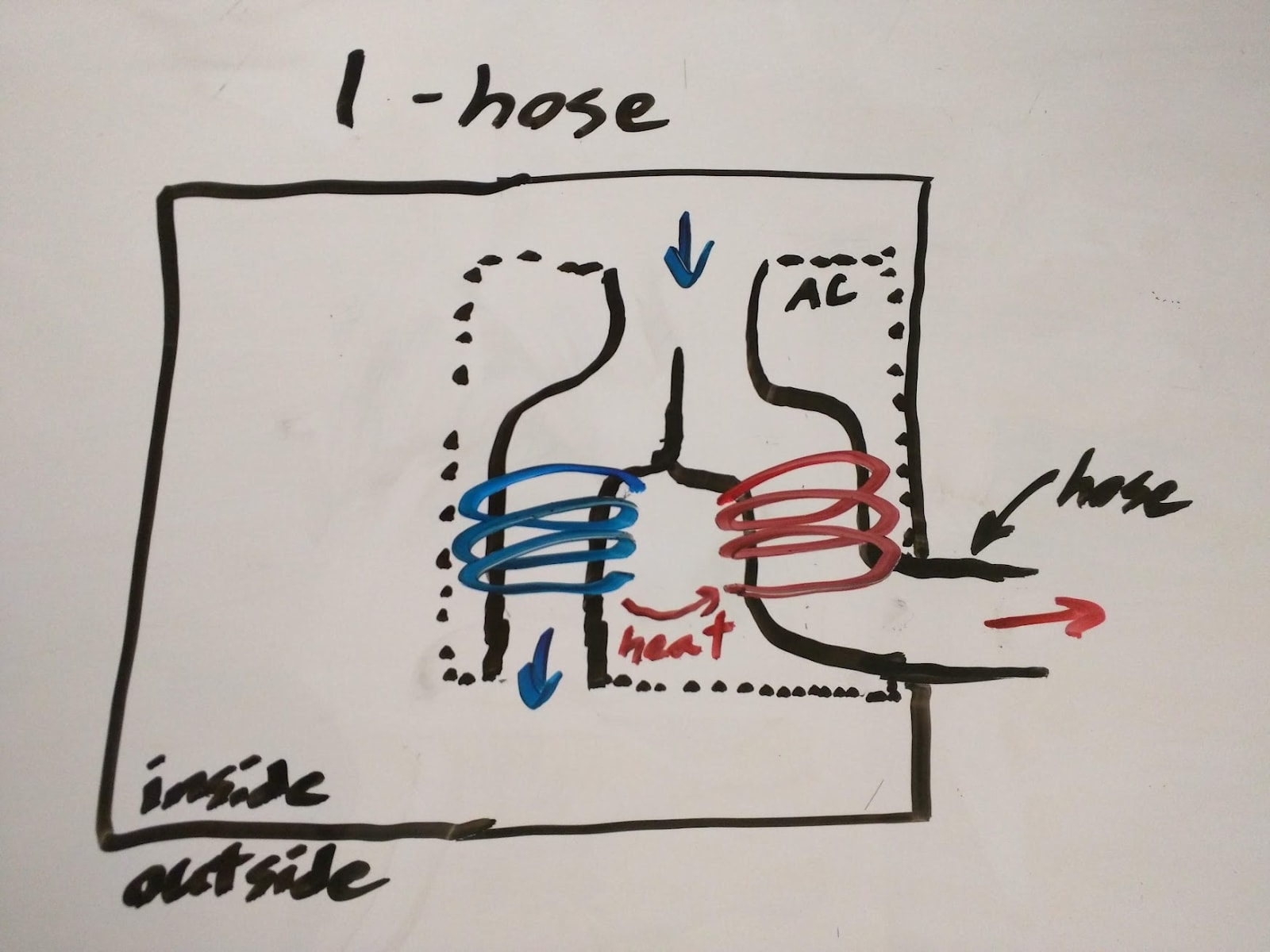
A portable air conditioner sits inside the house. So, in order to pump heat to the outside air (without letting it mix with inside air) it needs two hoses. One hose runs from a window to the air conditioner, and sucks in outside air. The other runs from the air conditioner back to the window, and blows the outside air back out. Inside air comes in and out through vents in the air conditioner, and the unit pumps heat from the inside air to the outside air, keeping the two separate throughout the process.
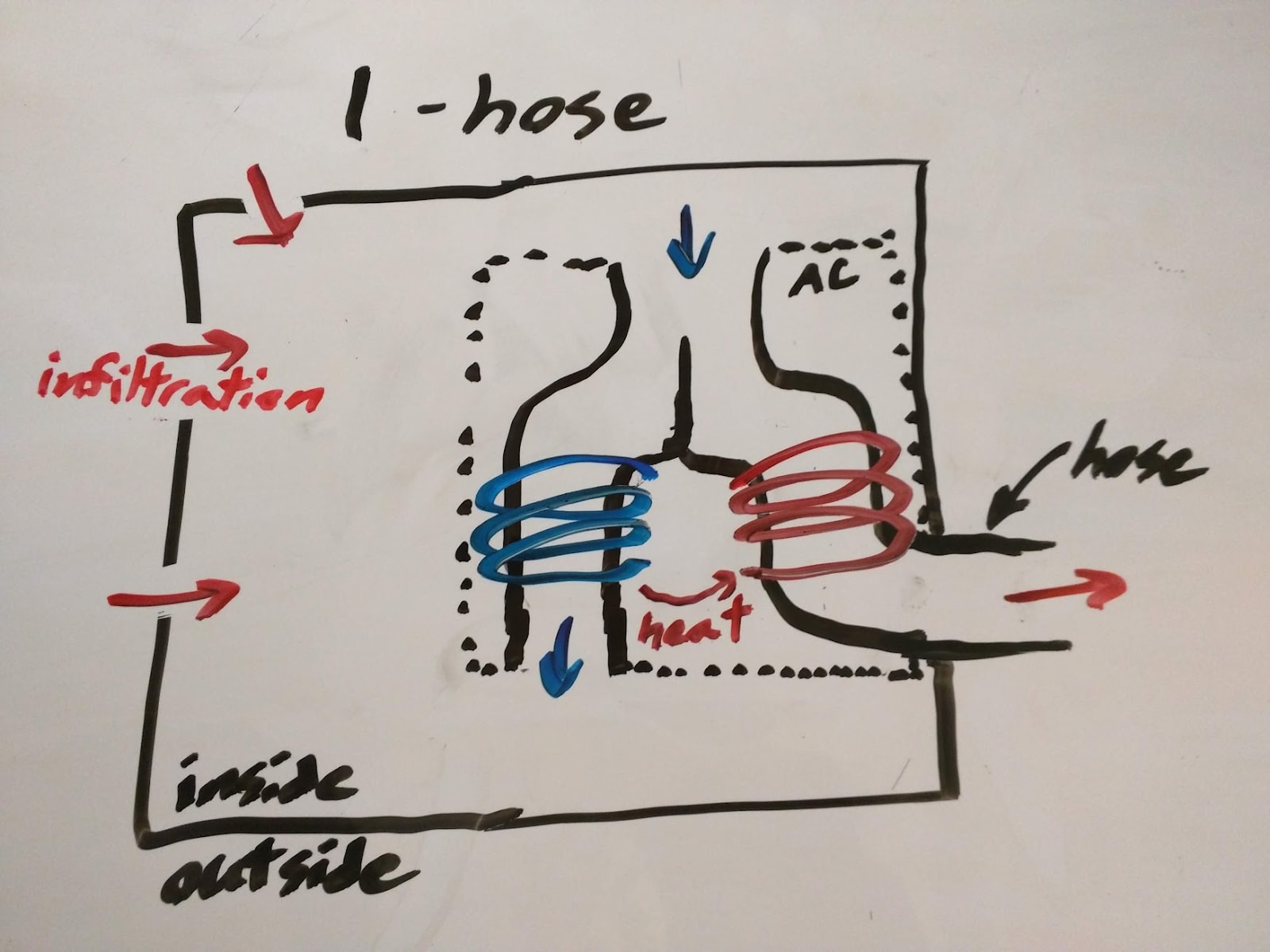
A single-hose air conditioner doesn’t do that. A single hose air conditioner sucks in indoor air, splits it into two streams, and pumps heat from one stream to the other. The hotter stream blows out the window (via the one hose); the cooler stream blows back into the room.
The problem with a single-hose design is that it blows air from inside to outside; it removes air from the room. That lowers the pressure in the room slightly, so new air is pulled back in via whatever openings the house has. That air comes from outside, so presumably it’s warm—and it’s replacing formerly-cool indoor air. (Technical term for this problem: “infiltration”.)
Oversimplified Summary Of The Debate
I’m not even going to try to do justice here, just give what I currently think are the key points, in roughly chronological order:
A couple people thought I was claiming that single-hose air conditioners do not cool a room at all. (I did not intend to claim that, though in hindsight I could see how the original post was unclear, so I added a clarification.) Paul, Shminux and jbash all correctly explained why single-hose air conditioners can cool a room: the exhaust is much hotter than outdoor air, so heat is removed on net even with some warm outdoor air coming back in.
Paul claimed that two-hose only improves efficiency by about 25-30%. He cited CEER ratings and The Wirecutter’s air conditioner tests (and provided some very helpful links). In particular, The Wirecutter did a direct comparison between the same air conditioner in one-hose and two-hose mode, and found little difference.
I called bullshit on The Wirecutter, and went looking for how their tests screwed up so badly. Paul showed that my first guess was completely wrong (after I was pretty sure it was right) and I lost some Bayes points (and actually came close to being convinced). But it eventually turned out that The Wirecutter was only measuring temperature within 6 feet of the unit.
Habryka looked into things, concluded that “The testing procedure of Wirecutter does not seem to address infiltration in any way”, but also that “Overall efficiency loss from going from dual to single is something like 20-30%”.
I also called bullshit on the “two-hose is only about 20-30% better” claim, and sketched out a test and bet. (More on that later in this post.) Ben also offered to run a test; I’m not sure whether he still intends to do so.
Since the 20-30% claim came largely from CEER ratings, I looked into the CEER test setup. Turns out that they use a weighted average of test conditions, with 80% of the weight on conditions where the difference between outdoor vs indoor temperature is only 3°F/1.6°C.
That last link includes some other important information too: one estimate that 20-30% lower CEER ratings imply one-hose air conditioners have roughly 0% efficiency under a 15°F/8.3°C temperature delta, as well as some quotes from discussion on the Department of Energy’s CEER rulemaking process suggesting that air conditioner manufacturers themselves thought single-hose units might not be viable in the marketplace at all if infiltration were fully included in ratings.
Paul and I each suggested a quantitative toy model during the discussion as well. Those models are in the appendix, for those interested.
Why Is This Interesting?
One thing to keep in mind throughout all of this: the actual claim of interest is that single-hose air conditioners are
stupidly inefficient in a way which I do not think consumers would plausibly choose over the relatively-low cost of a second hose if they recognized the problems.
Why are alignment researchers debating this claim?
There’s a general model/worldview that the world is filled with problems which are not fixed because most people do not notice them. (This is a particular form of “civilizational inadequacy”.) This includes problems which are bad enough that people would have a strong preference to fix the problem if they did notice it; we’re not just talking about small problems here. That worldview informs AI strategy: if we expect that ultimately-fatal problems with AI will not be fixed because most people do not notice them, then we’re generally more pessimistic about things working out all right “by default” and more reliant on doing things ourselves. Also, it means that we ourselves could easily miss the key problems, so we need to invest heavily in deep understanding, and in the kinds of models which tell us which questions to ask, and in techniques for noticing when our models are missing key pieces.
On the other hand, if we expect that major problems are usually noticed and fixed “by default”, and that AI will also work this way, that suggests very different strategies. We can rely more on marginal progress, making problems marginally more visible, helping existing institutions deal with problems marginally better, etc. We also don’t have to worry as much that we ourselves will miss the key problems for lack of understanding.
In general, alignment has terrible feedback loops: we can’t just build an AGI and test it. In this case, we can’t just have a team build an AGI and see whether any problems come up which the team missed. So if we want to test these two models/worldviews, then we need to get our bits from somewhere else. Fortunately, the real world is absolutely packed with bits of evidence; these worldviews make predictions in lots of different places, so there’s lots of opportunities to compare them.
In this case, the air conditioner example was cherry-picked, so even if my claims turn out to be correct it’s not very strong evidence for the civilizational inadequacy worldview in general. But if even my cherry-picked example is wrong, then that is a nontrivial chunk of evidence against the inadequacy worldview. I myself was almost convinced at one point during the debate, and started to think about how I’d have to adjust my priors on AI strategy in general (mostly it would have meant spending more effort researching questions which I had previously considered settled or irrelevant).
Also, we can update on the kinds of evidence and reasoning on display during the debate. For instance, many people took CEER ratings as strong evidence. If those indeed turn out to be bullshit, then it should produce a correspondingly strong update against trusting that kind of evidence in the future. Same with The Wirecutter’s tests.
Test Plan
I myself bought this single-hose portable air conditioner back in 2019 (for an apartment in Mountain View). My plan is to rig up a cardboard “second hose” for it, and try it out in my apartment both with and without the second hose next time we have a decently-hot day.
Particulars:
I plan to perform the test in a roughly 250 sq ft, roughly square bedroom. (Estimated dimensions; I haven’t measured it carefully.) It will not be in direct sun. The door will be closed.
I plan to open the outside door and window in the apartment’s main room and air it out beforehand, so any infiltration should be outdoor-temperature air. (So e.g. if the neighbor is running an AC, I shouldn’t suck in their cool air.)
I plan to wait for a day when it’s at least 80°F/26.7°C outside. AC will be set to its minimum temperature (60°F/15.6°C).
I am assuming that the AC runs continuously (as opposed to getting the room down to target temperature easily, at which point it will shut off until the temperature goes back up). If that’s not the case, I will consider the test invalid, and retry on a hotter day.
I plan to run the AC until the temperature distribution in the room equilibrates (i.e. my temperature measurements stop noticeably trending), then measure temperatures. I expect that will take under an hour, but I’m not sure.
If there are other particulars of the experiment which people think will be relevant, leave a comment and I’ll declare how I plan to control the variables in question.
Predictions
The main experimental endpoint I plan to test is temperature, not efficiency. Specifically, once the temperature equilibrates, I plan to check air temperature at nine points around the room (4 corners, midpoint of each wall, and center) at roughly head height, average them, and also check temperature outside around the same time. The main outcome of interest will be the difference in temperature between inside and outside (“equilibrium temperature delta”). Two reasons for testing equilibrium temperature delta rather than efficiency:
Equilibrium indoor temperature was the main thing I cared about when using this air conditioner; electricity is relatively cheap.
I don’t have the equipment on hand to easily measure power consumption.
Main prediction: equilibrium temperature delta in two-hose mode will be at least 50% greater than in one-hose mode. Example: suppose it’s 80°F/26.7°C outside. In one-hose mode, the average equilibrium temperature in the room is 75°F/23.9°C (temperature delta = 5°F/2.8°C). Then I expect the average equilibrium temperature in two-hose mode to be below 72.5°F/22.5°C (temperature delta > 7.5°F/4.2°C).
Confidence: originally I put 80% on this. After finding the problem with CEER ratings, I think I’m up to more like 90%. My median expectation is that equilibrium temperature delta in two-hose mode will be ~double the equilibrium temperature delta in one-hose mode.
Paul disagrees with this, and expects the two-hose temperature delta to be more like 20% greater than the one-hose delta (roughly proportional to the efficiency difference he expects). [EDIT: Paul clarified that he expects a 25-30% efficiency difference, which he expects to translate into a 33-43% difference in temperature delta. He also listed a few conditions under which that prediction would change. 33-43% is pretty close to my 50% cutoff, though my median expectation is much bigger, so we do still have a substantive disagreement to test.]
Prediction Market & Bets
There’s a Manifold prediction market for the experiment here. If you want everyone to see your probability on LessWrong, you can also use this prediction widget:
If anybody wants to make real-money bets, feel free to use the comment section on this post.
Appendix: Toy Models
In the course of the discussion, two simple models came up.
One model which I introduced, for equilibrium temperature: model the single-hose air conditioner as removing air from the room, and replacing with a mix of air at two temperatures: (the temperature of cold air coming from the air conditioner), and (the temperature outdoors). If we assume that is constant and that the cold and hot air are introduced in roughly 1:1 proportions (i.e. the flow rate from the exhaust is roughly equal to the flow rate from the cooling outlet), then we should end up with an equilibrium average temperature of . If we model the switch to two-hose as just turning off the stream of hot air, then the equilibrium average temperature should drop to . So, the two-hose system has double the equilibrium temperature delta of the one-hose system.
Note that the 1:1 flow rate assumption does a lot of work here, but I think it’s on the right order of magnitude based on seeing my single-hose air conditioner in action; if anything the exhaust blows more. The constant cold-temperature is more suspect.
Paul instead talked about efficiency, and claimed that
… the efficiency lost is roughly (outside temp—inside temp) / (exhaust temp—inside temp). And my guess was that exhaust temp is ~130.
I’m not sure how that formula was derived, but here’s my best guess. [EDIT: Paul summarizes his actual argument in this comment, and it makes much more sense than my guess below. Leaving the guess here for legibility, but it’s definitely not the calculation Paul did.]
In general, for an efficient air conditioner, the “efficiency” is , where:
is hot temperature, is cold temperature
is work required per unit of heat pumped
For the two-hose setup, there’s no downside to blowing lots and lots of outdoor air through the system, so the “hot” side of the heat pump can be kept at outdoor temperature. So, = (outside temp—inside temp)/(inside temp). But in the one-hose setup, the exhaust flow rate needs to be kept low to minimize infiltration losses, resulting in a higher exhaust temp. So, = (exhaust temp—inside temp)/(inside temp). Combine those two, and we get the ratio of work required to pump the same amount of heat in one-hose vs two-hose mode:
= (outside temp—inside temp)/(exhaust temp—inside temp)
… i.e. Paul’s formula. With outside temp 90°F/32.2°C, inside temp 80°F/26.7°C, and exhaust temp 130°F/54.4°C, this ratio would be around 20%.
… but that’s not a formula for efficiency lost. That formula is saying that two-hose takes only 20% as much energy as single-hose to pump the same amount of heat. The efficiency loss would be one minus that, i.e. around 80%. So my current best guess is that Paul found this formula, but accidentally used one minus efficiency loss rather than efficiency loss, and it just happened to match the 20-30% number he expected so he didn’t notice the error.
How realistic are the assumptions for this model? I think the two main problems are:
It’s not accounting for heat lost to infiltration; instead it’s assuming that exhaust flow is low enough to make infiltration loss small. I don’t think that’s realistic. Once we include infiltration losses, single-hose will need to pump more heat than two-hose in order to maintain the same temperature, whereas the ratio above is work required to pump the same amount of heat.
I doubt that exhaust in two-hose mode will be close to (especially for my experiment with a second hose attached to an air conditioner designed to operate with one hose, but also for ordinary two-hose air conditioners).
These two issues would push the error in opposite directions, though, so it’s not clear whether the 80% efficiency loss estimate is too high or too low.
- My AI Model Delta Compared To Christiano by (12 Jun 2024 18:19 UTC; 194 points)
- Air Conditioner Test Results & Discussion by (22 Jun 2022 22:26 UTC; 82 points)
- Proxy misspecification and the capabilities vs. value learning race by (16 May 2022 18:58 UTC; 23 points)
- 's comment on Shutting Down the Lightcone Offices by (15 Mar 2023 13:29 UTC; 2 points)


I said I was going to check out, but now there’s an entire new post with claims about my predictions and views. So I’m going to restate my predictions and views to avoid misrepresentation; interpret my last comment as merely checking of the previous discussion; interpret this comment as checking out of the new discussion; and try to keep myself to restating my views rather than saying anything new.
Clarifying predictions:
I said that the single-hose AC will be 25-30% less efficient when cooling from 90 to 80 degrees. That would mean the 2-hose AC has a temperature difference 33-43% larger. If there is a larger temp difference (and especially a higher outdoor temp) you will see a larger efficiency gap. You’d get to 50% if you were instead cooling from 97 to 80 degrees, or from 80 to 60 degrees (though that looks impossible in your test). These differences are measured for the 1-hose cooling.
Clarifying my calculation:
I estimated the efficiency loss at (outside temp—inside temp) / (exhaust temp—inside temp).
This was for constant exhaust temp. I agree that higher exhaust would would make a single-hose AC more inefficient, but it doesn’t seem related to Goodhart, since: (i) it is reflected in the BTU rating on the box, (ii) it is reflected in the temperature of air leaving the unit. So I don’t see how a consumer could be making a Goodhart-related mistake based on this type of inefficiency. It’s also not related to this experiment since it won’t be changed by adding a cardboard tube.
The reasoning was: at constant exhaust temp, each AC pays the same amount per unit of heat moved from the cool air to the hot air. But for each unit of air leaving the 1-hose unit, you have infiltration of the same quantity of hot air from the outside. This undoes some fraction of the work the AC did. What fraction? Well, each unit of exhaust moves C*(exhaust temp—inside temp) of heat outside. And each unit of infiltrated air brings C*(outside temp—inside temp) back. So you lose (outside temp—inside temp) / (exhaust temp—inside temp).
Reposting my final comment, which was left out of the summary:
There’s an important assumption being made here, which is that we care about temperature in the room with the air conditioner and the temperature in other rooms in the house equally. This assumption is false, especially in group-house situations.
I propose that two-hose air conditioners be referred to as type C air conditioners, and single-hose as type D. (Types A and B being hoseless in-window units and evaporative coolers, of course, as we would not wish to imply that anyone was defecting against their housemates.)
On the way home today, I was thinking about what kinds of AI strategies would look more promising in a world where people are more likely to actually notice problems—i.e. what kinds of strategies I’d invest more effort into if the air conditioner test (and things like it) surprises me.
One example strategy: make AI companies liable for problems caused by their AI, as much as possible. For example, if a programming AI generates a piece of code with a bug in it, and that bug causes some huge disaster for the company using the code, then the AI company should be liable for the damage. This will incentivize AI companies to fix problems before they reach production, rather than waiting on the (much slower) consumer feedback cycle.
Also, it will incentivize AI companies to build safety teams with actual teeth, rather than the kind of mostly-performative safety teams which regulations tend to create. In particular, that means tools to probe what the AI has learned and whether the AI has learned what it was supposed to learn.
In world where the important problems are hard to notice, I expect this to mostly not work—the incentive will mostly result in AIs which do bad things subtly enough that nobody ever notices and sues. But in a world where problems are generally noticed, liability would help a lot to align AI companies’ incentives.
‘Efficiency’ may be the wrong word for it, but Paul’s formula accurately describes what you might call the ‘infiltration tax’ for a energy-conserving/entropy-ignoring model: when you pump out heat proportional to (exhaust—indoor), heat proportional to (outdoor—indoor) infiltrates back in.
That’s an important argument, thank you.
Another test to consider is getting a two-hose AC unit, alternating whether the intake hose is attached to the window vs. free in the room (with the window blocked).
I’m confused about how one could modify a one-hose AC into a two-hose AC. If the one-hose model internally splits a single input into two outputs, it seems like this would require modifying the internal structure of the AC, rather than just taping on more hoses?
Good question! The split isn’t actually internal for my particular unit; there’s two separate intake vents on the outside.
Gosh, that practically sounds like it was designed to be modified in this way.
I’m most concerned about the engineering aspect and the weather.
Your jerry-rigged second tube may fail to convey outside air to the A/C effectively. It also may leak outside air into the room. In either case, I would expect these outcomes to mask, or even reverse, any efficiency benefits of the two-hose design.
It seems important to track the outside temperature to ensure that results are comparable across tests.
I’d suggest confirming that your thermometer(s) are reliable before running the A/C experiment.
I’m also not sure if endpoint temperature equilibration is the right call.
The concept for why the single-hose unit is bad is because it creates a heat input that counteracts the heat output, while the single-hose unit does not. As such, the rate of change of heat is reduced. This won’t necessarily result in a different equilibration temperature, however. Instead, I would expect it to affect the rate at which temperature equilibrates. I’m not 100% confident about this.
If A/C efficiency affects cooling rate rather than temperature equilibrium, then you have a degree of freedom in terms of deciding when to declare no appreciable change in temperature change. I think it would be good to preregister either an objective method for stopping a measurement, or a maximum time limit on waiting for equilibration.
It seems easy to track the time it takes to equilibrate, so why not report these outcomes as well?
Sincerely,
Reviewer #2
I expect conveyance issues to be handled well by just making the tube big. If we use a Poiseuille flow approximation, throughput scales like R^4. I was planning to use boxes with ~1ft square cross section, compared to the 6-inch diameter of the air conditioner’s hose, so my jerry-rigged second tube should have over 10X the capacity of the output hose even after some inefficiency.
(That might not work if we’re in a regime where boundary layer effects dominate, but in that regime I expect there will be plenty of airflow regardless. Also, the Darcy-Weisbach equation says R^4 is a good empirical approximation regardless.)
That still leaves turbulence in the corners as a potential issue, but I only plan to have two corners, and hopefully just making things big will also minimize corner issues.
I do plan to check for leaks by running my hand around to feel for airflow. Leaks small enough to not be caught by that method are probably small enough that they won’t impact the results much. (Note that the probable direction of a leak would not be to leak outside air into the room, but rather to leak inside air into the cardboard intake tube. It’s an intake tube, after all, so it should have slightly negative pressure compared to the room.)
I do plan to measure outside temperature, though I expect it’s fine if there’s some outdoor temperature difference between the tests. The tests are looking at temperature delta relative to outdoor temperature, so I just need to have an outdoor temperature measurement taken at roughly the same time as the indoor measurements for each test condition.
Any particular suggested calibration method? I do have at least two different thermometers to compare against each other.
My guess is calibration won’t matter much, so long as I use a single thermometer for all the measurements, so it doesn’t need to be perfect.
Remember, the thing we really want to test is whether single-hose air conditioners yield bad outcomes for consumers. Temperature equilibrium is what I most cared about as a consumer.
I doubt the speed to equilibrate will be significantly different, but it makes sense to report it regardless.
When the change over 15 minutes is less than the uncertainty in my measurements (e.g. thermometer precision or retest discrepancy, whichever is larger), I’ll call that an equilibrium.
I’m also worried about the cardboard hose failing.
My impression was that these two things are necessarily linked, in a fairly direct fashion.
Equilibrium means that increases and decreases cancel out. In the absence of an AC, the rate at which heat enters a given building is proportional to the difference between interior and exterior temperature. Therefore, the maximum temperature delta that an AC can maintain should be directly proportional to how quickly it can pump (net) heat out.
I mean, you could choose to think about infiltration as an intensified pressure towards equilibrium instead of as a decrease in the net effectiveness of the pump, and then equilibrium temperature would cease to be a good measure of “pump effectiveness”. But that would effectively be asking to have the one-hose design not be penalized for the infiltration losses that it directly causes.
EDIT: Addendum: Notice that the rate at which the one-hose AC will pump (net) heat out depends on the temperature delta. (Replacing inside air with outside air doesn’t matter if they’re the same temperature, but it matters a lot if there’s a large temperature difference.) So “the rate of change of heat” isn’t actually well-defined until you’ve specified what temperature delta you’re measuring at. (Which is why it’s possible to invent formulas for the official efficiency stats that would favor or disfavor one-hose models.)
I think you’re mostly right? But if both pumps have an equilibration temperature below 60 degrees, then we can only get their efficiency difference by looking at the cooling rate. Perhaps if this is the case, we are saying that there just isn’t a difference from the point of view of this experiment.
On the other hand, my impression is that efficiency ratings are mostly supposed to be about how much energy it takes to reach a given equilibrium. So I’m not sure if this experiment is really a referendum on the claimed differences between AC units. We can imagine that both AC types could get the house equally cold, but one-hose units use a lot more energy. From the perspective of equilibrium temps, there’s no difference, but from the perspective of efficiency ratings there is!
Since the point of the experiment is to determine the adequacy of AC ratings as a proxy for AI issues, it seems like you’d want to focus on efficiency rather than equilibrium temperature.
...I’m going to try making a point that would be generally unacceptable to make in wider Internet culture, but which I think will be considered acceptable on LessWrong. Apologies if I miss.
Meta observation: You’ve just made several points that seem connected to the OP, but not to anything that I said, and in so doing have quickly earned a karma higher than any other comment in this particular comment chain. This seems like a warning sign for arguments as soldiers (i.e. you’re treating any point about the larger topic as being substitutable into a discussion about a narrow sub-topic, and earning more karma because there are a larger number of people who care about the larger topic than the smaller one).
Also, both of the topics you just raised (possible equilibrium below 60 degrees and electrical efficiency vs maximum cooling) are things that were mentioned in the OP. I feel that, ideally, discussion of them should acknowledge and respond to the OP’s position on these points instead of raising them as if they were new.
I think it’s fine to sidebar about this. If you didn’t know, you can hover over the karma indicator on a comment or post to see how many people have voted on it. In the case of my comment, only 1 person (gbear) has voted on it at the time of writing.
However, I’m not sure about the point you’re making.
This quote suggests that you prefer a norm that comment responses be carefully focused on the specific topic raised by the comment. While that is reasonable, it is also a reasonable norm to use comments in an open-ended fashion to better understand the main topic at hand.
I lean heavily on the latter norm, partly because I tend to do a lot of my thinking out loud. This comes out in my comments. My internal experience is that I was thinking out loud about the experiment, taking into the point you raised, without carefully checking to see if John had raised the issue already. That to me is not “soldier mindset,” but I could be criticized as just adding noise to the discussion, as you suggest at the bottom of your comment.
This might be true, but I think this is a lot of analysis for a phenomenon of minor overall importance with limited evidence. Consider that I could respond by suggesting that your comment here, a complete diversion from the topic of ACs, is transparently a reaction to perceiving yourself to be getting less karma than me, and much more in keeping with a “soldier” mentality than anything I did in my preceding comment.
I don’t actually want to accuse you of that, because I do think that the social dynamics of commenting is interesting. According to the norm I described above, I think it’s fine to divert in most cases.
I’ve written a couple posts on commenting norms on LW, and others have brought up the topic as well. Since you seem to have thoughts along these lines, it might be worth branching off a separate post comparing the pros and cons of some alternatives for community consideration.
Upvoted both this and the parent comment for doing a good job discussing a notoriously flamey topic politely and with cool heads. Good job both of you.
Cheers!
Thanks
I may have over-emphasized the “higher karma” thing. I don’t consider that a warning flag in itself; higher karma further down the thread can happen for various perfectly valid reasons. I consider it a minor supporting point because it seems correlated with a particular pattern I’ve noticed on other sites (mainly reddit).
And apparently I underestimated the degree to which it’s possible for a single voter to generate high karma on LessWrong, so I hereby retract that as supporting evidence.
I entirely believe you that your subjective experience was that you read my comment, thought about how it related to the larger topic, generated some new thoughts, and then posted those. I’m not trying to take a stand against that in general, but I’m concerned about the specific relationship between my comment and your follow-up thoughts, and why/how the one prompted the other.
(Maybe pause here for a moment to think about that, and form your own hypothesis about why my comment sent your thoughts in that particular direction.)
It looks to me like things unfolded something like this:
You read the OP, thought about it, and (I suspect) put some effort into making a list of all the relevant things that occurred to you. One of the things in that list was a concern that the experimental endpoint may be bad because of reason X.
I explained why X was not a concern.
You responded that the experimental endpoint may be bad because of reasons Y and Z.
It looks to me like the connection between my comment and your new thoughts is that the new thoughts are new reasons to continue believing what you already believed. Interesting that my comment would suddenly cause you to think of those? (Whereas reading the OP, which explicitly talked about Y and Z, did not make you think of them.)
(As I write this, it occurs to me that what I’m doing in this very post looks kind of similar: I am giving an explanation for objecting to your comment that is not identical to the reason I gave before. Subjectively, this feels like putting my thoughts into a more coherent order so that I have a stronger grasp on my earlier feelings. But perhaps I’m rationalizing? Or, alternately, perhaps I’m not extending enough benefit-of-the-doubt to you? Does this post feel to you like a clarification of my previous reasons or like a new reason?)
I think that Y and Z are legitimate discussion points within the broader context of the experiment but bringing them up in this particular way kind of feels like an attempt to avoid updating.
And I suppose I’m also feeling a bit awkward because I defended the experimental setup against X, and now this conversation flow makes me feel somehow vaguely obligated to also defend the experimental setup against Y and Z (or else “concede” Y and Z) when, in fact, I don’t necessarily have any opinions about the new arguments one way or the other. I’m definitely not saying that’s a reasonable emotional response on my part, yet it also feels like a somewhat predictable result of this conversational pattern where I objected to the local validity of one argument and you responded with unrelated arguments for the same conclusion.
I’d frame my approach to both reading and commenting as “iterative reading.” I read to a certain level of depth, write up thoughts that seem pertinent, and then reread and redirect my attention in response to other people’s replies.
Even for my actual research in grad school, this is inevitable. There’s simply too much information to take it all in and retain it; most is unimportant. This is even more true in responding to a blog post about somebody else’s research.
I look at my comments as trying to provide some value. If they’re wrong, hopefully I’ll be corrected. If they’re redundant, I’ll be ignored. If they’re right, then I contribute a bit. Plus, writing up my thoughts helps me remember and understand more, and the pushback from others helps me stay engaged and to focus on the specific areas where my understanding is incomplete.
In this approach, commenting is more about contributing and learning.
There are other places where I’ve approached commenting with a focus on evaluating an argument. For example, my post the other day about “how to place a bet on the end of the world” led to comments that significantly shifted my view, which is a thought process I recorded in the comments to the post.
So I guess I view your argument as standing on its own. It seems correct to me, but I also am not completely certain, and don’t care to investigate further. But it also does provoke consideration of how much of the point I was making needs to be updated. That’s what I tried to articulate in the subsequent comment.
I think the takeaway here is that there’s a difference between the “learning and contributing to a project” style and the “evaluating an argument” style. Which of course is about emphasis, it’s not a rigid binary.
I had difficulty translating your comments and my thoughts into a mutually-compatible frame so that I could understand how they bear on each other. Could I get your feedback on this translation attempt?
It seems like you have a model for your commenting behavior that looks something like:
You read a piece.
This generates too much mental work for you to do it in one sitting, so you queue some of it to happen later.
In the mean time, you post comments based on the portion of the mental work you’ve completed so far.
In this case, when you read my reply, this refocused your attention on the general topic and caused you to do another chunk of already-queued work (with the subject of my comment maybe influencing which part of the work you focused on).
Completing this queued mental work generated new thoughts.
You posted these new thoughts as a reply to my comment because my comment triggered them, but you were always going to generate approximately those thoughts when you got around to your queued mental labor, regardless of what I posted.
And then this relates to the points I raised as follows:
My concern could be rephrased as: Generating unrelated arguments for the same side is a likely outcome for someone in a soldier mindset, and unlikely for a curious exploration of the specific argument being discussed. This outcome is therefore Bayesian evidence for soldier-mindset.
According to your model, you’re not doing either of those things; you are instead doing curious exploration of the original post, which was merely prompted by my comment.
Generating these new arguments is not a particularly unlikely outcome for curious exploration of the original post, so it doesn’t lose nearly as much probability from this particular piece of evidence.
Given your strong prior on your existing model, your posterior probability for it is still pretty high.
Does this seem like an accurate translation to you?
Point of order: I don’t think “arguments as soldiers” was supposed to be equivalent to “thinking of multiple different ideas for why something would not work”—it was about a lack of intellectual integrity in honestly viewing the opponent’s points on their merits, and simultaneously pretending their are no weaknesses in your own arguments.
Good debate requires adversarial thought, which is why we talk about Steelmanning instead of Strawmanning.
If AllAmericanBreakfast has generated even half a dozen different, seemingly unrelated ideas for why the the OP’s experiment does not measure the value it claims to be studying, that still doesn’t immediately make them a soldier. They’d also need to ignore criticism of the arguments, and ignore opposing arguments or attack the opposing arguments in a way that is hypocritical of how they treat their own arguments.
I view this pivot to focus on how someone generates their ideas (what you called “a model for commenting behavior”) as a far more troublesome road.
If we’re going to dismiss arguments because we think the intellectual process to generate them was invalid, that’s an actual “argument as soldiers” mindset in my opinion because it is diverting attention from the argument itself to a process objection instead.
In other words, if AllAmericanBreakfast had raised an important and critical point that up until now was missed, would it be rational to dismiss it because it was posted as an off-the-cuff reply after talking a walk outside, instead of only after some period of careful examination that one is expected to spend their time in prior to commenting on a new post?
I largely agree with you. Steelmanning, a focus on the object-level argument rather than the meta-process, and a certain graciousness about the messiness of intellectual labor are all helpful in promoting good debate.
If I had to guess, Dweomite might have gotten a “Gish gallop” vibe, in which every rebuttal leads to two new bjections being raised, with scarcely an acknowledgement of the rebuttal itself. Part of the art of good debate is focusing attention in a productive manner. Infodumps and Gish gallops can be counterproductive, even if the object-level information they contain is correct.
It was never my intention to equate “arguments as soldiers” with “multiple arguments for the same conclusion”, or to say that having multiple arguments is inherently bad. That’s why I described this as being (in context) a warning sign, not an error in itself.
It was also never my intention to dismiss these particular arguments. I believe I said above that they seem like valid discussion points. But my interests are not confined solely to the AC experiment; I am also interested in the meta-project of improving our tools for rationality.
(Though I can imagine some situations where I would dismiss arguments based on how they were generated. For instance, if I somehow knew that you had literally rolled dice to choose words off of a list with no regard for semantic content, and then posted the output with no filtering, then I would not feel that either rationality or fairness required me to entertain those arguments.)
.
That said, I think you also got a rather different take-away from “arguments as soldiers” than I did. I see it as being about goals, not rules of conduct. If you identify with a particular side, and try to make that side win, then you’re in a soldier mindset. If, while you do that, you also feel a duty to acknowledge the opponent’s valid points and to be honest about your side’s flaws, then you’re a soldier with rules of engagement, but you’re still a soldier.
The alternative is curiosity and truth-seeking. If your goal is to find the truth, then acknowledging someone else’s valid point isn’t a mere duty, it’s good strategy.
You wrote: “Good debate requires adversarial thought”. I might or might not agree, depending on how you define “debate”. But regardless, adversarial thought is NOT a requirement for truth-seeking. You can investigate, share information, and teach others, and even resolve factual agreements without it.
For instance, Double Crux is a strategy for resolving disagreements that doesn’t rely on adversarial thought. I’m also reminded of Aumann-style consensus.
Rules of engagement are certainly better than nothing. Thus is it written:
But duties are not what you’re ideally hoping for.
That seems about right :)
Thank you. If I add your model to my hypothesis space, the probability on soldier-mindset does seem a lot less worrying.
I also now feel like I understand why you initially tried to frame this as a disagreement about posting etiquette. Posting the output of your queued work as a reply to a comment that refocused your attention (but is otherwise unrelated) seems weird to me.
It seems like you’re desiring a sort of Kialo-like approach to commenting, in which each comment chain is tackling an ever-more-narrow subargument. This does seem to be how some comment chains progress, and it would probably make for more legible reading. In the case of the comment you objected to, I could have said “I think you’re right,” realized the rest of my commentary could be split off into a separate comment, and then we wouldn’t have had an issue.
There’s something about the perception of being involved in a conversation with another person that keeps my attention anchored on the range of topics associated with that conversation. But rather than being ever-more-narrowly focused on the most recent reply, my attention fans out throughout the available text.
For example, in writing this comment, I find myself considering not only commenting etiquette, but also re-reading my original comment and your reply, and considering why I didn’t find your reply 100% convincing (instead saying “I think you’re mostly right”).
Then I start typing those thoughts, because the cursor’s in the text box. It would be inconvenient to split off AC-relevant thoughts into a different comment. It also feels weirder to me to make lots of comments on different subtopics than one long comment with all my thoughts. But in this case, I’m also paying enough attention to notice that most of these thoughts are not immediately relevant to this sub-topic, and delete them.
If I don’t edit my own comments to exclude thoughts that aren’t relevant to the subtopic under immediate discussion, all my thoughts at a particular moment in time tend to wind up in the same comment.
I suspect this habit comes from verbal debate, in which there isn’t really a convenient way to separate out thoughts into subtopics, and where a thought not verbalized can easily be forgotten.
I don’t think your description of what I want is entirely accurate. I wouldn’t say that I expect sub-comments to never be wider than their parent, but I expect that they’re somehow a response to the parent, rather than just being whatever you happened to be thinking about at the moment you wrote the sub-comment.
For example, if I posted an analogy about how air conditioners are somehow like kittens, then all of these would seem like reasonable responses that could be considered to widen the topic:
I think air conditioners are more like jellyfish because (reasons)
I’ve long thought that alarm clocks are similar to kittens for largely similar reasons; perhaps there’s an unexplored connection between air conditioners and alarm clocks?
That analogy makes sense, but it doesn’t address X, which seems to me like an important consideration
But it seems disconnected to me to post something like:
My cat just had a litter of kittens and I’m trying to find homes for them; anyone want one?
This summer is so hot. I really wish I had a better air conditioner right now.
It’s understandable that you would think of those things right after reading my hypothetical comment, but they’re not really responses to it.
I agree spoken conversations need somewhat different rules; however, even in spoken conversations there’s some etiquette limiting when and how you can change the topic of discussion.
Unfortunately, I don’t think the lines between a direct response to a comment and a non-response are clear. My reply to your comment wasn’t unrelated to your response. It just wasn’t as carefully focused as you desired.
I’ll also say that, no matter what rules we might come up with for commenting, at the end of the day the ability to coordinate around those rules, and people’s mental budget for following them, will dictate how conversation flows. At this point, I feel that this conversation has shifted from feeing like an exploration of commenting norms using our exchange as an example, and begun to feel like an evaluation of the adequacy of my commenting behavior. The latter is not really something I’m interested in.
I agree my line isn’t particularly sharp. This is less of a considered policy and more an attempt to articulate my intuitions.
Ending the discussion would be fair.
I’m glad I eventually understood your commenting model, though. I don’t feel like I often have opportunities to explore conflicts of expectations in detail, so this was valuable evidence for updating my overall Internet-discussions-model. (As well as a reminder that other peoples’ frames are both harder to predict and harder to communicate than my intuitions would suggest.) So thanks.
I strong upvoted AllAmericanBreakfast’s comment, so the high relative karma is entirely my fault. I basically strong upvoted because it felt right to me, not thinking about how much karma the other comments in the chain had, so I’m sorry that it didn’t match your assumptions about how karma in threads should work. I don’t think that I’m behaving in an arguments-as-soldiers way, but that’s difficult to prove to myself, let alone to another person.
This is the reasoning that I had, but I’m not strongly attached to it: Thinking to the original post about takeoff/air conditioning, the original discussion was about whether an AC unit is useful to the consumer, which means that it achieves the goal of an air conditioned room in a reasonable length of time without being wasteful or expensive. In my experience, AC units generally can achieve their goal of an air conditioned room, so it seems likely that the considerations from the OP ([0], [1]) aren’t helpful and the tests won’t achieve the purpose from the original post. Even if the AC is not able to air condition the room to an arbitrary point (perhaps OP’s room has a lot of glass windows or is poorly insulated), it seems like it will be measuring the wrong things and that OP didn’t fully consider them.
[0]: “I am assuming that the AC runs continuously (as opposed to getting the room down to target temperature easily, at which point it will shut off until the temperature goes back up). If that’s not the case, I will consider the test invalid, and retry on a hotter day.”
[1]: “Equilibrium indoor temperature was the main thing I cared about when using this air conditioner; electricity is relatively cheap”
Do the people disagreeing with your other post really want to buy the whole analogy, but disagree with the evaluation wrt air conditioners?? I would have guessed they merely selected an easy-looking nitpick to start with?
Or on the other hand, do they really buy the whole argument that this is a good way to test what kinds of problems wrt AGI we can expect the market to address, not merely an illustration of said argument, and therefore that the best way to settle the dispute is to specifically debate the point wrt air conditioners rather than, say, try for a representative market sample of potential problems fitting various patterns, and whether those problems naturally get solved by the market or not?
… Or am I reading too much into this and people just want to talk about AC?
I viewed this as nitpicking a claim that’s not super central. It felt indicative of a general pattern amongst rationalists of overconfident/overstated claims about civilizational inadequacy. I think often there are real problems in these cases, but they are kind of messy and typically not as big a deal as claimed.
I think it only has relevance to my views about AI alignment insofar as civilizational inadequacy is also relevant there. I don’t think the detailed claims about AC have much relevance to the general story about civilizational inadequacy but I agree they have some. I don’t think the prediction in this post has that much relevance to whether the OP was overstated but I agree it has some.
In my original comment I made a prediction for the OP that amounted to predicting a 33-43% difference for typical use. John is predicting a >50% difference under some particular conditions that look likely to be pretty similar to that. The reader can decide how significant that is.
Makes sense.
I do think there’s something sort of like a silent evidence problem for civilizational inadequacy. Something resembling green rationalists. There’s a natural tendency for claims of inadequacy to offend someone, because there’s a claim that someone is doing something wrong. As a result, there’s a natural tendency for evidence and arguments for inadequacy to soften as they get passed along the social web. A tendency to preferentially fill in excuses rather than condemnations.
Self-consciousness wants to make everything about itself. It’s like the parable of the gullible king.
So I have a tendency to pay more attention to the pro-inadequacy pieces of evidence that make it to me, because I think they’re probably more like what the real world looks like under the hood, and somewhat ignore arguments to the effect that they’re not as big a failure as they first appear.
But such reasoning should be employed cautiously.
I think there’s a real disagreement between worldviews upstream of both air conditioners and alignment, and the AC thing is a real test between those worldviews. It wasn’t chosen to be a particularly optimal test, but finding good clean disagreements between worldviews does take some work and this opportunity just kind of dropped in front of us on a silver platter.
I’ll be performing a (modest) update on the results of this experiment, and I strongly endorse John’s comment here as an explanation of why—it’s testing a worldview that’s upstream of both this AC debate and alignment.
In my case, the worldview being tested isn’t about civilizational inadequacy. Rather, it’s about how likely optimizers (e.g. the market, an AI system) are to do things that seem to satisfy our preferences (but actually have hidden bad side effects that we’re not smart enough to notice) vs. do things that actually satisfy our preferences. In other words, I’m interested in the question of whether optimizers will inevitably learn to Goodhart their objective function, including in cases of rich objective functions like “consumer satisfaction.”
I also strongly agree with John’s framing as this being just one bit of evidence, and not enough evidence to be a full crux. Really drilling down into this point would look more like selecting lots of top-rated goods and services and trying hard to figure out how many of them cause significant side-effects that don’t seem to be priced into consumers’ opinions.
Is it a crux for you? It feels to me like it shouldn’t be a crux for you.
You mean the AC thing? If I’m wrong, it wouldn’t be enough bits to flip all the relevant parts of my alignment views, but it would be enough bits that I’d be a lot less certain and invest more in finding other ways to gain bits.
(Though obviously that depends somewhat on how I turn out to be wrong.)
Yeah, sounds about right.
I feel like I’d think less of John if it weren’t a crux for him? Like, one of the troubles with worldviews like this is they lean both on your theories and on your evidence, and so you really need to grab at the examples that do shine thru of “oh, my worldview found this belief of mine very confirming, but people disagree with it; we should figure out whether or not I’m right.”
I think it makes sense to have a loose probabilistic relationship. I do not think it makes sense for it to be a crux, in the sense of a thing which, if false, would make John abandon his view. There are just too many weak steps. The AI industry is not the AC industry. I happen to agree with John’s views about AC, but it’s not obvious to me that those views imply this particular test turning out as he’s predicting. (Is he averaging over the wrong points?) It’s more probable than not, but my point here is that the whole thing is made of fairly weak inferences.
To be clear, I am pro what John is doing and how he is engaging; it’s more John’s commentors who felt confusing to me.
I will personally be updating my priors depending on the results of this test. If it turns out that the AC is actually bad at its job, I will very slightly update towards being pessimistic about us catching failure modes of AGI before it’s too late. If, however, it turns out that it does not make a substantial difference, I will somewhat more strongly (though not very strongly) update towards being more concerned about us missing these sorts of things. One question I’m not sure how to answer is how (if at all) I should update based on the seemingly obvious cherry-picked example not being obvious at all.
For the record I have never personally bought an AC and am interested in getting a good recommendation soon :)
The argument as presented is:
System failures exist
Here is one example of a system failure
And the counterargument is: No, 2 is not an example of a system failure Therefore, I am not updating my prior for 1. because no new evidence has been presented
Do I understand correctly that your makeshift second hose will connect the outside air to the “hot” path of the AC inlet stream? Will you be able to extend the divider to entirely isolate it from the “cold” path? Not sure about the exact details of your model, but if, for example, there is a single blower fan pulling air into the inlet before splitting it into hot and cold paths, then you won’t be able to maintain separation and outside air from your second hose will mix with inside air in the blower before being separated again.
There’s two separate blower fans and two separate intake vents on my particular unit.
I’m on vacation right now so I haven’t made any concrete plans, but I’m reasonably interested in making this happen slash I’m interested in figuring out a specification for a bounty that would cause someone else to do science and empiricism on this.
I’ll say now that I’d probably be happy to cover all costs plus pay $1k+ for someone to do a fairly thorough comparison between this model and others with two valves. I haven’t figured out the details for it yet, but if you think you’d be down to do a good job with this and are willing at around this price range, please PM me.
Also, I would love to get someone to do this experiment who doesn’t have the context of the original post, doesn’t know what’s being debated, and just is given the task of reporting the effectiveness of a few AC machines. Probably this is doable but not by a LessWrong reader.
I have a friend who is not in the community that I’m fairly certain would be willing to test this independently for a $2/3k bounty. I will be offline Friday and Saturday, but DM me with details and I can pass them along on Saturday night/Sunday.
I would be willing to pay for this. Will DM you.
Where will the air conditioner be drawing its excess air from, in the one-hose case? if it’s indoors but outside the bedroom, what are your assumptions about the temperature there?
It’s pretty easy to get that data if you want it. $14 on amazon
https://www.amazon.com/Electricity-Monitor-Voltage-Overload-Protection/dp/B07DPJ3RGB
Will your improvised intake tube cause your room to become positive pressure? It sounds like your “two hose” AC setup will pump in outside air, split it into a hot and cold stream, then dump the hot outside and the cold inside. If so you’re not replicating two-hose efficiency, since you’ll be pushing cold air out of your room!
My particular AC has two separate intake vents, so this shouldn’t be an issue.
Ah, nice!
Just curious, why did you personally buy a one-hose AC unit in 2019 rather than two-hose?
I didn’t realize one-hose units were even a thing. I was very confused when I opened the box and there was only one hose.