Timeless Physics

[Eliezer Yudkowsky]

Previously in series: Relative Configuration Space

Warning: The central idea in today’s post is taken seriously by serious physicists; but it is not experimentally proven and is not taught as standard physics.

Today’s post draws heavily on the work of the physicist Julian Barbour, and contains diagrams stolen and/​or modified from his book “The End of Time”. However, some of the arguments here are of my own devising, and Barbour might(?) not agree with them.

I shall begin by asking a incredibly deep question:

What time is it?

If you have the excellent habit of giving obvious answers to obvious questions, you will answer, “It is now 7:30pm [or whatever].”

How do you know?

“I know because I looked at the clock on my computer monitor.”

Well, suppose I hacked into your computer and changed the clock. Would it then be a different time?

“No,” you reply.

How do you know?

“Because I once used the ‘Set Date and Time’ facility on my computer to try and make it be the 22nd century, but it didn’t work.”

Ah. And how do you know that it didn’t work?

“Because,” you say, “I looked outside, and the buildings were still made of brick and wood and steel, rather than having been replaced by the gleaming crystal of diamondoid nanotechnological constructions; and gasoline was still only $4/​gallon.”

You have… interesting… expectations for the 22nd century; but let’s not go into that. Suppose I replaced the buildings outside your home with confections of crystal, and raised the price of gas; then would it be 100 years later?

“No,” you say, “I could look up at the night sky, and see the planets in roughly the same position as yesterday’s night; with a powerful telescope I could measure the positions of the stars as they very slowly drift, relative to the Sun, and observe the rotation of distant galaxies. In these ways I would know exactly how much time had passed, no matter what you did here on Earth.”

Ah. And suppose I snapped my fingers and caused all the stars and galaxies to move into the appropriate positions for 2108?

“You’d be arrested for violating the laws of physics.”

But suppose I did it anyway.

“Then, still, 100 years would not have passed.”

How would you know they had not passed?

“Because I would remember that, one night before, it had still been 2008. Though, realistically speaking, I would think it more likely that it was my memory at fault, not the galaxies.”

Now suppose I snapped my fingers, and caused all the atoms in the universe to move into positions that would be appropriate for (one probable quantum branch) of 2108. Even the atoms in your brain.

Think carefully before you say, “It would still really be 2008.” For does this belief of yours, have any observable consequences left? Or is it an epiphenomenon of your model of physics? Where is stored the fact that it is ‘still 2008’? Can I snap my fingers one last time, and alter this last variable, and cause it to really be 2108?

Is it possible that Cthulhu could snap Its tentacles, and cause time for the whole universe to be suspended for exactly 10 million years, and then resume? How would anyone ever detect what had just happened?

A global suspension of time may seem imaginable, in the same way that it seems imaginable that you could “move all the matter in the whole universe ten meters to the left”. To visualize the universe moving ten meters to the left, you imagine a little swirling ball of galaxies, and then it jerks leftward. Similarly, to imagine time stopping, you visualize a swirling ball of galaxies, and then it stops swirling, and hangs motionless for a while, and then starts up again.

But the sensation of passing time, in your visualization, is provided by your own mind’s eye outside the system. You go on thinking, your brain’s neurons firing, while, in your imagination, the swirling ball of galaxies stays motionless.

When you imagine the universe moving ten meters to the left, you are imagining motion relative to your mind’s eye outside the universe. In the same way, when you imagine time stopping, you are imagining a motionless universe, frozen relative to a still-moving clock hidden outside: your own mind, counting the seconds of the freeze.

But what would it mean for 10 million “years” to pass, if motion everywhere had been suspended?

Does it make sense to say that the global rate of motion could slow down, or speed up, over the whole universe at once—so that all the particles arrive at the same final configuration, in twice as much time, or half as much time? You couldn’t measure it with any clock, because the ticking of the clock would slow down too.

Do not say, “I could not detect it; therefore, who knows, it might happen every day.”

Say rather, “I could not detect it, nor could anyone detect it even in principle, nor would any physical relation be affected except this one thing called ‘the global rate of motion’. Therefore, I wonder what the phrase ‘global rate of motion’ really means.”

All of that was a line of argument of Julian Barbour’s, more or less, Let us pause here, and consider a second line of argument, this one my own. That is, I don’t think it was in Barbour’s The End of Time. (If I recall correctly, I reasoned thus even before I read Barbour, while I was coming up with my unpublished general decision theory of Newcomblike problems. Of course that does not mean the argument is novel; I have no idea whether it is novel. But if my argument is wrong, I do not want it blamed on an innocent bystander.) So:

“The future changes as we stand here, else we are the game pieces of the gods, not their heirs, as we have been promised.”
—Raistlin Majere

A fine sentiment; but what does it mean to change the future?

Suppose I have a lamp, with an old-style compact fluorescent bulb that takes a few seconds to warm up. At 7:00am, the lamp is off. At 7:01am, I flip the switch; the lamp flickers for a few moments, then begins to warm up. At 7:02am, the lamp is fully bright. Between 7:00am and 7:02am, the lamp changed from OFF to ON. This, certainly, is a change; but it is a change over time.

Change implies difference; difference implies comparison. Here, the two values being compared are (1) the state of “the lamp at 7:00am”, which is OFF, and (2) the state of “the lamp at 7:02am”, which is ON. So we say “the lamp” has changed from one time to another. At 7:00am, you wander by, and see the lamp is OFF; at 7:02am, you wander by, and see the lamp is ON.

But have you ever seen the future change from one time to another? Have you wandered by a lamp at exactly 7:02am, and seen that it is OFF; then, a bit later, looked in again on the “the lamp at exactly 7:02am”, and discovered that it is now ON?

Naturally, we often feel like we are “changing the future”. Logging on to your online bank account, you discover that your credit card bill comes due tomorrow, and, for some reason, has not been paid automatically. Imagining the future-by-default—extrapolating out the world as it would be without any further actions—you see that the bill not being paid, and interest charges accruing on your credit card. So you pay the bill online. And now, imagining tomorrow, it seems to you that the interest charges will not occur. So at 1:00pm, you imagined a future in which your credit card accrued interest charges, and at 1:02pm, you imagined a future in which it did not. And so your imagination of the future changed, from one time to another.

As I remarked previously: The way a belief feels from inside, is that you seem to be looking straight at reality. When it actually seems that you’re looking at a belief, as such, you are really experiencing a belief about your beliefs.

When your extrapolation of the future changes, from one time to another, it feels like the future itself is changing. Yet you have never seen the future change. When you actually get to the future, you only ever see one outcome.

How could a single moment of time, change from one time to another?

I am not going to go into “free will” in today’s blog post. Except to remark that if you have been reading Overcoming Bias all this time, and you are currently agonizing about whether or not you really have free will, instead of trying to understand where your own mind has become confused and generated an impossible question, you should probably go back and read it all again. For anyone who is just now joining us… perhaps I shall discuss the issue tomorrow.

Just remember Egan’s Law: It all adds up to normality. Apples didn’t stop falling when Einstein disproved Newton’s theory of gravity, and anyone who jumped off a cliff would still go splat. Perhaps Time turns out to work differently than you thought; but tomorrow still lies ahead of you, and your choices, and their consequences. I wouldn’t advise reworking your moral philosophy based on confusing arguments and strange-seeming physics, until the physics stops appearing strange and the arguments no longer seem confusing.

Now to physics we turn; and here I resume drawing my ideas from Julian Barbour.

For the benefit of anyone who hasn’t followed the series on quantum mechanics, a very very quick summary:

• In classical physics—the mistaken physics that was developed first historically, and matches human intuitions all too well—a particle is like a little billiard ball. A particle is in a single place in 3D space, and we can describe its position with three real numbers. In quantum physics, we need an amplitude distribution over all possible positions for the particle—a complex number for the particle being here, a complex number for the particle being there, and so on through all the positions in space; a continuous distribution. (Configurations and Amplitude.)

• In classical physics, we can consider each particle independently. This particle is here, that particle is there. In quantum physics this is not possible; we can only assign amplitudes to configurations that describe the simultaneous positions of many particles. In fact, the only mathematical entities that actually have amplitudes are joint configurations of all the particles in the entire universe. (Joint Configurations.)

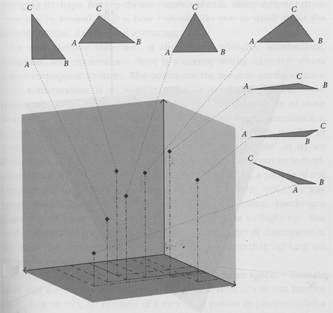
Above is a diagram that shows what a configuration space might look like for three particles, A, B, and C. ABC form a triangle in two-dimensional space. Every individual point in the configuration space corresponds to a simultaneous position of all the particles—above we see points that correspond to particular triangles i.e. joint positions of A, B, and C. (Classical Configuration Spaces; The Quantum Arena.)

The state of a quantum system is not a single point in this space; it is a distribution over this space. You could imagine it as a cloud, or a blob, or a colored mist within the space.

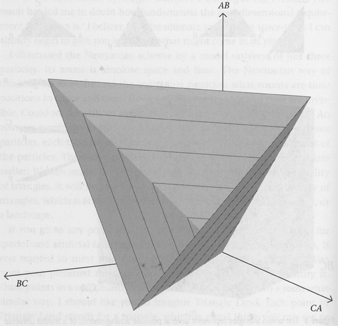
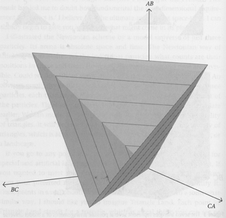
Here we see a relative configuration space, in which each axis is the distance between a pair of particles. This has some advantages I’m not going to recapitulate (it was covered in a previous post), so if you’re dropping into the middle of the series, just pretend it’s a regular configuration space.

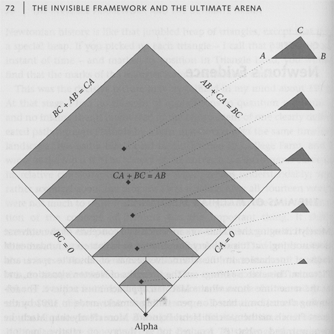
We’ve just chopped up the pyramidal space you saw before, into a series of slices. In this configuration space, the slices near the bottom show all the particles close together (tiny triangles). As we rise up, the particles get further apart (larger triangles).

At the very bottom of the configuration space is a configuration where all the particles occupy the same position.

(But remember, it’s nonsense to talk about an individual particle being anywhere in a configuration space—each point in the configuration space corresponds to a position of all the particles. Configuration space is not the 3D space you know. It’s not that there are a bunch of particles resting in the same place at the bottom. The single bottom point corresponds to all the particles being in the same place in 3D space.)

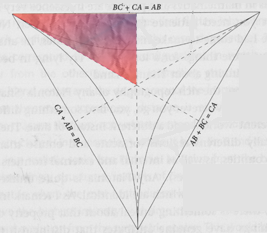
Here we take a closer look at one of the slices of configuration space, and see a cloud of blue and red mist covering some of it. (Why am I only showing the cloud covering a sixth (exactly a sixth) of the triangle? This has to do with a symmetry in the space—exchanges of identical particles—which is not important to the present discussion.)

But there is your glimpse of some quantum mist—in two colors, because amplitudes are complex numbers with a real and imaginary part. An amplitude distribution or “wavefunction” assigns a complex number to every point in the continuous configuration space—a complex number to every possible configuration of all the particles.

Yesterday, I finished by asking how the state of a quantum system might evolve over time.

You might be tempted to visualize the mist churning and changing colors, as quantum amplitude flows within the configuration space.

And this is indeed the way that you would visualize standard physics.

Behold the standard Schrödinger Equation:

Here ψ(r, t) is the amplitude distribution over configuration space (r) and time (t). The left-hand side of the Schrödinger Equation is the change over time of the wavefunction ψ, and the right-hand-side shows how to calculate this change as the sum of two terms: The gradient of the wavefunction over configuration space (at that time), and the potential energy of each configuration.

Which is to say, the derivative in time of the wavefunction—the instantaneous rate of change—can be in terms of the wavefunction’s derivative in space, plus a term for the potential energy.

If you tried to visualize Schrödinger’s Equation—doesn’t look too hard, right?—you’d see a blob of churning, complex mist in configuration space, with little blobs racing around and splitting into smaller blobs as waves propagated.

If you tried to calculate the quantum state of a single hydrogen atom over time, apart from the rest of the universe—which you can only really do if the hydrogen atom isn’t entangled with anything—the atom’s quantum state would evolve over time; the mist would churn.

But suppose you think about the whole universe at once, including yourself, of course. Because—even in the standard model of quantum physics!—that is exactly the arena in which quantum physics takes place: A wavefunction over all the particles, everywhere.

If you can sensibly talk about the quantum state of some particular hydrogen atom, it’s only because the wavefunction happens to neatly factor into (hydrogen atom) * (rest of world).

Even if the hydrogen atom is behaving in a very regular way, the joint wavefunction for (hydrogen atom * rest of world) may not be so regular. Stars move into new positions, people are born and people die, digital watches tick, and the cosmos expands: The universe is non-recurrent.

Think of how the universal wavefunction ψ(r, t) might behave when r is the position of all the particles in the universe.

Let’s call 9:00am the time t=0, measured in seconds.

At ψ(r, t=0), then, you are wondering what time it is: The particles making up the neurons in your brain, are in positions r_you that correspond to neurons firing in the thought-pattern “What time is it?” And the Earth, and the Sun, and the rest of the universe, have their own particles in the appropriate r_{rest-of-universe}. Where the complete r roughly factorizes as the product (r_you * r_{rest-of-universe}).

Over the next second, the joint wavefunction of the entire universe evolves into ψ(r, t=1). All the stars in the sky have moved a little bit onward, in whatever direction they’re heading; the Sun has burned up a little more of its hydrogen; on Earth, an average of 1.8 people have died; and you’ve just glanced down at your watch.

At ψ(r, t=2), the stars have moved a little onward, the galaxies have rotated, the cosmos has expanded a little more (and its expansion has accelerated a little more), your watch has evolved into the state of showing 9:00:02 AM on its screen, and your own mind has evolved into the state of thinking the thought, “Huh, I guess it’s nine o’ clock.”

Ready for the next big simplification in physics?

Here it is:

We don’t need the t.

It’s redundant.

The r never repeats itself. The universe is expanding, and in every instant, it gets a little bigger. We don’t need a separate t to keep things straight. When you’re looking at the whole universe, a unique function ψ of (r, t) is pretty much a unique function of r.

And the only way we know in the first place “what time it is”, is by looking at clocks. And whether the clock is a wristwatch, or the expansion of the universe, or your own memories, that clock is encoded in the position of particles—in the r. We have never seen a t variable apart from the r.

We can recast the quantum wave equations, specifying the time evolution of ψ(r, t), as specifying relations within a wavefunction ψ(r).

Occam’s Razor: Our equations don’t need a t in them, so we can banish the t and make our ontology that much simpler.

An unchanging quantum mist hangs over the configuration space, not churning, not flowing.

But the mist has internal structure, internal relations; and these contain time implicitly.

The dynamics of physics—falling apples and rotating galaxies—is now embodied within the unchanging mist in the unchanging configuration space.

This landscape is not frozen like a cryonics patient suspended in liquid nitrogen. It is not motionless as an isolated system while the rest of the universe goes on without it.

The landscape is timeless; time exists only within it. To talk about time, you have to talk about relations inside the configuration space.

Asking “What happened before the Big Bang?” is revealed as a wrong question. There is no “before”; a “before” would be outside the configuration space. There was never a pre-existing emptiness into which our universe exploded. There is just this timeless mathematical object, time existing within it; and the object has a natural boundary at the Big Bang. You cannot ask “When did this mathematical object come into existence?” because there is no t outside it.

So that is Julian Barbour’s proposal for the next great simplification project in physics.

(And yes, you can not only fit General Relativity into this paradigm, it actually comes out looking even more elegant than before. For which point I refer you to Julian Barbour’s papers.)

Tomorrow, I’ll go into some of my own thoughts and reactions to this proposal.

But one point seems worth noting immediately: I have spoken before on the apparently perfect universality of physical laws, that apply everywhere and everywhen. We have just raised this perfection to an even higher pitch: everything that exists is either perfectly global or perfectly local. There are points in configuration space that affect only their immediate neighbors in space and time; governed by universal laws of physics. Perfectly local, perfectly global. If the meaning and sheer beauty of this statement is not immediately obvious, I’ll go into it tomorrow.

And a final intuition-pump, in case you haven’t yet gotten timelessness on a gut level...

Think of this as a diagram of the many worlds of quantum physics. The branch points could be, say, your observation of a particle that seems to go either “left” or “right”.

Looking back from the vantage point of the gold head, you only remember having been the two green heads.

So you seem to remember Time proceeding along a single line. You remember that the particle first went left, and then went right. You ask, “Which way will the particle go this time?”

You only remember one of the two outcomes that occurred on each occasion. So you ask, “When I make my next observation, which of the two possible worlds will I end up in?”

Remembering only a single line as your past, you try to extend that line into the future -

But both branches, both future versions of you, just exist. There is no fact of the matter as to “which branch you go down”. Different versions of you experience both branches.

So that is many-worlds.

And to incorporate Barbour, we simply say that all of these heads, all these Nows, just exist. They do not appear and then vanish; they just are. From a global perspective, there is no answer to the question, “What time is it?” There are just different experiences at different Nows.

From any given vantage point, you look back, and remember other times—so that the question, “Why is it this time right now, rather than some other time?” seems to make sense. But there is no answer.

When I came to this understanding, I forgot the meaning that Time had once held for me.

Time has dissolved for me, has been reduced to something simpler that is not itself timeful.

I can no longer conceive that there might really be a universal time, which is somehow “moving” from the past to the future. This now seems like nonsense.

Something like Barbour’s timeless physics has to be true, or I’m in trouble: I have forgotten how to imagine a universe that has “real genuine time” in it.

Part of The Quantum Physics Sequence

Next post: “Timeless Beauty”

Previous post: “Relative Configuration Space”

[Hopefully_Anonymous]

it’s an interesting theory.

[mcandre]

I have one exception to the description of timeless physics: Each node in the tree represents a different state than its parent node. This is a time step. A time step that is not instantaneous—we still observe the universe unfolding. Have you looked into cellular automata? This is how I view the universe.

http://​​en.wikipedia.org/​​wiki/​​Cellular_automata

P.S. I’m reading Harry Potter and the Methods of Rationality and absolutely loving it! Have you read Crimes Against Logic?

http://​​www.amazon.com/​​dp/​​0071446435/​​

[Jadagul]

Interestingly (at least, I think it’s interesting), I’d always felt that way about time, before I learned about quantum mechanics. That’s what a four-dimensional spacetime means, isn’t it? And so science fiction stories that involve, say, changing the past have never made any sense to me. You can’t change the past; it is. And no one can come from the future to change now, because the future is as well. Although now that I think about it more, I realize how this makes slightly more sense in this version of many-worlds than it does in a collapse theory.

[FeepingCreature]

Belatedest answer ever: don’t think of it as changing the past, think of it as establishing a causal link to an alternate version of the past that had you appear in a time machine (and obeys other constraints, depending on the time travel rules of the story).

[chaosmosis]

It’s nice to know that someone else thought of this stuff as well. Here’s what led me to the same conclusion without reading any hard science.

I got really obsessed with Zeno’s paradox a few months ago and managed to figure all of this out independently, using similar arguments to come to the same conclusion. Time is just change over space. There are lots of parallels between what the arguments made here and what Zeno said. It’s not identical, but thinking of Zeno led me to tangents that led me to think of this article.

I also read some quote by Einstein in a letter to a friend after the death of a loved one, saying that the death/​life distinction is weird because there are space configurations in which people who have already died still exist. That helped too.

Some of the stuff on this site also influenced my thought process: www.scottaaaronson.com/​​writings/​​ (Pancake is the best one.)

And lastly there’s a thought experiment meant to “prove” that time exists independently of change which failed miserably once I thought about it so it influenced me to move in the opposite direction.

You have three universes, galaxies, planets, rooms, whatever, labelled A B and C. All motion in room A is set to stop every two years and once it’s stopped it stays stopped for a year. All motion in room B is set to stop every three years and once it’s stopped it stays stopped for a year. All motion in room C is set to stop every six years and once it’s stopped it stays stopped for a year. Then, supposedly, when they all finish the sixth year and move on to the seventh year they would all “wake up” at the same time and be able to tell that time passed because their cycles relative to each other would have stopped.

My response was to say that it seemed like all time everywhere would stop if they all coincided (assuming that A B and C contained everything in all the universes), but also that the premises were flawed (assuming that A B and C did not contain everything) because a change in their cycles relative to each other was impossible without time existing in the interim. Their cycles cannot change relative to each other if one wishes to try to prove that time exists without change, the problem cheats by sneaking in a change disguised as the lack of change. The ultimate flaw in the problem which those problems stem from is presuming a larger existence outside of room A B and C in which the problem poser is posited and able to watch their relative cycles shift. I can’t conceive of any way that would happen.

Lastly I thought that insofar as time might exist external to change it seems like an absolutely meaningless concept anyway. I don’t care about “time”, I care about material conditions and structures and the formations of certain things relative to me.

[VAuroch]

You have an extra a in aaaronson.

[steven]

And yes, you can not only fit General Relativity into this paradigm, it actually comes out looking even more elegant than before.

Eliezer, do you realize the difference between Barbour’s treatments of classical mechanics and GR? In GR, he bases everything not just on relations between matter, but on relations between matter and space itself (at least its metric structure). When he calls his theory “relational” he is engaging in wordplay. The Pooley paper I linked in yesterday’s comments goes into gory philosophical detail on this.

I think some people (not including Eliezer) see that Barbour says “there is no time” and imagine that he invented the idea of a block universe (which I personally don’t see any philosophical problems with). But it’s everyone else who believes in block universes; Barbour’s universe is an unsorted-pile-of-block-slices universe. Barbour’s theory de-unifies space and time. Ouch!

Lee Smolin is one of the people behind relational QM, and he’s a naive Popperian. To me he’s the closest thing that physics has to a philosophical anti-authority.

[steven]

Asking “What happened before the Big Bang?” is revealed as a wrong question. There is no “before”; a “before” would be outside the configuration space. There was never a pre-existing emptiness into which our universe exploded. There is just this timeless mathematical object, time existing within it; and the object has a natural boundary at the Big Bang. You cannot ask “When did this mathematical object come into existence?” because there is no t outside it.

This has been true of the standard (FRW) big bang models since, what, the 1920s?

[Deleet]

It’s called a loaded question. http://​​www.fallacyfiles.org/​​loadques.html

I invented a logic that can deal with questions and answers. It allows one to formalize questions with an adequately expanded predicate logic. Here’s a formalization of the question:

(∃x)(∃t1)(∃t2)(BBHappenedAt[t1]∧HappenedAt[x,t2]∧Before[t2,t1])∧(x=?)

English: There is a thing, x, there are two points of time, t1 and t2, big bang happened at time t1, and x happened at time t2, and t2 is before t1, and what is x?

But if the empirical claim holds, which it does AFAIK, that BB was the first event, i.e. no prior events, then the question is false. Whatever has a false implication is itself false, or whatever is inconsistent with a truth is false.

I know a lot of physics students and some of them teach high school physics for money, and I asked them how they deal with the question. One of them said that he just gives them an analogy, it goes like this:

What is north of the north pole?

Formalized:

(∃x)(IsNorthOf[x,n])∧(x=?)

n = north pole

EN: There is a location such that it is north of the north pole, and what is it?

but we know that there is nothing north of the north pole. Because per definition it is the northernmost spot, i.e.:

(∃x)¬(∃y)(IsNorthOf[y,x]∧x=n)

EN: There is a location, x, and there isn’t a location, y, such that y is north of x, and x is identical to the north pole. That is the definition formally speaking.

The question then is similarly false, because it has a false implication, or equivalently, is inconsistent with a truth (in this case a necessary truth, not a contingent).

Hope this helps with similar questions, e.g. “Why is there something rather than nothing?” (implying there is a reason/​explanation, which I see no reason to accept).

[Luke_A_Somers]

I wouldn’t go so far as to say you invented it, but reinvented seems appropriate.

[Deleet]

Can you point to someone else who invented it before me? ‘Reinvented’ implies ‘invented’ in any case.

[Shmi]

Nothing as formal as a notation, but a standard reply of an expert to a novice’s question “What happened before the Big Bang?” is “Why do you assume that there must [always] be a “before”?” is basically the same thing.

[Deleet]

Yes, but it is not a formal system, and it’s a wonder no one else (afaik) did a formal system for questions and answers.

[Luke_A_Somers]

It seems like it’s… hmm. I guess this is different from what I thought it was originally.

[TonyB]

Asking the question “What happened before the Big Bang” is legitimate in the context that it is questioning the assumption of a Big Bang to begin with. If we say there is nothing outside the configuration space we have just proclaimed there is something called space; meaning there is an object with a boundary. We cannot have a boundary without something outside that boundary since that what defines the boundary to begin with. If we say there is no boundary to space then there is no expansion of space to begin with since it has no boundary and has always been spatially infinite. If we say there is a timeless mathematical object with time existing within it then we have just contradicted ourselves by saying it has no time yet it has it itself. By calling it a timeless mathematical object we are saying it doesn’t exist except in our concept of it and since we are conceiving of it now it does exist since how could it not if we are able to conceive of it, and that conception has not changed over billions of years and since no change equals no time it is eternal. And if there is no t outside of it then there can be not expansion of it since it has no boundary, hence any notion of the Big Bang being an expansion of time and space remains such as that, a notion—without real physical reality; There was no beginning of say 14 billion, 18 billion years ago...it has always been and always will be.

[Frustrated]

Ah. And suppose I snapped my fingers and caused all the stars and galaxies to move into the appropriate positions for 2108?

“You’d be arrested for violating the laws of physics.”

But suppose I did it anyway.

I get so frustrated when you write stuff like this because you also wrote: http://​​lesswrong.com/​​lw/​​if/​​your_strength_as_a_rationalist/​​

Therefore at this point my answer is no you did not.

However, funnily enough, once you changed all the atoms in the universe my response was “Okay now it is 2108” (maybe because I found the universe in a consistent believable state including my memories of the intevening 100 years).

And by the way since I would have survived for another 100 years I might just have overwhelming personal evidence that Many Worlds is true. I guess that would be your purpose for the exercise. (Of course if you are still there with me after that 100 years then the overwhelming personal evidence doesn’t happen).

I have been learning a lot from your quantum mechanics series. Thanks. Please keep it up.

[JessRiedel]

You’ve drawn many vague conclusions (read: words, not equations or experimental predictions) about the nature of reality from a vague idea promoted by a non-academic. It smacks strongly of pseudo-science.

Julian Barbour’s work is unconventional. Many of his papers border on philosophy and most are not published in prominent journals. His first idea, that time is simply another coordinate parameterizing a mathematical object (like a manifold in GR) and that it’s specialness is an illusion, is ancient. His second idea, that any theory more fundamental than QM or GR will necessarily feature time only in a relational sense (in contrast to the commonly accepted, and beautiful, gauge freedom of all time and space coordinates) is interesting and possibly true, but it is most likely not profound. I can’t read all of his papers, so perhaps he has some worthwhile work.

This post, however, appears to be completely without substance. What is the point?

• That the universe as we understand it is best described by a timeless mathematical object (e.g. a manifold equipped with some quantum fields)? This viewpoint, taken by most physicists, has been around since at least the 1920′s. While profound, it has little to do with Barbour’s work, which seems to be the focus of this post.

That the next theory of physics should be expressed with a “relational approach”? This is a nice idea, but one which has (to my knowledge) produced no objective progress in formulating a successor to GR or QM. There are a thousand approaches out there with similar promise...and similar results. I can’t help but feel that you are wading into waters which are above your expertise.

[Luke_A_Somers]

will necessarily feature time only in a relational sense (in contrast to the commonly accepted, and beautiful, gauge freedom of all time and space coordinates)

I find this contrast you’re drawing confusing. Making it relational is an attempt to justify the gauge freedom.

[Arthur]

“We don’t need the t.

It’s redundant.

The r never repeats itself.”

While this seems to be true given the expansion of the universe, is it strictly necessary? What if some value R does repeat, throwing the universe into an endless loop? At some point, the chains of r’s leading up to R0 and R1 would differ; wouldn’t we need another variable to encode that?

[Dojan]

...throwing the universe into an endless loop? At some point, the chains of r’s leading up to R0 and R1 would differ...

The point of an endless loop is that it is endless and R never will differ outside of that loop, how could it? Everything happens exactly the same way it did last time, and for exactly the same reasons. A universe also can’t enter such a loop starting outside (given reversible physics), and there wouldn’t be any seem where it is all stiched together.

I’m not sure how this would go together with many-worlds. But if one considers two branches, where one branch eventually gets into exactly the same configuration at some point of the other (extremely unlikely, obviously, but consider all possible branches...), we could compress our model of reality without loosing information by treating them as one. This is quite similar to the endless loop above.

(I am not a phycisist!)

[Eisenherz]

Then, it would render the configuration a Periodic function, yet Periodic functions are still parameterized by a time-factor.

[imaxwell]

Well sure, if you parametrize with a time factor the result will be a periodic function. But you can still de-parametrize and simply have a closed loop described relationally. A parametrization of a circle usually consists of periodic functions, but that doesn’t mean the circle itself is periodic. It’s just there.

Also remember that “exactly the same configuration” means exactly the same configuration, of everything, including for instance your calendar, your watch, and your brain and its stored memories. So pretty much by definition there would be no record of such a thing happening. We wouldn’t need another variable to encode it because we wouldn’t need to encode it in the first place.

[Caledonian2]

I can’t help but feel that you are wading into waters which are above your expertise.

Wading?

Eliezer is not beckoning, but drowning.

But your argument is flawed. Discarding an argument because you don’t feel it’s ‘profound’ is an error. There are scores of mundane truths that go ignored because they’re not ‘profound’ enough to interest the self-styled philosophers, and countless empty ‘profundities’ that mean nothing.

Most of the ‘eternal questions’ have already been answered. The trick is to recognize this and move on.

[g]

Interesting aesthetic question raised by Caledonian’s comment: “not beckoning, but drowning” versus “not wading, but drowning”. I think the latter would have worked much better, but presumably C. thought it too obvious and wanted to preserve more of Stevie Smith’s semantics. :-)

Arthur, what would keeping a time coordinate buy you in your scenario? Suppose, simplifying for convenience, we have A → B → C → B [cycle], and suppose each state completely determines its successor. What advantage would there be to labelling our states (A,0), (B,1), (C,2), (B,3), (C,4), etc., instead of just A,B,C? Note that there’s no observable difference between, say, (B,1) and (B,3); in particular, no memory or record of the past can distinguish them because those things would have to be part of state B itself.

I think David Deutsch has a similar unsorted-pile-of-block-slices view of the world. I don’t know if either was influenced by the other.

[Shane_Legg]

Stop it!

If I intuitively took on board your timeless MWI view of the world… well, I’m worried that this might endanger my illusion of consciousness.

Thinking about it is already making me feel a bit weird.

[JulianMorrison]

Whence comes the experience of a present moment?

[Arthur]

g, I’m not sure how it all works out in terms of ψ, as the mathematics of multi-dimensional configuration spaces is way over my head. What I’m not clear on is, in the absence of t, why do we have to read the function from “left to right?” When you read in the other direction, State C can “lead to” A or B. Don’t we need a variable to differentiate between the C that leads to A, and the C that leads to B, to as Eliezer put it, “keep things straight”?

[Arthur]

Oops, I meant State B can lead to A or C.

[ME3]

Doesn’t the Lorentz invariant already pretty much take care of the relativity of time? As long as we’re using the Lorentz invariant, we’re free to reparameterize the universe any way we want, and our description will be the same. So I don’t see what this Barbour guy is going on about, it seems like standard physics. Whether you write your function f(x,t) or f(y) where y = g(x,t) or even just f(x) where t = h(x) is totally irrelevant to the universe. It’s just another coordinate transformation just like translating the whole universe by ten meters to the left.

Now, if you have a new invariant to propose, THAT would amount to an actual change in the laws of physics.

[Günther_Greindl]

@Jess

Your comments on Barbour (non-academic etc) are ad hominem, I say so what? Being an academic may be an indicator for good work, but not more. And he did his Ph.D in physics anyway.

Julian Barbour’s work is unconventional.

Yes! Fine. Lovely. Science needs more unconventional thinkers. Let the evidence sort them out, but let’s not be against “unconventional” theories. Especially not when they are explanatorily powerful.

Many of his papers border on philosophy

There are two kinds of philosophy: the bad kind (Essay by Paul Graham criticising philosophy , “How to do philosophy”; Paul featured just recently on OC).

And the good kind: the kind Albert Einstein was actually performing when he examined the laws of physics and derived his GRT from general (philosophical?) considerations. His ideas were definitely unconventional at the time.

@Eli Thanks for your Barbour series, I read Barbour about a year ago but had already before come to the conviction that the flow of time must be an illusion. In the end, a theory of everything must forego an “outside” time dimension. There can be no “supertime” (that’s what I call it ;-) ) above or outside the universe/​multiverse, apart from relative configurations.

And if you would look at the whole universe from the outside (which is of course per definition impossible) the timeless and fundamentally static nature of everything would reveal itself quite simply (I’m getting carried away).

I hope many physicists read your post, as the Barbour theory deserves grad students working on the details—it is, I am deeply convinced, the right direction to pursue, difficulties in the formalism notwithstanding.

Time is, contrary to widespread belief, no mystery.

[Caledonian2]

Whence comes the experience of a present moment?

The after-the-fact processing done by the brain of the data accumulated in that moment, of course.

If that storage is disrupted—by sudden trama or an experiential shock, such as that which might occur in a car accident without leaving lasting damage—there are no experiences at all.

If there are no lasting consequences of an event that our physiology can react to, it’s as though it never happened at all, at least as far as our awareness is concerned. If you have no high-level memory representation of an event, and no low-level physiological response resulting from it, as far as you’re concerned it didn’t happen.

Understanding this is key to recognizing how coherent perceptions arise from the utter chaos of the Library.

[TonyB]

″ - there are no experiences at all. ”

Except the experience of no experience...experiencing being aware of being aware which requires no sensory input or even a physical body with a brain, that is when the true present moment occurs since it has always been and always will be...there is no time with awareness being aware that it is aware.

[JulianMorrison]

Caledonian, you miss the point. The present moment seems distinguishable from the past or future, singular, and in constant motion. Experience exists in the present and describes the past via memory and the future via speculation. The content of experience changes.

Even if this is a cognitive illusion, it needs a reason.

[ME3]

But the main thing that’s different about time is that it has a clear direction whereas the space dimensions don’t. This is caused by the fact that the universe started out in a very low-entropy state, and since then has been evolving into higher entropy. I don’t know if it’s even possible to answer the question of why the universe started out the way it did—it’s almost like asking why anything exists at all. But whatever the reason, the universe is very uniform in its space dimensions, but very non-uniform in its time dimension.

[poke]

In philosophy “four dimensionalism” is probably the dominant view of time. We’re all spacetime worms in a block universe. I don’t know what to make of some of Barbour’s ideas but I can swallow timelessness.

It’s worth noting, regarding Jadagul’s comment, that time travel should be possible in a block universe without paradox and without resorting to many-worlds. The closed time-like curve just exists as part of the block universe and the illusion of paradox stems from our foreknowledge of events. It’s not required that we be able to change things (since there’s no free will in a block universe) but the fact that we know that we’ll be unsuccessful in our attempts to change things is merely strange and not paradoxical. David Lewis has a good discussion of this in his paper The Paradoxes of Time Travel.

[Caledonian2]

The present moment seems distinguishable from the past or future, singular, and in constant motion.

The ‘present’ is always the immediate past. We’re not aware of things happening in the true present, because our nervous system doesn’t have anything to process. It can only receive data corresponding to the very recent past, and then it takes even more time to process it.

The reality is that our awareness operates on a measureable time-lag.

[Manon_de_Gaillande]

For some reason, this view of time fell nicely in place in my mind (not “Aha! So that’s how it is?” but “Yes, that’s how it is.”), so if it’s wrong, we’re a lot of people to be mistaken in the same way.

But that doesn’t dissolve the “What happened before the Big Bang?” question. I point at our world and ask “Where does this configuration come from?”, you point at the Big Bang, I ask the same question, and you say “Wrong question.”. Huh?

[imaxwell]

Super-late answer!

If you ask about a configuration X, “Where does this configuration come from?” I will point at a configuration W for which the flow from W to X is very high. If you ask, “Well, where does W come from?” I will point to a configuration V for which the flow from V to W is very high. We can play this game for a long time, but at each iteration I will almost certainly be pointing to a lower-entropy configuration than the last. Finally I may point to A, the one-point configuration. If you ask, “Where does A come from?” I have to say, “There is nowhere it comes from with any significant probability.” At best I can give you a uniform distribution over all configurations with epsilon entropy. But all this means is that no configuration has A in its likely future.

The thing is, it doesn’t make sense to ask what is the probability of a configuration like A, external to the universe itself: you can only ask the probability that a sufficiently long path passing through some specific configuration or set of configurations will have A in

• its future, or

• its past. The probability of the former is probably 0, so we don’t expect a singularity in the future. That of the latter is probably 1, so we do expect a singularity in the past.

[Stirling_Westrup]

The thing about the concept of a block universe that bothers me is the question of the reversibility of the Schrödinger equations. I have been told that they are so, but I have to take it on faith that they are completely time-symmetric since they are just beyond where I am comfortable in Mathematics.

So, if one looks at the current configuration space for a point of ‘now’, and works the equations backwards, does one get only one possible past, or an large number of possible pasts? If its the former, how can one claim that the equations are time symmetric? If its the latter, why don’t we remember all of those quantum possibilities?

[Caledonian2]

I point at our world and ask “Where does this configuration come from?”

There is no phenomenon within time that can be used as an explanation for the configuration, as is required by the phrase “come from”. Furthermore, if we try to explain a thing by referring to another thing, we then need an explanation for the other thing.

There is no reason for the configuration of time within time, and even if we adopt a timeless perspective, we can never find an ultimate resolution to the question. The universe simply is what it is. Your question is surely asked in good faith, but it’s not meaningful.

[JessRiedel]

Günther: Of course my comments about Barbour were (partially) ad hominem. The point was not to criticize his work, but to criticize this post. Very few people are qualified to assess the merit of Barbour’s work. This includes, with respect, Eliezer. In the absence of expertise, the rational thinker must defer to the experts. The experts have found nothing of note in Barbour’s work.

Albert Einstein was not performing philosophy when he developed GR. He was motivated by a philosophical insight and then did physics.

[Eliezer Yudkowsky]

I wasn’t intending to suggest that the timelessness of the universe is an answer to the First Cause puzzle (which itself is certainly a Wrong Question, somehow) because you just point to the whole timeless mathematical object and say, “Why does this ‘exist’?”

It’s just that you can’t answer by tracing to one minute before the Big Bang and some mighty act of the Flying Spaghetti Monster. You’ll have to look somewhere else for a resolution to your confusion.

@Stirling: If you took one world and extrapolated backward, you’d get many pasts. If you take the many worlds and extrapolate backward, all but one of the resulting pasts will cancel out! Quantum mechanics is time-symmetric.

@Shane Legg: Good to see that the post had its intended effect.

[xelxebar]

“If you took one world and extrapolated backward, you’d get many pasts. If you take the many worlds and extrapolate backward, all but one of the resulting pasts will cancel out! Quantum mechanics is time-symmetric.”

My immediate thought when reading the above: when extrapolating forward do we get cancelation as well? Born probabilities?

[wizzwizz4]

We do get some, e.g. inside a quantum computer, impossible worldstates cancel. But nowhere near as much.

[Furcas]

I wasn’t intending to suggest that the timelessness of the universe is an answer to the First Cause puzzle (which itself is certainly a Wrong Question, somehow) because you just point to the whole timeless mathematical object and say, “Why does this ‘exist’?”

“What caused the universe?” and “Why does this universe exist, rather than any other possible universe?” are two completely different questions. I think the first one is answered satisfactorily by the timelessness of the universe as a whole. The second might be answered by something like Tegmark’s level IV multiverse.

[Constant2]

So, if one looks at the current configuration space for a point of ‘now’, and works the equations backwards, does one get only one possible past, or an large number of possible pasts? If its the former, how can one claim that the equations are time symmetric? If its the latter, why don’t we remember all of those quantum possibilities?

Both. Many possible pasts, because the many worlds are never entirely causally isolated, so we are to some minuscule degree always affected by parallel worlds (though not enough to notice). But one possible past, because only one of these has any great influence on us (or so it seems for the most part—exceptions aside, e.g. mangled worlds aside). If you want to know how it is possible to have symmetric equations but at the same time the asymmetry of division of worlds in one direction in time, the standard explanation is thermodynamic. It’s fundamentally the same reason that if you drop a glass it breaks but if you drop the shards of glass they don’t spontaneously mend themselves.

[Dynamically_Linked]

This abstract of one of Barbour’s papers may be helpful for those wondering (like me) how exactly Barbour was proposing to get rid of “t”:

http://​​www.iop.org/​​EJ/​​abstract/​​0264-9381/​​11/​​12/​​006

Abstract. A strategy for quantization of general relativity is considered in the context of the timelessness' of classical general relativity discussed in the preceding companion paper. The Wheeler--DeWitt equation (WDE) of canonical quantum gravity is interpreted as being like a time-independent Schrödinger equation for one fixed energy, the solution of which simply gives, once and for all, relative probabilities for each possible static relative configuration of the complete universe. Each such configuration is identified with a possible instant of experienced time. These instants are not embedded in any kind of external or internal time and, if experienced, exist in their own right. The central question is then: Whence comes the appearance of the passage of time, dynamics, and history? The answer proposed here is that these must all becoded’, in the form of what appear to be mutually consistent `records’, in the individual static configurations of the universe that are actually experienced. Such configurations are called time capsules and suggest a new, many-instants, interpretation of quantum mechanics. Mott’s explanation of why -particles make straight tracks in Wilson cloud chambers shows that the time-independent Schrödinger equation can concentrate its solution on time capsules. This demonstrates how the appearance of dynamics and history can arise in a static situation. If it can be shown that solutions of the Wheeler—DeWitt equation are spontaneously and generically concentrated on time capsules, this opens up the possibility of an explanation of time at a very deep level: the timeless wavefunction of the universe concentrates the quantum mechanical probability on static configurations that are time capsules, so that the situations which have the highest probability of being experienced carry within them the appearance of time and history. It is suggested that the inescapable asymmetry of the configuration space of the universe could play an important role in bringing about such concentration on time capsules and be the ultimate origin of the arrow of time.

[Constant2]

If you took one world and extrapolated backward, you’d get many pasts. If you take the many worlds and extrapolate backward, all but one of the resulting pasts will cancel out!

I agree. However, at the same time, we don’t actually remember the many extrapolated pasts of the one world we inhabit. Of course, “remembering” multiple extrapolated pasts might be indistinguishable from failing to remember any particular past (e.g., if both X and not-X lie in our extrapolated past, then our “remembering” both X and not-X might be nothing other than failing to remember whether X or not-X).

[Psy-Kosh]

Well, I’m not sure there’s no observable difference. I mean, let’s say you have universe in state |A> such that the evolution of the state vector would cause it one nanosecond later (whatever the heck that turns out to really mean) to be, oh, say something like (-|A> + |B>)/​sqrt(2)

Now, if time was truly nonexistant then those two would interfere with each other, right? ie, it’s sortakinda the same sort of test to find out if two particles are really identical or not.

Except, wait, if we’re talking total state of reality… how would one perform the experiment in the first place? what “clock” would one use? Okay, I think I’m starting to see it. So what’s analogous to time? something like the euclidian distance between two configurations? |(r2 - r1)| or something like that? Actually, if so, then that would also pretty much make it clear that you can slice configuration space anyway you want to obtain surfaces of simultaneaty… Okay, I think I’m starting to like this idea better now.

[anonymous31]

Is the possibility of life in non conventional coordinates occurring been discarded?

By this i mean evolution were selection is made along some coordinate of space, or backwards in time.

Maybe it would make a good Sci-Fi finding some intelligent life form which evolved from the future to the past, meeting humanity at present.

[Recovering_irrationalist]

@anonymous

[steven]

Eliezer and DL, here’s a philosophy paper discussing parity in relational physics.

[Nick_Tarleton]

I agree with those who can’t quite see the point of this post (block universe is old and uncontroversial), but I suppose that may because I internalized (mostly) this view some time ago. I see some people are learning from it.

Something like Barbour’s timeless physics has to be true, or I’m in trouble: I have forgotten how to imagine a universe that has “real genuine time” in it.

I hope you’re not saying this is a good thing, or that others should follow.

[poke]

I’m a huge fan of the general program of philosophical minimalism (i.e., doing away with epiphenomena). One of my favorite works in this respect is Hartry Field’s Science Without Numbers. There’s a long line of argument in philosophy for the reality of mathematical abstracta on the grounds of its indispensability to science. Field formulated a version of classical physics without numbers.

[Dynamically_Linked]

Barbour is proposing something quite different from the block universe. I’m not sure if Eliezer is missing the point, or just not carrying it across. Barbour is speculating that if we solve the Wheeler-DeWitt equation, we’ll get a single probability distribution over the configuration space of the universe, and all of our experiences can be explained using this distribution alone. Specifically, we don’t need a probability distribution for each instant of time, like in standard QM.

I think Eliezer’s picture with the happy faces is rather misleading, if it’s suppose to represent Barbour’s idea. I’d fix it by getting rid of the arrows, jumble the faces all around so that there is no intrinsic time-like ordering between them, and then attach a probability to each face that together add up to less than 1.

Steve, thanks for the paper link. Parity violation clearly represents a big problem to relational physics, and I’m glad I’m not the only one who noticed. :)

[Doug_S.]

It’s worse than just P-symmetry (parity) violation. There’s also CP-symmetry (charge-parity) breaking, which, given CPT symmetry (a fairly reasonable assumption given current knowledge) means that the weak nuclear force also violates T-symmetry. Even without the second law of thermodynamics, you would be able to put an arrow to time by observing the decay of certain particles.

Therefore, we need time.

[peco]

Does a universe consisting of a single particle change?

[Dynamically_Linked]

I went back to the beginning of this series of posts, and found this introduction:

I think I must now temporarily digress from the sequence on zombies (which was a digression from the discussion of reductionism, which was a digression from the Mind Projection Fallacy) in order to discuss quantum mechanics. The reasons why this belongs in the middle of a discussion on zombies in the middle of a discussion of reductionism in the middle of a discussion of the Mind Projection Fallacy, will become apparent eventually.

Eliezer, would you mind telling us the reasons now, instead of having them become apparent eventually? I ask this because I’d like to know, if I detect some error or confusion in the posts or comments, whether it’s central to your eventual point, or if it’s just an inconsequential nit. Do you actually need Barbour’s timeless physics to make your point, or would the standard block universe do? I’d like to skip explaining the difference between the two if the difference doesn’t really matter. I mean we’re not here to learn about some speculative physics for its own sake...

[Z._M._Davis]

“I mean we’re not here to learn about some speculative physics for its own sake...”

We’re not? Did I miss a memo?

[Craig_Morgan2]

@Nick Tarleton, anyone questioning the value of this post Prior to this post, my understanding was that there wasn’t one ‘me’ consciously observing the unraveling of our universe over time. Instead, there were many of ‘me’, each observing a different universe, and with every irreversible thermodynamic event, more universes and instances of ‘me’ were being created.

This post blew my mind.

@Julian “Whence comes the present moment?” Now I understand that “I” am not a consciousness traveling through time. Instead, my consciousness is represented in a sub-space of the immensely-dimensional configuration space. Time is an illusion. Everywhere that my consciousness is represented within the many-world many-moment configuration space; it will feel like it is traveling through ‘time’. “I” feel like I am traveling through time because “I” am a structure that models both itself and the evolution of sensory data. At every point that “I” am represented in the configuration-state, “I” IS this model of itself and the ‘previous’ states of the world, thereby fooling “I” into modeling and experiencing ‘time’.

@Everyone Manon de Gaillande asked “Where does this configuration come from?” Seeing no answer yet, I’m also intrigued by this. Does it even make sense to ask it? If it doesn’t, please help Manon and I dissolve the question.

[jiohdi]

@Craig_Morgan2 At every point that “I” am represented in the configuration-state, “I” IS this model of itself and the ‘previous’ states of the world, thereby fooling “I” into modeling and experiencing ‘time’.

everything you are writing implies motion which does not exist in a blockhead universe. sorry, but a static being by any rational definition is a dead being incapable of experiencing anything at all. there is no past nor present nor even anticipation of a future without motion and you cannot have motion in a static universe unless you believe you exist outside it.

[iwdw]

Manon de Gaillande asked “Where does this configuration come from?” Seeing no answer yet, I’m also intrigued by this. Does it even make sense to ask it? If it doesn’t, please help Manon and I dissolve the question.

It doesn’t make sense in the strict sense, in that barring the sudden arrival of sufficiently compelling evidence, you aren’t going to be able to answer it with anything but metaphysical speculation. You aren’t going to come out less confused about anything on the other side of contemplating the question.

Furthermore, no answer changes any of our expectations—whether or not we’re a naturally occurring phenomenon or a higher-dimensional grad student’s Comp Sci thesis has no effect on any of our experiences within this universe.

[Nick_Tarleton]

Furthermore, no answer changes any of our expectations—whether or not we’re a naturally occurring phenomenon or a higher-dimensional grad student’s Comp Sci thesis has no effect on any of our experiences within this universe.

You’re not imaginative enough. If the latter is true, we’re a lot more likely to see messages from outside the Matrix sometime. (“Sorry, guys, I ran out of supercomputer time.”)

[iwdw]

You’re not imaginative enough. If the latter is true, we’re a lot more likely to see messages from outside the Matrix sometime. (“Sorry, guys, I ran out of supercomputer time.”)

For various values of “a lot”, I suppose. If something is simulating something the size of the universe, chances are it’s not even going to notice us (unless we turn everything into paper clips, I suppose). Just because the universe could be a simulation doesn’t mean that we’re the point of the simulation.

[Stirling_Westrup]

@Eliezer: You say If you took one world and extrapolated backward, you’d get many pasts. If you take the many worlds and extrapolate backward, all but one of the resulting pasts will cancel out!

If this is true, then why do we calculate forward based only on our current configuration? If we took all the many worlds in our possible pasts and extrapolated forward, would they cancel out all but a single future?

[Caledonian2]

If everything we know is but a simulation being run in a much larger world, then “everything we know” isn’t a universe.

If you can receive messages from outside of the Matrix, inside, the Matrix isn’t a universe either.

There is no outside to the universe. There’s isn’t anything there. There isn’t even nothing there. There isn’t even a there there. You’ve gone beyond the bounds of existence and nonexistence once you’ve left the universe behind.

[iwdw]

If everything we know is but a simulation being run in a much larger world, then “everything we know” isn’t a universe.

The question wasn’t “what’s outside the universe?”, it was “where did the configuration that we are a part of come from?”

I don’t think you can necessarily equate “configuration” (the mathematical entity that we are implicitly represented within), with “universe” (everything that exists).

[Tim_Tyler]

Viewing the universe as a timeless four-dimensional object—rather than the temporal evolution of a three-dimensional one—does not really buy you any “simplicity”—because then you need an additional explanation of why the four-dimensional object is structured in the way that it is.

[jiohdi]

you also need to explain motion which does not exist at all in a timeless 4d object. you need to explain how any static being can experience a present moment and moments leading up to it as past moments. and you need to explain how any perception is possible by a static being.

[Stephen_P._Schaefer]

I don’t understand “perfectly local or perfectly global”. My intuition of the Schroedinger equation is that it gives an approximation of the probability amplitude for a system, and that approximation is accurate to the extent that the system is isolated from the rest of the universe. The degree to which it is not accurate is the degree to which it is not isolated. An unentangled hydrogen atom in intergalactic space is fairly isolated; a hydrogen atom participating in an H2 molecule is not; but I argue that there are intermediate—“imperfect” states. And, given the big bang, no subsystem is going to be “perfectly” local because of its (once) proximity to other parts of the system. Nonetheless, our intergalactic hydrogen atom is going to behave indistinguishably close to the “perfectly” local model. Do you mean something else by “perfectly local or perfectly global”?

[Caledonian2]

“where did the configuration that we are a part of come from?”

That IS speculating about what is beyond the universe. Your question is unanswerable.

[amrit_sorli]

Dynamic Equilibrium of The Atemporal Universe

Amrit Srecko Sorli Scientific Research Centre BISTRA, Slovenia [e-mail]

In the book “Relativity: The Special and General Theory” (1920) Einstein discussed that it makes no sense to think about space-time as an independent physical quantity. The basic medium into which runs material change is gravitational field. Space-time is only a structural quality of a gravitational field: “Space-time does not claim existence on its own but only as a structural quality of the [gravitational] field” (1). The thesis here is that space-time as a structural quality of gravitational field is observer effect formed into the process of measurement. In quantum physics the term observer effect refers to changes that the act of observing will make on the phenomenon being observed; the observer is no longer external and neutral, but through the act of measurement he becomes himself a part of observed reality. Into scientific experiment “space-time” that is observer’s mathematical model also becomes structural quality of gravitational field. When there is no measurement, space-time exists only as a mathematical model and do not exist as a structural quality of gravitational field. Einstein and Gödel were right saying that there is no time in the universe, that universe is a timeless (atemporal) phenomenon (2). Time is what one measures with clocks. With clocks one measures duration and numerical order of material change that run into the gravitational field. Time enters into existence when one measures it (3,4). In the universe nothing is “before” or “later” irreversible stream of material change runs into gravitational field that is timeless (atemporal). Human’s experience this irreversible stream into concept of “space and time”, scientist’s into concept of “space-time”. Atemporal gravitational field is a “direct gravitational medium between massive objects”. Gravity force exists between basic elements of gravitational field called “quanta of gravity” that build up cosmic space. Gravity field has a different density that depends on the density of matter into given volume of gravity field. Higher is density of matter; lower is density of gravity field. In General Theory of Relativity gravitational force is result of curvature of space. Stellar objects change geometry of space. Bigger is mass of a stellar object, more space is curved, bigger is gravitational force. Here idea arises that curvature of space in General Theory of Relativity is a measure of quantum density of gravitational field. More space is curved, less is density of gravitational field . Less space is curved, higher is its density. Density of gravitational field increases with the distance from massive objects. Inside of massive objects density of field depends on density of mass . Higher is density of mass , lover is density of field . Where density of field is lower quanta of gravity are more “stretched” and have stronger tendency to “shrink”. This “shrinking” force is gravitational force that works between quanta of gravity. Gravity force keeps gravitational field together and that keeps together also three dimensional objects that exist into it. Atemporal gravitational field is a “direct gravity medium” between stellar objects. In a similar way atemporal gravitational field is a “direct information medium” between two elementary particles by “Einstein-Podolski-Rosen” experiment. Information does not travel between particle A and B, information is into gravitational field into which exist both of particles. Light is bend by passing massive stellar objects because of different density of gravity field through which moves. Physical space into which stellar objects exist cannot be curved on its own. Physical base of curvature of space is variable quantum density of gravitational field . Density of gravitational field inside of black holes, binary neutron stars, in the centre of galaxies Inside black holes density of gravity field is so low that gravity field has an enormous force of shrinking. This shrinking force disintegrates all subatomic particles back into quanta of gravity. Beyond Schwartschild radius mass transforms back into quanta of gravity. Black hole “sucks” matter from outer space and transforms it into quanta of gravity. Transformation “mass—quanta of space” continuously increases density of gravitational field in the centre of black hole that spreads with the light speed into outer space as a “gravitational waves”. Astronomical observations of diminishing of speed of rotation (orbit time) of binary neutron stars PSR1913+16 is explained by transformation of mass of stars into gravitational radiation. According to the understanding here gravitational radiation is result of transformation of mass of stars into quanta of gravity in the centre of binary stars (similar as in the centre of black holes). Transformation “mass—quanta of gravity” increases density of gravitational field in the centre of stars that spreads with the light speed into outer space as a “gravitational radiation”. Existence of gravitational waves that are emission of mass and are absorbed by mass in a similar way as electromagnetic waves might be a wrong preposition. Some researches exclude existence of gravitational waves that travel from stellar object A to stellar object B in order to keep them together (5,6).

Dynamic Equilibrium of the Atemporal Universe Astronomical observations show that Active Galactic Nucleus (AGN) of our galaxy “eats” near stars and galaxies and time by time throws out huge amount of fresh gas (7). AGN transforms matter it into quanta of space. This process increases density of space into AGN. As by black stars and neutron binary stars gravitational waves are spreading into outer space also from AGN. When a huge amount of matter is entering AGN, density of gravitational field reaches certain maximum in a very short time. This sudden increasing of is a cause for a big explosion where gravitational quanta transform into elementary particles. After density turns below maximum value, explosion stops. AGN are “refreshing” fabric of the universe, they transform “old” matter into “fresh” matter and keep entropy of the universe constant. In the universe there is a permanent fluctuation of energy “matter-space-matter-space”. Sum of density of matter and gravitational density of space in a given volume of universe tends to be in equilibrium: . When there is an access of density matter will turn into space, where there is an access of density gravitational energy of space will turn into matter. Universe is a dynamic system in a permanent dynamic equilibrium, there is no beginning and on end of the universe. References: [1] Einstein A., Relativity: The Special and General Theory (1920), page 155 http://​​www.bartleby.com/​​173/​​ [2] Yourgrau P. (2006) A World Without Time: The Forgotten Legacy of Gödel And Einstein [3] Sorli A., Sorli K. (2005) From Space-time to A-Temporal Physical Space, Frontier Perspectives, Vol. 14, Num. 1. [4] Fiscaletti D., Sorli A. (2005). Toward an a-temporal interpretation of quantum potential. Frontier Perspectives, Vol. 14, Num. 2.

[5] Sorli A., Sorli I. (2005). A-Temporal Gravitation And Hypothetical Gravitational waves, Electronic Journal of Theoretical Physics, Vol 2, Num 5 [6] Loinger A. The gravitational waves are fictitious entities – II http://​​arxiv.org/​​vc/​​astro-ph/​​papers/​​9904/​​9904207v1.pdf [7] Goss. W.M. (2003). Sagittarius A* as an AGN http://​​adsabs.harvard.edu/​​abs/​​2003ASPC..300..123G

[Ian_Maxwell]

If I understand this model correctly, it has the consequence that from a typical point in the configuration space there are not only many futures (i.e. paths starting at this point, along which entropy is strictly increasing), but many pasts (i.e. paths starting at this point, along which entropy is strictly decreasing). Does this sound correct?

[Zhaochen_He]

Question:

Doesn’t the multi-worlds interpretation of quantum mechanics define an arrow of time?

Imagine we have a random number generator which randomly adds or subtracts 1 from a given number, each with equal probability. Say our initial number is zero. After the first iteration, the space of possible values consists of {-1,1}. After two iterations, it expands to {-2,-1,0,1,2}. It seems clear that progressively larger iterations monotonically increase the space of possible outcomes. Doesn’t this defines an arrow of time in the forward direction?

Likewise, suppose our universe comes into existence with some initial state, S(0). As you suggest in your article, this state can by fully specified by phi(r), knowing the configuration over space of all particles and potentials.

From this point, the universe will evolve (again, as you have suggested in your article). As it does, the space of possible configurations for the universe increases; however, at any given time, some configurations are not yet accessible, as they constitute a greater change than one which could have happened (across all possible states) in the time elapsed since S(0).

Ok, one could object. But this assumes that the universe can only change in finitely sized steps (like the random adding machine mentioned earlier). But with quantum mechanics, there is no such limitation; ie, across any physical dimension (that is, value of a observable quantity), an arbitrarily large change is always possible, albeit with increasingly varnishing odds.

Ok. Fine. Consider then, the probability that a change of given size has come to pass. For a change of a fixed size, this probability increases as the system evolves. Again, an arrow of time is specified.

Couldn’t we define time along these lines? And if we did, wouldn’t that establish a difference between, say, two worlds with exactly the same physical configuration of particles, one which occurs at a later time, and one which occurs at an earlier time?

[amrit]

Temporal and Atemporal (Timeless) Experience of Motion

Motion runs in timeless space. Ordinary we experience it through psychological time. This experience is in time, temporal and indirect. Information of motion between perception and experience is broken.

motion—perception (eyes)- mind elaboration (in psychological time)- temporal experience

Once we become aware of psychological time we can experience motion directly as it runs in timeless space. This experience is atemporal (timeless) and direct. Information of motion between perception and experience is unbroken.

motion—perception (eyes) - atemporal experience

Development of atemporal experience is essential for further development of science. It gives a scientist an objective view about timeless nature of physical world. Temporal experience is subjective in a sense that passes through psychological time of the scientist. Atemporal experience is objective in a sense that information of motion between perception and experience is unbroken.

see more on
http://​​www.fqxi.org/​​data/​​forum-attachments/​​1_TIME_IS_RUN_OF_CKLOCKS__Sorli_2009.pdf

yours amrit

[amritsorli]

Barbour is right: universe is timeless

http://​​vixra.org/​​author/​​Amrit_S__Sorli

He is wrong by saying time does not exist. TIME IS RUN OF CLOCKS IN TIMELESS UNIVERSE

yours amrit

[hwc]

Wait, you have to keep t as a formal variable so you can take a partial derivative w.r.t. it.

[imaxwell]

Years after first reading this, I think I’ve internalized its central point in a clear-to-me way, and I’d like to post it here in case it’s useful to someone else with a similar bent to their thinking.

Without worrying about the specific nature of the Schrodinger equation, we can say the universe is governed by a set of equations of form x[i] = fi, where each x[i] is some variable in the universe’s configuration space, each f[i] is some continuous function, and t is a parameter representing time. This would be true even in a classical universe—the configuration space would just look more like the coordinates for a bunch of particles, and less like parameters of a waveform. All this is really saying is that the universe has some configuration at every time.

Now, one thing you can do with parametric equations is eliminate the parameter. If we have, say, 1000 parametric equations relating x[1] through x[1000] to t, we can convert these to 999 equations relating x[1] through x[1000] to one another, and “cut out the middleman” so to speak. Your new equations will define the same curve in configuration space, and you can determine the relative order of events just by tracing along that curve (as long as there are no “singularities”—points where two different values of t gave you the same point in the configuration space).

Moreover, from inside the universe there’s no way to tell the difference between these two situations. “Two hours ago” can mean either “at t − 2hr” or it can mean “at the point on this curve in configuration space where the clocks all say it’s 7:00 instead of 9:00”, and there’s no experimental distinction to be made between these meanings. So positing a fundamental thing called “time” doesn’t actually have any explanatory power!

From this understanding, timeless physics is better viewed as a more parsimonious way to frame any theory, rather than a part of quantum theory specifically. We could just as well explain Newtonian physics timelessly.

[jesch]

I also understood this using parametric equations, although I simplified to t, x(t) and y(t), to aid in visualization. So then I was looking at my mental image, and I thought “but what About memory?” At any particular point on my curve, the observer in that point knows what the curve looks like in one direction(past), but not the other. I get that both directions along the curve are determined, but why would my mind contain information about exactly one?

[imaxwell]

This is off the top of my head, so it may be total bullshit. I find the idea of memory in a timeless universe slippery myself, and can only occasionally believe I understand it. But anyway...

If you want to implement a sort of memory in your 2D space with one particle, then for each point (x0,y0) in space you can add a coordinate n(x0,y0), and a differential relation

dn(x0,y0) = δ(x-x0,y-y0) sqrt(dx^2 + dy^2)

where δ is the Dirac delta. Each n(x0,y0) can be thought of as an observer at the point (x0,y0), counting the number of times the particle passes through. There is no reference to a time parameter in this equation, and yet there is a definite direction-of-time, because by moving the particle along a path you can only increase all n(x0,y0) for points (x0,y0) along that path.

A point in this configuration space consists of a “current” point (x,y), along with a local history at each point. If you don’t make any other requirements, these local histories won’t give you a unique global history, because the points could have been visited in any order. But if you impose smoothness requirements on x and y, and your local histories are consistent with those smoothness requirements, then you will have only one possible global history, or at most a finite number.

[jiohdi]

one small problem, nothing is moving. how can you have an observer when every bit of that observer is part of the existing static universe… observer implies a moving entity and no motion exists in a static universe.

[handoflixue]

Do the classical equations, using ψ(r, t), assume that you’ll get a different outcome from ψ(r, n)? That is, if the system is in the exact same configuration, but at a “different time”, would the classical equations suggest a different outcome?

(Mostly, this struck me as another approach for demonstrating that this ‘t’ thing is extraneous.)

[Eliezer Yudkowsky]

Of course not.

[xelxebar]

This post inpires wtf moments in my brain. Anyone here read Greg Egan’s Permutation City?

Now I find myself asking “What is going on where I feel like there is this quantity time?” instead of “What is time?”

[lime]

Zero background in physics here. But these essays (or what little I understand of them) are blowing my mind. Here I’m going to ramble and ask questions. I would be so happy if somebody could enlighten me in some way.

I believe I understand the concept of configuration space (the pyramid diagram). But what does it means for an unchanging “quantum mist” to be distributed across this space? Is the mist denser in some areas than in others? Are the denser areas more probable configurations of matter? Are there some points within the space that the mist does not touch, and if so, are those configurations of matter impossible? Why is the mist distributed as such? (I realize that last question has no answer.)

It seems like there are two extreme configurations: the first one has all particles in the universe occupying the same space (the Big Bang; complete order), and the second has all particles in the universe equally spaced from one another, like in a crystal lattice or something (full entropy/​disorder). Could this be where the universe appears (to human brains) to be headed?

Side note: when I think about Einstein, this configuration space stuff makes sense. All particles in the universe must advance from one configuration to another at the same “global rate of motion.” That explains why time, as we know it, slows down for particles that move through space (or pass from one configuration to another) more quickly than other particles. Those fast-moving particles must “wait”, in a sense, for the slower-moving ones to catch up, so that all particles may retain the “global rate of motion”. Does that make sense? I might have just reiterated what was already said above...

Back to this mist. So do all configurations of matter (that the mist touches) exist at once? Do more probable configurations (dark mist) exist to a larger degree than less probable configurations (light mist)? Is that one of the ideas behind quantum mechanics? That configurations of matter can exist to different degrees?

What if we consider a photon instead of a particle? Photons move at the speed of light, where time stops. So do photons “see” all configurations of matter at once?

Not sure if these questions even make sense. Help!

[lukeprog]

Timelessness is one of the first things I grokked after accepting physicalism. After removing magic from my ontology, but before encountering Kolmogorov/​Solomonoff, I intuitively had the feel that the idea of a line called the ‘present’ that is constantly ‘moving forward’ and destroying everything before it and creating everything just ahead of it seemed astonishingly complicated and unnecessary. Minkowski spacetime doesn’t need time to be ‘moving’; that’s an unnecessary additional hypothesis. Our brains can ‘see’ the past and not the future because of the way memories are constructed in brains, which are part of the timeless physics.

[Mitchell_Porter]

This can’t be the right answer. Time does flow, whether or not you understand how that can be. This approach is like being troubled over why the universe exists—how can existence itself have a cause, when such a cause must already exist? - and obtaining relief by convincing yourself that nothing actually exists.

That things happen is bedrock knowledge about the world, up there with the knowledge that anything exists at all. You reject the idea that the present is a moving line which erases the past and creates the future? Fine, so do I. Past, present, and future coexist “in eternity”, but they all have the character of “becoming”, not just of “being”. There is a flow of time inside each world-line; the experience of your life is the feeling of the flow interior to the world-line of the conscious part of your brain. There is no point of awareness that moves along the line, erasing the past and creating the future; the line itself is the flow that occurs within the “eternal now” of your consciousness, from the moment it begins to exist, until the moment that it ceases to exist.

Maybe this is what you already meant by timelessness, but I don’t think so, especially since, in this post, Eliezer is advocating Julian Barbour’s ontology, in which the very idea of a world-line is an illusion, because there is no notion of space-time history as such, just a set of static, mutually detached spatial configurations.

[jiohdi]

I think you are close but still wrong. past and future only exist in the mind, not in reality. the past is just data about where stuff got recorded by you and has moved on to where it is now. the future is just an educated guess as to where that stuff will move to from here. NOW alone is real, NOW alone contains mass and energy. the only way we can experience and evolving time is because stuff is in motion and we have the capacity to record and project its locations. Time is a measure of changing relationships between matter and energy that exists and is in motion. 5 years ago means that the stuff of the universe has changed relationships and one of those relationships was the rotation of our planet around our sun 5 times. if the past present and future all exists then there is NOTHING moving and no way to notice anything change unless by some entity beyond it all, like a person watching a static film that moves via an external projector. if you accept that possibility that we are part of reality and not beyond it, then you cannot explain our perception of motion without actual motion involved.

[jiohdi]

TIME is not moving, its the measure of stuff like matter and energy moving. to say we can see the past but not the future because of the way memories are constructed implies motion which your blockhead universe sorely lacks. timeless physics ignores the implicit motion required for anyone to notice anything changing. if all moments were equally real that there is no way to say any moment is the present moment, the past or the future. no one would be moving to notice any other changes because there are not any actual changes going on. if all moments are real, you would have to be outside looking in on them to make the required motion.

[[deleted]]

I wish someone would make this into a talk and go around the country teaching it to high school students to force them to start to have deeper thinking. Eliezer’s explanation is wonderfully understandable. However, would it be possible to explain the time reversibility of the Schrödinger equation with simplified math to high school students?

[Grognor]

I understand that imposing a “fundamental time” on the universe creates no new predictions and is a totally redundant entity, to be eradicated in any elegant theory of physics -

But this does not resolve my confusion whatsoever when I find myself asking, “What happened before the big bang? What is the universe expanding into?” “Nothing,” is certainly insufficient. “Nothing” has no properties, and “able to be expanded into” is a property. In any case, answering “nothing” does not dissolve the question, and “nothing” is merely a teacher’s password anyway.

I’m confident that somewhere, somehow, I’m making a buried assumption or misunderstanding something somewhere. I just have no clue where that might be.

I’ve long ago dissolved all notions of a “self” given unto me as a real entity with empirical consequences, and I now find this intuitively obvious and can no longer imagine a world where there’s a “fundamental self”. So why can’t I do the same thing with a “fundamental time”?

[kilobug]

If Time is, as Julian Barbour postulates, not a fundamental component of physics, but an illusion created by relative configuration of matter that embed history (as in, memories in brains, fossils in the soil, …), then “What happened before the big bang?” doesn’t have any more meaning than “What happens before the beginning of a book?” or “What is north of the north pole?”.

If configuration space just is (not “always” because time doesn’t exist at the level of configuration space, only inside individual configuration), and the Big Bang is just an edge of it, it doesn’t have any meaning to ask “What happened before the big bang?” as it doesn’t make any sense to ask what lies beyond the corner of the pyramid in triangle land.

[Grognor]

Nitpick: “What happens before the beginning of a book?” is actually a meaningful question, or else prequels would have a hard time existing.

As before, though, I understand that “before the big bang” doesn’t actually make sense, but then saying “it doesn’t make sense” or “it’s like trying to guess what’s north of the north pole” are, respectively, a teacher’s password and an analogy. Passwords are useless, and analogies help in understanding only if an institutive intuition is already there. As an analogy, I’d say that an analogy only helps propagate an already held belief through a shoddy barely-Bayesian belief network. (In fact, that’s good. I should keep that.)

Your comment is helpful, though. I think, now, that I’ve framed the problem enough that it will slowly dissolve on its own. (This is a question of my own psychology and not one of underlying reality, after all.) It still feels strange, though, at the moment… though it does look increasingly likely that I’m confusing “time before the big bang” with “what caused the big bang”, which, if I understand correctly, is a much harder problem.

[duckduckMOO]

Does each axis in the first configuration space diagram correspond to a list of all possible positions of the particle in 2d space (with each given a numerical label that allows for the axis to go from one upwards as is normal for graphs)?

Thanks

[Zaq]

A coupleof things:

1. You begin by describing time translation invariance, even relating it to space translation invariance. This is all well and good, except that you then you ask:

“Does it make sense to say that the global rate of motion could slow down, or speed up, over the whole universe at once—so that all the particles arrive at the same final configuration, in twice as much time, or half as much time? You couldn’t measure it with any clock, because the ticking of the clock would slow down too.”

This one doesn’t make as much sense to me. This is not just a translation but is actually a re-scaling. If you rescale time separately from space then you will have problems because you will qualitatively change the metric (special relativity under t → 2t no longer uses a minkowski metric). This in turn changes the geometric structure of spacetime. If you rescale both time and space then you have a conformal transformation, but this transformation is not a lorentz transformation. I’m not so sure physics is invariant under such transformations.

1. The electroweak force has been observed to violate both charge conjugation symmetry and parity symmetry. However, any lorentz invariant physics must be symmetric under CPT (charge conjugation + parity + time reversal). Thus if our universe is lorentz invariant, it is not time-reversal invariant. So you will at least need to keep the direction of time, even if you are able to otherwise eliminate t.

“@Stirling: If you took one world and extrapolated backward, you’d get many pasts. If you take the many worlds and extrapolate backward, all but one of the resulting pasts will cancel out! Quantum mechanics is time-symmetric.”

Um… no. As I explained above, lorentz invariance plus CP violation in electroweak experiments indicate that the universe is not invariant under time-reversal. http://​​en.wikipedia.org/​​wiki/​​CP_violation

Eh… correction. Quantum Mechanics may be time-symmetric, but quantum field theories including weak interactions are not.

[Oscar_Cunningham]

Does it make sense to say that the global rate of motion could slow down, or speed up, over the whole universe at once—so that all the particles arrive at the same final configuration, in twice as much time, or half as much time? You couldn’t measure it with any clock, because the ticking of the clock would slow down too.

This one doesn’t make as much sense to me. This is not just a translation but is actually a re-scaling. If you rescale time separately from space then you will have problems because you will qualitatively change the metric (special relativity under t → 2t no longer uses a minkowski metric). This in turn changes the geometric structure of spacetime. If you rescale both time and space then you have a conformal transformation, but this transformation is not a lorentz transformation. I’m not so sure physics is invariant under such transformations.

If you change the value of c as you scale time then physics will stay the same.

[Zaq]

Uh… what?

c is the speed of light. It’s an observable. If I change c, I’ve made an observable change in the universe --> universe no longer looks the same?

Or are you saying that we’ll change t and c both, but the measured speed of light will become some function of c and t that works out to remain the same? As in, c is no longer the measured speed of light (in a vacuum)? Then can’t I just identify the difference between this universe and the t → 2t universe by seeing whether or not c is the speed of light?

I also think you’re stuck on restricting yourself only to E&M using Special Relativity. If you take t → 2t you change the metric from minkowski space to some other space, and that means that you’ll have gravitational effects where there previously weren’t gravitational effects. You might be able to salvage that in some way, but it’s going to be a lot more complicated than just changing the value for c. The only thing I can think of is to re-define the 4-vector dot-product and the transformation laws for objects with Lorentz indeces, and even that might not end up being consistent.

[Oscar_Cunningham]

This post just got a shout-out on Dinosaur Comics!

[ESRogs]

Which part of this is not standard physics?

[Oscar_Cunningham]

The part where he gets rid of the t coordinate?

[SoopaHotFya]

I have several questions because this is a fair bit over my head. Are you arguing that time is a state of observing an action? If this is the case then what is the state of the universe without life, an observer?

[[deleted]]

While I don’t disagree with the main conclusion, I have a problem with the following quote: “The r never repeats itself. The universe is expanding, and in every instant, it gets a little bigger. We don’t need a separate t to keep things straight. When you’re looking at the whole universe, a unique function ψ of (r, t) is pretty much a unique function of r.” The permanent expansion is just some property our universe happens to have, that one could argue is a function of your abstract time variable. Suppose there existed a physical clock somewhere (similar to our human clocks) that was created during the big bang, you could replace “The universe is expanding” by “The clock keeps changing”—just as a proxy of abstract time. So the above paragraph does not add anything useful to the argument?

[jiohdi]

not to mention that the original t was a marker used by a sentient beings to order his experiences and by saying r contains all experiences and so we don’t need t any more is false. r does not in any way replace or make redundant the original use of t.

[rthomas2]

Regarding the idea of “changing the future” invoked by the Majere quote:

The concept here relies upon some notion of causality. In order for it to be coherent, we have to think of the past and future as being determined—that if we knew both the state of the universe at a given time, and the laws of physics, we could calculate every other state the universe would ever have, or had ever had previously.

This conception doesn’t really seem to jive with what very, very little I know about many worlds and quantum mechanics, so it could be utterly false. That said, to understand the Majere quote, we have to refer to this particular conception, because it’s the one Majere’s assertion derives from.

The idea that we are “changing the future” comes from a formulation of the idea of free will. The basic idea is that, given the idea of a deterministic universe just established, the future is set, and all we do is watch it unfold from inside our heads. That is, except if we happen to be, as Majere thinks, creatures who possess Majere’s idea of free will.

In that case, we have the power to alter ourselves to a degree, and thus, alter the present state of the universe—and thereby, its future states. And further, this power is “free”—it is in no way influenced by causality. This last may seem impossible, and it probably is. But it’s the assumption which the idea of free will rests upon—that there is some force, usually asserted to be spiritual in nature, that is “above” the material world; by unspecified means, this force can alter the natural world without being causally determined by it. It’s outside of the system, so to speak, and yet able to interact on its own terms.

This idea, as I’ve said, seems absurd given our knowledge of physics. That said, it is clearly the one Majere assumes. It is by this conception that, given the same physical state of the world, we could not predict exactly what would happen next—for there is no telling what choices beings of free will may make, and indeed, if somehow the same creatures might come to the same state of the same universe a second time, they could theoretically choose something entirely different.

[A1987dM]

“You’d be arrested for violating the laws of physics.”

LOL.

[zslastman]

Where does all this leave causation in Pearl’s sense of the term? Don’t we still need to specify a time axis so that we can express our conditional probabilities correctly?

[Eliezer Yudkowsky]

See “Timeless Causality”: http://​​lesswrong.com/​​lw/​​qr/​​timeless_causality/​​

[linkhyrule5]

… On a slightly random note, this reminds me of Neal Stephenson’s Anathem’s Hemn space, and the idea of a universe as a particular path through configuration space.

Anyway. There’s a flaw in your gedankenexperiment, when you stop time across every galaxy, and I’m wondering if you have a response. Namely, relativity—in particular, simultaneity.

Essentially: When you “stop time,” you’re saying: “From my perspective, everything simultaneous to me remains so; if I were to assign to myself a “simulation step function”, I could step forward without noting any change in my surroundings.”

(This is not rigorous, because my understanding of GR is not rigorous; nevertheless, I think I have enough of a conceptual understanding to use it in this manner.)

(Also because you can’t stop time.)

Anyway. This has a flaw, in that any moving object will see other objects rotated through spacetime; “stopping time” relative to that moving object will result in a universe that evolves relative to a stationary object (relative to some lab frame.) So you can’t actually stop time across the entire universe; bits of the universe will just suddenly hang still. If the universe is running on a computer somewhere, you could tell it to not move to the next step, but I’m not at all sure what that would do.

I’m not sure how critical this is to the core argument, but you might at least want to change the thought experiment.

(On a side note—I made a Minkowsky diagram while thinking this through, so have a look if you want.)

(On an extra side note—I notice that most of the new replies have been added to the bottom of this list, but mine has been added to the top. A), is this something I should be doing, and B), how do I determine where my posts go?)

[linkhyrule5]

Restating, now that I’ve written all that out and my mind is clearer: the fundamental problem is that there’s no absolute time to stop. Your galaxies wouldn’t stop rotating, they’d spin apart about whatever point you decided to take your volume of simultaneity from.

[physicsgrad]

Sorry to be pedantic, but I have to take exception to the line:

“when Einstein disproved Newton’s theory of gravity”

This is at best a misrepresentation of the nature of science, and at worst a total misunderstanding. Einstein absolutely did not disprove Newton—his Relativity superseded Newton’s Laws of Gravitation, but at the same time encompassed them as a special case of Relativity (when Relativity is simplified by reducing velocities to “everyday” speeds, i.e. tiny fraction of fraction of the speed of light).

[DavidPlumpton]

It seems there may actually be some experimental evidence in this area, https://​​medium.com/​​the-physics-arxiv-blog/​​d5d3dc850933 with the experiment details at http://​​arxiv.org/​​abs/​​1310.4691

It blows my mind that there could be anything experimentally detectable, even in principle.

[Mitchell_Porter]

Suppose you carry a timetable of your daily routine with you. Whenever you look at the whole timetable, it’s the same; but if you just look at a random single line of the timetable, there’s a “clock observable” (words saying what time it is) and a “state of the universe observable” (words saying what activity should be happening at that time).

This experiment is “evidence” for the emergence of time from entanglement, to exactly the same degree that the experiment I just described, of looking at your daily schedule, is evidence for time being relational. They have a global superposition which remains the same over time, but in which the observed state of one part is correlated with the observed state of the other part.

The “physics arxiv blog” (which has no official relation to arxiv, it’s just someone describing random papers) is completely uncritical, and faithfully repeats whatever claims authors make about the meaning of their work.

[DavidPlumpton]

So it sounds like you’re saying the details may all be correct but the high level interpretation of the results is significantly overreaching. Not too unexpected, I guess.

[Psychosmurf]

I don’t think this is anything really new. The principle of general covariance in GR says that the laws of physics should remain invariant under a diffeomorphism. Since coordinate transformations are diffeomorphisms, and since time is relative, the equations of GR do not depend on time. Indeed, I think the search for a background independent theory of quantum gravity is exactly the approach taken by Loop Quantum Gravity.

[mauriciozuardi]

Cannot stop picturing this ”.. timeless mathematical object ..” as something like this: http://​​laughingsquid.com/​​hey-jude-flow-chart/​​ – the only difference is that every point in the chart is a still frame of the universe.

Interesting that this “reality” configuration is very “user-friendly”: a unlimited number of “sentient-beings” can read the chart at the same time with little or no impact to the system. And if we see one’s “life” as is it’s own reading path, we have an interesting –and elegant– picture of the “implementation” of the multiple universes theory.

Multiple versions of me can be at the exact same “frame” at the same time, but it holds a different “meaning” inside their own reading path, the exact same way that the same word can mean different things between two different words.

Just letting my mind run wild.

[wafflepudding]

An omnipotent magicker decides to flip a coin, and the coin lands heads. Afterwards, the magicker changes every particle in the universe to what it would be had the coin landed tails—including those in his own brain. Is it true that in the past, the coin landed heads, even though this event is epiphenomenal?

I realize that the magicker is violating the laws of entropy, and that in the real world there are no magickers. I also realize that for the purposes of anyone in the universe, the first coin flip doesn’t and couldn’t possibly matter, because it was epiphenomenal. But I’m still curious what the answer to my question is.

[hairyfigment]

It may help to start with regular quantum mechanics/​ Many Worlds. Because there, your scenario sounds like a world receiving amplitude from two different histories—actually many more, but let’s start with them—there’s the actually possible history in which the coin landed tails, and the magical one where it landed heads. Both contribute to the underlying result.

Timeless physics sounds like it takes this one step further. In this view, both pasts exist as disconnected points in a timeless space. Eliezer’s version (I think) has an implicit causal connection between the ‘present’ and the ‘tails’ past if we analyze them according to real physics, and another connection to ‘heads’ if we analyze them by magical physics.

[mamert]

For the purposes of the universe, the first coin flip not only doesn’t matter, it never existed. The magicker himself will claim—and show any amount of supporting evidence—that it landed tails. He will not even remember casting a spell, unless he’d have cast one in this case, too, but for a different reason (if he’d have cast anyway regardless of the toss outcome, he’d get looped, recalling himself making the toss, but not yet casting; or being confused why he recalls casting, but there is no change in the toss outcome).

Time between the toss and casting, when things were different than they are now? What perspective would that need? Looking at the universe from outside the universe?

[markpalenik]

I’m sorry, but this is stupid. It’s not something “being taken seriously by todays physicists” and quite frankly, this article doesn’t really say anything at all.

First of all, classical physics isn’t exactly a “wrong” model of physics. Newton’s laws are still obeyed in quantum mechanics, but as operator equations on the X and P operators in the Hilbert space. The only difference is that X and P, instead of being numbers, are non-commuting operators.

Second, lets look at the Schrodinger equation a little more closely. In it, time and space AREN’T treated on equal footing, so it doesn’t simply make sense to parametrize r as a 4 vector. You have SECOND derivates of space and only FIRST derivatives of time.

Actual physics—relativistic physics—is covariant, which means that particles and fields transform under the Lorentz group. In the Klein-Gordan and Dirac equations (and Maxwell’s equations), time and space ARE treated on equal footing because they can Lorentz-transform into one another. So, space and time are part of a 4 vector. But this IS mainstream physics and has been mainstream physics for 90 years or so.

I realize I’ve gotten way too outraged over this, but I just finished reading Chapter 28 and the top of Chapter 29 in “Harry Potter and the Methods of Rationality”, and googled “Similarly, timeless formulations of quantum mechanics” to figure out what the hell you were talking about (and I have a PhD in physics. My research is in quantum chemistry/​density functional theory).

[Дмитрий Зеленский]

Either I have my math wrong, or there’s nothing wrong with saying that there is a function F(r,t(r)) where t(r) is a function read off r which signifies… well, time. And while F(r,t(r)) is a function of r, it may be more useful for some problems to have it as initially written not F’(r) (for example, because t(r) may have an obvious GLUT).

[Dexter McSnuggles]

Is any of this falsifiable? If it’s not, why does this theory have more weight than saying that time goes in reverse? Or that time jumps around at random? What difference would it make if we accepted this as reality?