Decoherence
Previously in series: Feynman Paths
To understand the quantum process called “decoherence”, we first need to look at how the special case of quantum independence can be destroyed—how the evolution of a quantum system can produce entanglement where there was formerly independence.
Reluctant tourists visiting quantum universes think as if the absence of a rectangular plaid pattern is some kind of special ghostly link between particles. Hence the unfortunate term, “quantum entanglement”.
The evolution of a quantum system can produce entanglement where there was formerly independence—turn a rectangular plaid pattern into something else. Quantum independence, being a special case, is easily lost.
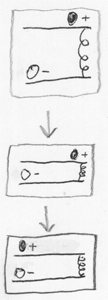
At right is a system in which a positively charged light thingy is on a track, far above a negatively charged heavy thingy on a track.
At the beginning, the two thingies are far enough apart that they’re not significantly interacting.
But then we lower the top track, bringing the two thingies into the range where they can easily attract each other. (Opposite charges attract.)
So the light thingy on top rolls toward the heavy thingy on the bottom. (And the heavy thingy on the bottom rolls a little toward the top thingy, just like an apple attracts the Earth as it falls.)
Now switch to the Feynman path integral view. That is, imagine the evolution of a quantum system as a sum over all the paths through configuration space the initial conditions could take.
Suppose the bottom heavy thingy and the top thingy started out in a state of quantum independence, so that we can view the amplitude distribution over the whole system as the product of a “bottom thingy distribution” and a “top thingy distribution”.
When we lower the top track, the light thingy on top is attracted toward the heavy bottom thingy -
- except that the bottom thingy has a sub-distribution with three bulges in three different positions.
So the end result is a joint distribution in which there are three bulges in the amplitude distribution over joint configuration space, corresponding to three different joint positions of the top thingy and bottom thingy.
I’ve been trying very carefully to avoid saying things like “The bottom thingy is in three places at once” or “in each possibility, the top thingy is attracted to wherever the bottom thingy is”.
Still, you’re probably going to visualize it that way, whether I say it or not. To be honest, that’s how I drew the diagram—I visualized three possibilities and three resulting outcomes. Well, that’s just how a human brain tends to visualize a Feynman path integral.
But this doesn’t mean there are actually three possible ways the universe could be, etc. That’s just a trick for visualizing the path integral. All the amplitude flows actually happen, they are not possibilities.
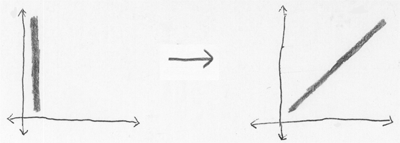
Now imagine that, in the starting state, the bottom thingy has an amplitude-factor that is smeared out over the whole bottom track; and the top thingy has an amplitude-factor in one place. Then the joint distribution over “top thingy, bottom thingy” would start out looking like the plaid pattern at left, and develop into the non-plaid pattern at right:
Here the horizontal coordinate corresponds to the top thingy, and the vertical coordinate corresponds to the bottom thingy. So we start with the top thingy localized and the bottom thingy spread out, and then the system develops into a joint distribution where the top thingy and the bottom thingy are in the same place, but their mutual position is spread out. Very loosely speaking.
So an initially factorizable distribution, evolved into an “entangled system”—a joint amplitude distribution that is not viewable as a product of distinct factors over subspaces.
(Important side note: You’ll note that, in the diagram above, system evolution obeyed the second law of thermodynamics, aka Liouville’s Theorem. Quantum evolution conserved the “size of the cloud”, the volume of amplitude, the total amount of grey area in the diagram.
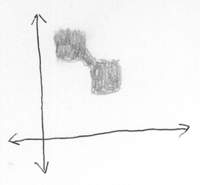
If instead we’d started out with a big light-gray square—meaning that both particles had amplitude-factors widely spread—then the second law of thermodynamics would prohibit the combined system from developing into a tight dark-gray diagonal line.
A system has to start in a low-entropy state to develop into a state of quantum entanglement, as opposed to just a diffuse cloud of amplitude.
Mutual information is also negentropy, remember. Quantum amplitudes aren’t information per se, but the rule is analogous: Amplitude must be highly concentrated to look like a neatly entangled diagonal line, instead of just a big diffuse cloud. If you imagine amplitude distributions as having a “quantum entropy”, then an entangled system has low quantum entropy.)
Okay, so now we’re ready to discuss decoherence.
The system at left is highly entangled—it’s got a joint distribution that looks something like, “There’s two particles, and either they’re both over here, or they’re both over there.”
Yes, I phrased this as if there were two separate possibilities, rather than a single physically real amplitude distribution. Seriously, there’s no good way to use a human brain to talk about quantum physics in English.
But if you can just remember the general rule that saying “possibility” is shorthand for “physically real blob within the amplitude distribution”, then I can describe amplitude distributions a lot faster by using the language of uncertainty. Just remember that it is language. “Either the particle is over here, or it’s over there” means a physically real amplitude distribution with blobs in both places, not that the particle is in one of those places but we don’t know which.
Anyway. Dealing with highly entangled systems is often annoying—for human physicists, not for reality, of course. It’s not just that you’ve got to calculate all the possible outcomes of the different possible starting conditions. (I.e., add up a lot of physically real amplitude flows in a Feynman path integral.) The possible outcomes may interfere with each other. (Which actual possible outcomes would never do, but different blobs in an amplitude distribution do.) Like, maybe the two particles that are both over here, or both over there, meet twenty other particles and do a little dance, and at the conclusion of the path integral, many of the final configurations have received amplitude flows from both initial blobs.
But that kind of extra-annoying entanglement only happens when the blobs in the initial system are close enough that their evolutionary paths can slop over into each other. Like, if the particles were either both here, or both there, but here and there were two light-years apart, then any system evolution taking less than a year, couldn’t have the different possible outcomes overlapping.
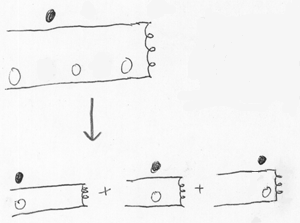
This diagram shows a blob of amplitude that factors into the product of a 2D subspace and a 1D subspace. That is, two entangled particles and one independent particle.
The vertical dimension is the one independent particle, the length and breadth are the two entangled particles.
The independent particle is in one definite place—the cloud of amplitude is vertically narrow. The two entangled particles are either both here, or both there. (Again I’m using that wrong language of uncertainty, words like “definite” and “either”, but you see what I mean.)
Now imagine that the third independent particle interacts with the two entangled particles in a sensitive way. Maybe the third particle is balanced on the top of a hill; and the two entangled particles pass nearby, and attract it magnetically; and the third particle falls off the top of the hill and rolls to the bottom, in that particular direction.
Loosely speaking, in the case where the two entangled particles were over here, the third particle went this way, and in the case where the two entangled particles were over there, the third particle went that way.
So now the final amplitude distribution is fully entangled—it doesn’t factor into subspaces at all.
But the two blobs are more widely separated in the configuration space. Before, each blob of amplitude had two particles in different positions; now each blob of amplitude has three particles in different positions.
Indeed, if the third particle interacted in an especially sensitive way, like being tipped off a hill and sliding down, the new separation could be much larger than the old one.
Actually, it isn’t necessary for a particle to get tipped off a hill. It also works if you’ve got twenty particles interacting with the first two, and ending up entangled with them. Then the new amplitude distribution has got two blobs, each with twenty-two particles in different places. The distance between the two blobs in the joint configuration space is much greater.
And the greater the distance between blobs, the less likely it is that their amplitude flows will intersect each other and interfere with each other.
That’s decoherence. Decoherence is the third key to recovering the classical hallucination, because it makes the blobs behave independently; it lets you treat the whole amplitude distribution as a sum of separated non-interfering blobs.
Indeed, once the blobs have separated, the pattern within a single blob may look a lot more plaid and rectangular—I tried to show that in the diagram above as well.
Thus, the big headache in quantum computing is preventing decoherence. Quantum computing relies on the amplitude distributions staying close enough together in configuration space to interfere with each other. And the environment contains a zillion particles just begging to accidentally interact with your fragile qubits, teasing apart the pieces of your painstakingly sculpted amplitude distribution.
And you can’t just magically make the pieces of the scattered amplitude distribution jump back together—these are blobs in the joint configuration, remember. You’d have to put the environmental particles in the same places, too.
(Sounds pretty irreversible, doesn’t it? Like trying to unscramble an egg? Well, that’s a very good analogy, in fact.
This is why I emphasized earlier that entanglement happens starting from a condition of low entropy. Decoherence is irreversible because it is an essentially thermodynamic process.
It is a fundamental principle of the universe—as far as we can tell—that if you “run the film backward” all the fundamental laws are still obeyed. If you take a movie of an egg falling onto the floor and smashing, and then play the film backward and see a smashed egg leaping off the floor and into a neat shell, you will not see the known laws of physics violated in any particular. All the molecules will just happen to bump into each other in just the right way to make the egg leap off the floor and reassemble. It’s not impossible, just unbelievably improbable.
Likewise with a smashed amplitude distribution suddenly assembling many distantly scattered blobs into mutual coherence—it’s not impossible, just extremely improbable that many distant starting positions would end up sending amplitude flows to nearby final locations. You are far more likely to see the reverse.
Actually, in addition to running the film backward, you’ve got to turn all the positive charges to negative, and reverse left and right (or some other single dimension—essentially you have to turn the universe into its mirror image).
This is known as CPT symmetry, for Charge, Parity, and Time.
CPT symmetry appears to be a really, really, really deep principle of the universe. Trying to violate CPT symmetry doesn’t sound quite as awful to a modern physicist as trying to throw a baseball so hard it travels faster than light. But it’s almost that awful. I’m told that
General RelativityQuantum Field Theory requires CPT symmetry, for one thing.So the fact that decoherence looks like a one-way process, but is only thermodynamically irreversible rather than fundamentally asymmetrical, is a very important point. It means quantum physics obeys CPT symmetry.
It is a universal rule in physics—according to our best current knowledge—that every apparently irreversible process is a special case of the second law of thermodynamics, not the result of time-asymmetric fundamental laws.)
To sum up:
Decoherence is a thermodynamic process of ever-increasing quantum entanglement, which, through an amazing sleight of hand, masquerades as increasing quantum independence: Decoherent blobs don’t interfere with each other, and within a single blob but not the total distribution, the blob is more factorizable into subspaces.
Thus, decoherence is the third key to recovering the classical hallucination. Decoherence lets a human physicist think about one blob at a time, without worrying about how blobs interfere with each other; and the blobs themselves, considered as isolated individuals, are less internally entangled, hence easier to understand. This is a fine thing if you want to pretend the universe is classical, but not so good if you want to factor a million-digit number before the Sun burns out.
Part of The Quantum Physics Sequence
Next post: “The So-Called Heisenberg Uncertainty Principle”
Previous post: “Three Dialogues on Identity”
- Where Physics Meets Experience by (25 Apr 2008 4:58 UTC; 68 points)
- The Quantum Physics Sequence by (11 Jun 2008 3:42 UTC; 65 points)
- Three Dialogues on Identity by (21 Apr 2008 6:13 UTC; 54 points)
- Collapse Postulates by (9 May 2008 7:49 UTC; 54 points)
- Timeless Physics by (27 May 2008 9:09 UTC; 53 points)
- The So-Called Heisenberg Uncertainty Principle by (23 Apr 2008 6:36 UTC; 31 points)
- And the Winner is… Many-Worlds! by (12 Jun 2008 6:05 UTC; 28 points)
- On Being Decoherent by (27 Apr 2008 4:59 UTC; 24 points)
- Spooky Action at a Distance: The No-Communication Theorem by (5 May 2008 2:43 UTC; 21 points)
- An Intuitive Explanation of Quantum Mechanics by (12 Jun 2008 3:45 UTC; 16 points)
- The Graviton as Aether by (4 Mar 2010 22:13 UTC; 15 points)
- Quantum Physics Revealed As Non-Mysterious by (12 Jun 2008 5:20 UTC; 13 points)
- Quantum Mechanics and Personal Identity by (12 Jun 2008 7:13 UTC; 12 points)
- 's comment on Overcoming the Curse of Knowledge by (18 Oct 2011 23:52 UTC; 7 points)
- 's comment on [SEQ RERUN] Fake Explanations by (29 Jul 2011 23:44 UTC; 7 points)
- [SEQ RERUN] Decoherence by (13 Apr 2012 5:15 UTC; 5 points)
- 's comment on [Link] New paper: “The quantum state cannot be interpreted statistically” by (18 Nov 2011 18:46 UTC; 4 points)
- 's comment on Why Many-Worlds Is Not The Rationally Favored Interpretation by (30 Sep 2009 23:28 UTC; 4 points)
- 's comment on Open Thread, December 1-15, 2012 by (1 Dec 2012 17:41 UTC; 2 points)
- 's comment on Open Thread, April 1-15, 2013 by (6 Apr 2013 21:18 UTC; 2 points)
- 's comment on Designing Rationalist Projects by (15 May 2011 17:06 UTC; -59 points)
CPT symmetry is required by Quantum Field Theory, not General Relativity.
If instead we’d started out with a big light-gray square—meaning that both particles had amplitude-factors widely spread—then the second law of thermodynamics would prohibit the combined system from developing into a tight dark-gray diagonal line.
What would the result look like, then? Amplitude would still flow towards configurations where the thingies are at the same horizontal position.
Not really. If both particles are widely-spread, then they will remain widely spread. Say the heavy particle is evenly distributed across the interval [0,2] and the light particle spread evenly across [0,3]. Then the resulting system will have both particles spread evenly across [0,2.0] (approximately; the large particle will move out somewhat), and the light particle will be approx. 50% more dense at each of those points.
Can that be made more precise? Obviously it is true in a purely topological sense, because amplitude distributions evolve according to a differential equation. But that doesn’t tell us how far away the blobs have to be for us to start seeing the effect. Can we put a metric on configuration space, and then get a theorem that says if 99% of the amplitude of psi1 is d units away from 99% of the amplitude of psi2 then the joint distribution evolves approachability like psi1 and psi2 would evolve in isolation, with a maximum error of whatever%?
I’m just now, belatedly, realizing that this means our linguistic tools for dealing with physical objects are among the big problems with quantum dynamics … which is interesting. There’s been a lot said and done regarding the ubiquity of spatial metaphors in language, which would partially explain why our intuitive grasp of quantum dynamics is ordinarily so poor.
OK, so now it’s pretty clear you’re committed to a many-worlds interpretation. When I’m done with your experiment, I don’t see two blobs, just one. Because there is a separate Bob-blob corresponding to each outcome.
I don’t think I quite follow why the individual blobs will tend to be rather more factorizable. Could someone clarify that for me? Thanks.
So how does this physically-real amplitude distribution, interface with our cognitive architecture? (Okay, maybe there’s a way to say that with smaller words...) Is it something like, “Any factorizable concentrated lump is interpreted as an object, everything else as an object randomly appearing between its high-amplitude-distribution places”? And what what method does the brain use to infer objects from out of the amplitude distribution?
So where do the probabilities come from? If there’s “an” electron that we’ve calculated has 1⁄4 of it’s amplitude here, and 3⁄4 of it’s amplitude across the street, and we have detectors set up in both places, then after the electron has interacted with the detectors and I’ve read their outputs there should be two big blobs of amplitude. One blob with 1⁄4 of the amplitude that represents I-who-saw-the-electron-here, and one blob with 3⁄4 of it that represents I-who-saw the-electron-across-the-street. Why shouldn’t I bet $1 for $2 if the electron is here? What difference does the amplitude make? I’m either one blob or the other.
Silas, it doesn’t interface with our cognitive architecture; our sensory organs don’t perceive amplitudes—in fact, AFAIK, nothing can. It happens at a more fundamental level—there are two blobs representing two different photon patterns (e.g.) headed towards your eyes, which interact with the one blob that is the previous state of your eyes and decohere it into two blobs that are your eyes sensing different things, which decoheres your brain… and at this point, I run into the same problem as Larry.
Nick_Tarleton: Silas, it doesn’t interface with our cognitive architecture … there are two blobs representing two different photon patterns (e.g.) headed towards your eyes, which interact with the one blob that is the previous state of your eyes and decohere it into two blobs that are your eyes sensing different things, which decoheres your brain
And that would count as interfacing with our cognitive architecture. Is it time to start tabooing words? Was my question not clear?
“what method does the brain use to infer objects” makes it sound like there are direct, contingent rules of interpretation embodied in the brain, rather than indirect, necessary relationships coming from outside the brain.
Nick_Tarleton: Then that would be different part of my post you’re now objecting to. First, you denied that there was an “interface” between the amplitude distribution and our cognitive architectures. Now, the part of my post you deem ill-posed, is the part where I ask about the brain “inferring objects”. And that’s a fair point, but at least try to be consistent about what part you deemed in error.
So, yes, it was perhaps too specific, or too anthropomorphic (!) to talk of the brain “inferring objects”. What I mean is, what is the mapping between amplitude distributions and my conscious experience of an object? I’m guessing Eliezer is going to answer that in later posts.
Eliezer: If instead we’d started out with a big light-gray square—meaning that both particles had amplitude-factors widely spread—then the second law of thermodynamics would prohibit the combined system from developing into a tight dark-gray diagonal line.
Nick: What would the result look like, then? Amplitude would still flow towards configurations where the thingies are at the same horizontal position.
This is confusing me too. Please can anyone clarify?
Eliezer: “you will not see the known laws of physics violated in any particular.” ← shouldn’t there be a “way” at the end of that?
Nick and Recovering,
Off the top of my head (I Am Not A Physicist), if you tried this in real life:
Imagine the light thingy starting out in many different positions. Now imagine the track is frictionless. The light thingy will swing back and forth over the heavy thingy, its exact position and orbit depending on its starting position.
Does the light thingy roll to a halt? There must be friction. Friction generates heat. Heat is entropy. One subspace may go from light gray to dark gray, but another subspace goes from dark gray to light gray, and the total amplitude density is conserved.
Also, the heavy thingy itself will move as the light thingy moves toward it; pulling forces are symmetrical, by conservation of momentum. If the heavy thingy is made up of lots of little particles, they all end up in slightly different places, depending on where the light thingy was originally.
I think you’re confusing classical probabilities with quantum amplitudes.
The classical case is what you describe. We start with a probability distribution in which the two particles are know to be stationary but they have uniform distributions for their starting positions. Then as the system evolves they get drawn closer together and so our uncertainty about their position goes down. But their momentum depends on their initial positions and so we gain uncertainty about their momentum. Thus the total entropy is conserved. (If we wish we can then use friction to shift the entropy into the heat degrees of freedom.)
But in the quantum case the amplitudes are assigned only to the configuration space of the particles i.e. to their positions. There is no momentum space into which we can put our spare entropy. In fact it is possible for quantum amplitudes to become tighter as time passes, even without any outside interference (this doesn’t contradict the Second Law because the Second Law is about our uncertainty about the wavefunction, not the spread-out-ness of the wavefunction itself). For example there are solutions of the Schrodinger equation for a free particle where a Gaussian wavepacket evolves into one with a smaller variance (of its associated “probability distribution”).
So I think you’re literally wrong when you say:
Because in the quantum case the light gray square isn’t representing a spread out probability distribution. We know exactly what the wavefunction is. The light gray square and the dark gray line both represent cases of total certainty! The time when entropy would come in would be if we had some Bayesian uncertainty about what the wavefunction actually was—a probability distribution on the space of amplitude assignments.
That makes sense—thank you :)
Great series, btw. You make QM feel true. I always felt at odds with explanations of it before now. I still feel missing parts of the puzzle pricking at my mind (most probably answered later so I’ll hold off on annoying questions), but the bits that are there actually fit.
Of course. How silly of me.
This also means that even when the distribution is initially a line, it’ll still lose entropy and become a thinner line.
Anyways, asking this again since it may have been buried via other commens: I’m still confused as to why the individual blobs would tend to be more factorable. Why would they factorize easily post decoherence?
“But the two blobs are more widely separated in the configuration space. Before, each blob of amplitude had two particles in different positions; now each blob of amplitude has three particles in different positions.
Indeed, if the third particle interacted in an especially sensitive way, like being tipped off a hill and sliding down, the new separation could be much larger than the old one.
Actually, it isn’t necessary for a particle to get tipped off a hill. It also works if you’ve got twenty particles interacting with the first two, and ending up entangled with them. Then the new amplitude distribution has got two blobs, each with twenty-two particles in different places. The distance between the two blobs in the joint configuration space is much greater.”
I’m not clear on why the amplitude involving more particles means that they’re further apart in configuration space. This probably shows I simply don’t understand configuration space, so sorry if the confusion links to a previous post! Thanks for any help, and please bear in mind I’m not science educated and relying on pre-university maths only...
I don’t know what metric (method of measuring distance) you use for configuration space. But assume it’s the standard, familiar Euclidean distance metric. Then if you have one particle in two blobs separated by 1 unit, it’s 1 unit distant. If you have two, it’s now separated by 1 unit along each of two axes, so it’s sqrt(2) distant. For N particles in two blobs, the blobs are sqrt(N) distant.
I’ve got the same questions as Psy-Kosh and DavidAgain. Why?
In light of this, consider the cosmologist’s claim that the total energy of the universe- rest-mass plus kinetic plus all the fields, especially gravitational, could very well turn out to be zero. Then your entropic formulation here could suggest a plausible answer to “Why is there something rather than nothing?” and “Why did the entropy of the universe used to be so low?” If, initially there was nothing, it takes no information to specify the universe’s state. Minimum entropy. The spontaneous introduction of particles (with no net energy change) represents an increase in entropy. The process by which that initial state would rise in entropy is still ongoing, just as a hot object takes finite time to reach equilibrium with it’s surroundings. In the case of a star that process can take trillions of years.
http://www.nytimes.com/2010/02/16/science/16quark.html?pagewanted=all seems to be an article about violating parity, which I’m guessing is what you’re talking about here? If so, it’s nice finally having a context for that article :)
Parity is just one component of CPT symmetry. If you just interchange left and right, physics is almost the same, but not quite. That article is about measuring that asymmetry. If, however, all three components are interchanged, then, as far as we know, the laws of physics are exactly the same, which is what is used to prove the second law of thermodynamics.
I’ve on my second reading of the Quantum Physics Sequence, and this struck me the first time as well, so now I’ve got to ask.
“The system at left is highly entangled—it’s got a joint distribution that looks something like, ‘There’s two particles, and either they’re both over here, or they’re both over there.’”
Isn’t this wrong, given the diagram? Wouldn’t a description of this diagram be, “There are two particles, one over here and one over there?” Why wouldn’t the diagram fold along the diagonal like in the “No Individual Particles” post? Wouldn’t a diagram with a blob in the top-right and a blob in the lower-left better match the description given?
Indeed, if the two axes are the coordinates of the two particles, then one blob should be in the lower left and the other in the upper right. Seems Eliezer made a mistake with this diagram.
Eliezer, thank you for your posts. I’m new to this site—not to mention to QM—and I’ve been reading this series with much interest, albeit with fluctuating success.
I’ve been concentrating on the Intuitive Explanation index, re-reading the posts and comments several times over, but I’m pretty sure I’m still missing some important aspect. This is what I’m getting so far. I would love it if somebody more knowledgeable could point out where exactly my understanding went astray.
I get that any particle, such as an electron, is actually a (part of a) wave moving over some field. This wave, or wavefunction, has values all over the place: it is a complex-valued, continuous and differentiable distribution over 3 dimensions (plus time.)
Because of the constraints implicit in the wave mechanics, these 3 dimensions can be taken to be the position space or equivalently the momentum space. You stated in some other post that you prefer the position space, as it makes the “locality principle” of the universe more readily apparent. Ok.
This is already suggesting that a “particle” does not have a definite position, nor a definite momentum, only a definite, complex-valued distribution over both, that’s constantly changing over time.
So for example, at position (x, y, z) and time (t), there is a complex amplitude (r, φ) on the quantum field for electrons. It’s a distribution because it is zero at any single point and only the integral has non-zero values. (By the way, how many quantum fields are there?)
The distribution, which comprises all existing electrons in the universe, is moving through space with some kind of wave dynamics, so that the way it evolves over time is determined by its very shape and motion (its derivatives.) Just like an ocean or sound wave, except with complex values—and I bet complex math :-) All right so far.
So it can happen that two particles of the same kind (two wavelets on the same field) manage to evolve into exactly opposite distributions and thus cancel each other out. No big deal, this happens all the time with fluid or sound waves too.
As far as I can see, this should explain “entangled” particles, as they would be wavelets originating from the same wave, so that their sub-distributions are closely related to each other. If you measure some quantity on one of them, then you know the quantity of the other, because it’s closely related, such as the opposite.
As far as the half-silvered mirrors go, if you can detect one path an electron or photon takes, you cannot detect any other path it took (being a wave it took all possible paths) because on the other paths the wave has a different complex phase. Except that if you direct them back on the same path, they can cancel each other out. This does not usually happen with two generic particles (wavelets) created from different sources, because they would have different distributions (would not be coherent.)
This is also true of complex waveforms, such as humans or cats or tables, except that, out of all their Feynman paths, only the tiniest slice does not cancel out, and that’s why we don’t see tables moving around.
What I don’t get is the need to call the collective distribution (or wave, or wavefunction) of all the electrons in the universe a “configuration” and posit that it has itself an amplitude (or amplitude distribution) over the infinitely larger space of all possible configurations, something the mind has a hard time grasping. I’m not even sure this is exactly what is being suggested, but I’m afraid it is so, because of the many-world interpretation that comes out of it.
I’m sure I’m missing something very important in all this, or I got different concepts mixed together. Exactly which one of the half-silvered mirror experiments or other posts explains the need for such a complication? Which parts of my understanding above are wrong?
Thank you for this article.
Many worlds seem not so much an interpretation anymore. They are really there as different non-interacting blobs!