Using vector fields to visualise preferences and make them consistent
This post was written for Convergence Analysis by Michael Aird, based on ideas from Justin Shovelain and with ongoing guidance from him. Throughout the post, “I” will refer to Michael, while “we” will refer to Michael and Justin or to Convergence as an organisation.
Epistemic status: High confidence in the core ideas on an abstract level. Claims about the usefulness of those ideas, their practical implications, and how best to concretely/mathematically implement them are more speculative; one goal in writing this post is to receive feedback on those things. I’m quite new to many of the concepts covered in this post, but Justin is more familiar with them.
Overview
This post outlines:
What vector fields are
How they can be used to visualise preferences
How utility functions can be generated from “preference vector fields” (PVFs)
How PVFs can be extrapolated from limited data on preferences
How to visualise inconsistent preferences (as “curl”)
A rough idea for how to “remove curl” to generate consistent utility functions
Possible areas for future research
We expect this to provide useful tools and insights for various purposes, most notably AI alignment, existential risk strategy, and rationality.
This post is structured modularly; different sections may be of interest to different readers, and should be useful in isolation from the rest of the post. The post also includes links to articles and videos introducing relevant concepts, to make the post accessible to readers without relevant technical backgrounds.
Vector fields and preferences
A vector represents both magnitude and direction; for example, velocity is a vector that represents not just the speed at which one is travelling but also the direction of travel. A vector field essentially associates a vector to each point in a region of space. For example, the following image (source) shows the strength (represented by arrow lengths) and direction of the magnetic field at various points around a bar magnet:
Figure 1.
Another common usage of vector fields is to represent the direction in which fluid would flow, for example the downhill flow of water on uneven terrain (this short video shows and discusses that visualisation).
We believe that vector fields over “state spaces” (possible states of the world, represented by positions along each dimension) can be a useful tool for analysis and communication of various issues (e.g., existential risk strategy, AI alignment). In particular, we’re interested in the idea of representing preferences as “preference vector fields” (PVFs), in which, at each point in the state space, a vector represents which direction in the state space an agent would prefer to move from there, and how intense that preference is.[1] (For the purposes of this post, “agent” could mean an AI, a human, a community, humanity as a whole, etc.)
To illustrate this, the following PVF shows a hypothetical agent’s preferences over a state space in which the only dimensions of interest are wealth and security.[2][3]
Figure 2.
The fact that (at least over the domain shown here) the arrows always point at least slightly upwards and to the right shows that the agent prefers more wealth and security to less, regardless of the current level of those variables. The fact that the arrows are longest near the x axis shows that preferences are most intense when security is low. The fact that the arrows become gradually more horizontal as we move up the y axis shows that, as security increases, the agent comes to care more about wealth relative to security.
Not only preferences
In a very similar way, vector fields can be used to represent things other than preferences. For example, we might suspect that for many agents (e.g., most/all humans), preferences do not perfectly match what would actually make the agent happier (e.g., because of the agent being mistaken about something, or having separate systems for reward vs motivation). In this case, we could create a vector field to represent the agent’s preferences (represented by the blue arrows below), and another to represent what changes from any given point would increase the agent’s happiness (represented by the green arrows).
Figure 3.
This method of layering vector fields representing different things can be used as one tool in analysing potential clashes between different things (e.g., between an agent’s preferences and what would actually make the agent happy, or between an agent’s beliefs about what changes would be likely at each state and what changes would actually be likely at each state).
For example, the above graph indicates that, as wealth and/or security increases (i.e., as we move across the x axis and/or up the y axis), there is an increasing gap between the agent’s preferences and what would make the agent happy. In particular, security becomes increasingly more important than wealth for the agent’s happiness, but this is not reflected in the agent’s preferences.
(Note that, while it does make sense to compare the direction in which arrows from two different vector fields point, I haven’t yet thought much about whether it makes sense to compare the lengths Grapher shows for their arrows. It seems like this is mathematically the same as the common problem of trying to compare utility functions across different agents, or preferences across different voters. But here the functions represent different things within the same agent, which may make a difference.)
Gradients and utility functions
When a vector field has no “curl” (see the section “Curl and inconsistent preferences” below), the vector field can be thought of as the gradient of a scalar field.[4] (A scalar field is similar to a vector field, except that it associates a scalar with each point in a region of space, and scalars have only magnitude, rather than magnitude and direction.) Essentially, this means that the arrows of the vector field can be thought of as pointing “uphill”, away from low points and towards high points of the associated scalar function. If the vector field represents preferences, higher points of the scalar function would be where preferences are more satisfied, and lower points are where it is less satisfied; thus, the scalar function can be thought of as the agent’s utility function.[5] (The same basic method is often used in physics, in which context the scalar function typically represents scalar potential.)
Below is one visualisation of the scalar field representing the utility function of the agent from the previous example (based on its preferences, not on what would make it “happy”), as well as the related vector field. Colours towards the red end of the spectrum represent higher values of the scalar field. It can be seen that the arrows of the vector field point away from blue areas and towards red areas, representing the agent’s preference for “climbing uphill” on its utility function.
Figure 4.
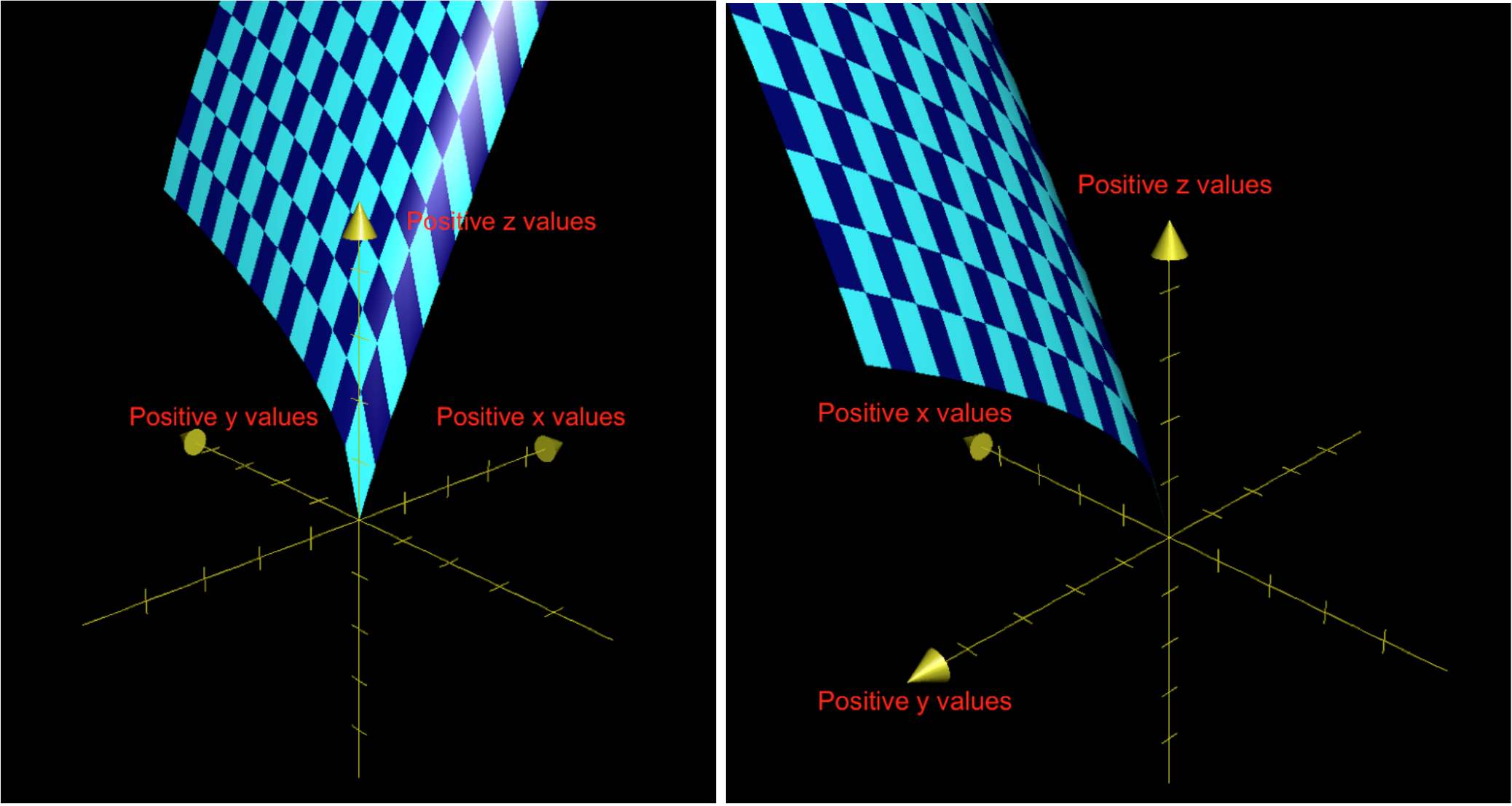
The scalar field can also be represented in three dimensions, as values on the z dimension, which are in turn a function of values on the x and y dimensions. This is shown below (from two angles), for the same agent. (These graphs are a little hard to interpret from still images on a 2D screen, at least with this function; such graphs can be easier to interpret when one is able to rotate the angle of view.)
Figures 5a and 5b.
Method
This video provides one clear explanation of the actual method for determining the scalar function that a curl-free vector field can be thought of as the gradient of (though the video is focused on cases of 3D vector fields). That video describes this as finding the “potential”; as noted earlier, when the vector field represents preferences, the utility function can be thought of as analogous to the “potential” in other cases.
Personally, as a quick method of finding the scalar function associated with a 2D vector field, I used the following algorithm, from the first answer on this page:
DSolve[{D[f[x, y], x] == [X COMPONENT OF THE VECTOR FIELD], D[f[x, y], y] == [Y COMPONENT OF THE VECTOR FIELD]}, f[x, y], {x, y}]
I input the algorithm into a Wolfram Cloud notebook, which seems to be free to use as long as you create an account. (As noted in the answer on the linked page, this algorithm will come back with no solution if the vector field has curl. This makes sense, because this general approach cannot be used in this way if a field has curl; this is explained in the section “Curl and inconsistent preferences” below.) Finally, I double-checked that the function was a valid solution by using this calculator to find its gradient, which should then be the same as the original vector field.
Extrapolating PVFs (and utility functions) from specific preference data
In reality, one rarely knows an agent’s actual utility function or their full PVF. Instead, one is likely to only have data on the agent’s (apparent) preferences at particular points in state space; for example, the extent to which they wanted more wealth and more security when they had $10,000 of savings and a “4/5” level of security.
One can imagine extrapolating a full preference vector field (PVF) from that data. We do not know of a precise method for actually doing this (we plan to do more research and thought regarding that in future). However, conceptually speaking, it seems the process would be analogous to fitting a regression line to observed data points, and, like that process, would require striking a balance between maximising fit with the data and avoiding overfitting.
For an example (based very loosely on Figure 3 in this article), suppose that I know that Alice prefers car A to Car B, Car B to Car C, Car C to Car D, and Car D to Car A (i.e., to Alice, A>B>C>D>A).[6] I also know the weight (in thousands of pounds) and perceived “sportiness” (as rated by consumers) of the four cars, and am willing to make the simplifying assumption that these are the only factors that influenced Alice’s preferences. I could then create a plane with weight on the x axis and sportiness on the y axis, show the position of the four cars in this space, and represent Alice’s preferences with arrows pointing from each car towards the car Alice would prefer to that one, as shown below:[7]
Figure 6.
I could then infer a PVF that (1) approximately captures Alice’s known preferences, and (2) suggests what preferences Alice would have at any other point in the plane (rather than just at the four points I have data for). In this case, one seemingly plausible PVF is shown below, with the length of each blue arrow representing the strength of Alice’s preferences at the associated point. (This PVF still shows Alice’s known preferences, but this is just for ease of comparison; those known preferences are not actually part of the PVF itself.)
Figure 7.
This PVF allows us to make predictions about what Alice’s preferences would be even in situations we do not have any empirical data about. For example, this PVF suggests that if Alice had the hypothetical car E (with a weight of ~2000 pounds and sportiness of ~55), she would prefer a car that was heavier and was higher for sportiness. In contrast, the PVF also suggests that, if she had the hypothetical car F (with a weight of ~6000 pounds and sportiness of ~55), she would prefer a car that was heavier and was rated lower for sportiness.
Of course, these predictions are not necessarily accurate. One could likely create many other PVFs that also “appear” to roughly fit Alice’s known preferences, and these could lead to different predictions. This highlights why we wish to find a more precise/“rigorous” method to better accomplish the goal I have conceptually gestured at here.
It’s also worth noting that one could extrapolate an agent’s utility function from limited preference data by first using the method gestured at here and then using the method covered in the previous section. That is, one could gather some data on an agent’s (apparent) preferences, extrapolate a PVF that “fits” that data, and then calculate what (set of) scalar function(s) that vector field is the gradient of. That scalar function would be the agent’s extrapolated utility function.
However, as noted earlier, this method only works if the PVF has no “curl”, so it would not work in the case of Alice’s preferences about cars. I will now discuss what I mean by “curl”, what implications curl has, and a rough idea for “removing” it.
Curl and inconsistent preferences
In the example above, to Alice, A>B>C>D>A. This is a case of intransitivity, or, less formally, circular or inconsistent preferences. This is typically seen as irrational, and as opening agents up to issues such as being “money pumped”. It seems that Alice would be willing to just keep paying us to let her trade in one car for the one she preferred to that one, and do this endlessly—going around and around in a circle, yet feeling that her preferences are being continually satisfied.
So another pair of reasons why representing preferences as vector fields is helpful is that doing so allows inconsistencies in preferences:
to be directly seen (if they are sufficiently extreme)
to be calculated as the vector field’s curl
This video introduces the concept of curl. Returning to the visualisation of vector fields as representing the direction in which water would flow over a certain domain, curl represents the speed and direction an object would spin if placed in the water. For example, if there is a strong clockwise curl at a certain point, a stick placed there would rotate clockwise; if there is no curl at a point, a stick placed there would not rotate (though it still may move in some direction, as represented by the vector field itself).
Note that the concepts of curl and inconsistency will also apply in less extreme cases (i.e., where an agent’s preferences do not only “chase each other around in circles”).
As noted earlier, when a vector field has curl, one cannot find its gradient. In our context, this seems logical; if an agent’s preferences are inconsistent, it seems that the agent cannot have a true utility function, and that we can’t assign any meaningful “height” to any point in the 2D state space. Consider again the example of Alice’s preferences for cars; if we were to interpret meeting her preferences as moving “uphill” on a utility function, she could keep arriving back at the same points in the state space and yet be at different “heights”, which doesn’t seem to make sense.
Removing curl to create consistent utility functions
It seems that agents frequently have intransitive preferences, and thus that their PVFs will often have some curl. It would therefore be very useful to have a method for “removing curl” from a PVF, to translate an intransitive set of preferences into a transitive set of preferences, while making a minimum of changes. This new, consistent PVF would also then allow for the generation of a corresponding utility function for the agent.[8]
We believe that this process should be possible. We also believe that, if developed and confirmed to make sense, it could be useful for various aspects of AI alignment (among other things). In particular, it could help in:
extrapolation of a consistent “core” (and corresponding utility function) from inconsistent human preferences (which could then inform an AI’s decisions)
adjustment of an AI’s inconsistent preferences (either by engineers or by the AI itself), with a minimum of changes being made
We have not yet implemented this process for removing curl. But we believe that the Helmholtz theorem should work, at least for PVFs in 3 or fewer dimensions (and we believe that a higher dimensional generalization probably exists). The Helmholtz theorem:
states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field; this is known as the Helmholtz decomposition or Helmholtz representation. (Wikipedia)
This irrotational (curl-free) vector field would then be the consistent projection (in a CEV-like way) of the agent’s preferences (from which the agent’s utility function could also be generated, in the manner discussed earlier).
Uncertainties and areas for further research
The following are some areas we are particularly interested in getting comments/feedback on, seeing others explore, or exploring ourselves in future work:
Are there any flaws or misleading elements in the above analysis? (As noted earlier, this is essentially just an initial exploration of some tools/concepts.)
To what extent do the methods used and claims made in this post generalise to higher-dimensional spaces (e.g., when we wish to represent preferences over more than two factors at the same time)? To what extent do they generalise to graphs of states that don’t correspond to any normal geometry?
Is there an existing, rigorous/precise method for extrapolating a PVF from a limited number of known preferences (or more generally, extrapolating a vector field from a limited number of known vectors)? If not, can a satisfactorily rigorous/precise method be developed?
Are there meaningful and relevant differences between the concepts of curl in vector fields and of intransitivity, inconsistency, irrationality, and incoherence in preferences? If so, how does that change the above analysis?
Is it possible to “remove curl” in the way we want, in the sort of situations we’re interested in (in particular, not only in three dimensions)? If so, how, specifically?
What other implications do the above ideas have? E.g., for rationality more generally, or for how to interpret and implement preference utilitarianism. (Above, I mostly just introduced the ideas, and hinted at a handful of implications.)
What other uses could these “tools” be put to?
- ↩︎
- ↩︎
Of course, there are often far more than two key factors influencing our preferences. In such cases, a vector field over more dimensions can be used instead (see here for an introduction to 3D vector fields). I focus in this post on 2D vector fields, simply because those are easier to discuss and visualise. We expect many of the ideas and implications covered in this post will be similar in higher dimensional vector fields, but we aren’t yet certain about that, and intend to more carefully consider it later.
- ↩︎
For both this example and most others shown, the precise equations used were chosen quite arbitrarily, basically by trying equations semi-randomly until I found one that roughly matched the sort of shape I wanted. For those interested, I have screenshots of all equations used, in their order of appearance in this post, here. To create the visuals in this post, I entered these equations into Grapher (for those interested in trying to do similar things themselves, I found this guide useful). I discuss below, in the section “Extrapolating PVFs (and utility functions) from specific preference data”, the issue of how to actually generate realistic/accurate PVFs in the first place.
- ↩︎
It’s possible that here I’m conflating the concepts of conservative, irrotational, and curl-free vector fields in a way that doesn’t make sense. If any readers believe this is the case, and especially if they believe this issue changes the core ideas and implications raised in this post, I would appreciate them commenting or messaging me.
- ↩︎
Technically, the vector field is the gradient of a class of functions, with the functions differing only in their constant term. This is because gradient only relates to differences in height (or roughly analogous ideas, in higher-dimensional cases), not to absolute heights. One can imagine raising or lowering the entire scalar function by the same constant without affecting the gradient between points. (I show in this document examples of what this would look like, while in this post itself I keep all constants at 0.) Thus, in one sense, a PVF does not fully specify the associated utility function representation, but the constant can be ignored anyway (as utility functions are unique up to positive affine transformations).
- ↩︎
I have purposefully chosen a set of circular (or “intransitive”) preferences, as the next session will use this example in discussing the problem of circularity and how to deal with it.
- ↩︎
Note that, in this example, I am not assuming any knowledge about the strength of Alice’s preferences, only about their direction. As such, the length of the arrows representing Alice’s known preferences has no particular meaning.
- ↩︎
In conversation with Justin, Linda Linsefors mentioned having had a somewhat similar idea independently.
- 2020 AI Alignment Literature Review and Charity Comparison by (EA Forum; Dec 21, 2020, 3:25 PM; 155 points)
- 2020 AI Alignment Literature Review and Charity Comparison by (Dec 21, 2020, 3:27 PM; 142 points)
- Improving the future by influencing actors’ benevolence, intelligence, and power by (EA Forum; Jul 20, 2020, 10:00 AM; 77 points)
- CEEALAR Fundraiser 9: Concrete outputs after 29 months by (EA Forum; Nov 27, 2020, 2:48 PM; 69 points)
- Resolving von Neumann-Morgenstern Inconsistent Preferences by (Oct 22, 2024, 11:45 AM; 38 points)
- Feature suggestion: Could we get notifications when someone links to our posts? by (Mar 5, 2020, 8:06 AM; 36 points)
- Turning Some Inconsistent Preferences into Consistent Ones by (Jul 18, 2022, 6:40 PM; 23 points)
- Value uncertainty by (Jan 29, 2020, 8:16 PM; 20 points)
- How Money Fails to Track Value by (Apr 2, 2022, 12:32 PM; 17 points)
- [AN #89]: A unifying formalism for preference learning algorithms by (Mar 4, 2020, 6:20 PM; 16 points)
- 's comment on Is “VNM-agent” one of several options, for what minds can grow up into? by (Dec 30, 2024, 12:34 PM; 16 points)
- 's comment on Why Not Just… Build Weak AI Tools For AI Alignment Research? by (Mar 5, 2023, 10:30 AM; 13 points)
- 's comment on Inferring utility functions from locally non-transitive preferences by (Feb 12, 2022, 10:43 AM; 9 points)
- 's comment on Formal Philosophy and Alignment Possible Projects by (Jul 2, 2022, 1:17 PM; 3 points)

I think you can extend this idea to graphs.
Beat me to it. Yeah, it seems that Hodge decomposition of graph flows is the right tool here.
The papers make it sound a bit scary, so I’ll try to explain it simpler: imagine a complete graph on N vertices, two of which are marked A and B, and a flow F on that graph, which is nonzero on the edge from A to B and zero everywhere else. We can write it like this, where ∗ means “any vertex except A or B”:
Then F can be written as the sum of these two flows C and G:
The reason for this choice is that C is a “cyclic” flow, which means there are no sources or sinks—the net contribution of each vertex is 0. And G is a “gradient” flow, which means there’s a function P (“potential”) such that G(X,Y) = P(X)-P(Y) for any two vertices X and Y:
This construction is easy to generalize: since every flow on our graph is a linear combination of flows like F that are nonzero on only one edge, and the conditions on cyclic and gradient flows are also linear, we can rewrite any flow as a sum of cyclic and gradient flows and find the potential function up to a constant. For example, if we start with a cyclic flow, then G will be everywhere zero and P will be constant.
A more complex version of this also works for non-complete graphs. For any flow on any graph, the decomposition into cyclic and gradient flows is unique, and the potential function is unique up to a constant per each connected component of the graph.
In principle, this idea lets us infer complete and consistent preferences from incomplete and/or inconsistent preferences. Apparently it has been used in practical problems, like the Netflix prize. I’d love to hear from people who have experience with it.
You might find this paper interesting. It does a similar decomposition with the dynamics of differentiable games (where the ‘preferences’ for how to change your strategy may not be the gradient of any function)
https://arxiv.org/abs/1802.05642
“The key result is to decompose the second-order dynamics into two components. The first is related to potential games, which reduce to gradient descent on an implicit function; the second relates to Hamiltonian games, a new class of games that obey a conservation law, akin to conservation laws in classical mechanical systems.”
I believe this is precisely the wrong thing to be trying to do. We should be trying to philosophically understand how intransitive preferences can be (collectively) rational, not trying to remove them because they’re individually irrational.
(I’m going to pose the rest of this comment in terms of “what rules should an effectively-omnipotent super-AI operate under”. That’s not because I think that such a singleton AI is likely to exist in the foreseeable future; but rather, because I think it’s a useful rhetorical device and/or intuition pump for thinking about morality.)
Once you’ve reduced everything down to a single utility function, and you’ve created an agent or force substantially more powerful than yourself who’s seeking to optimize that utility function, it’s all downhill from there. Or uphill, whatever; the point is, you no longer get to decide on outcomes. Reducing morality to one dimension makes it boring at best; and, if Goodhart has anything to say about it, ultimately even immoral.
Luckily, “curl” (intransitive preference order) isn’t just a matter of failures of individual rationality. Condorcet cycles, Arrow’s theorem, the Gibbard-Satterthwaite theorem; all of these deal with the fact that collective preferences can be intransitive even when the individual preferences that make them up are all transitive.
Imagine a “democratic referee” AI (or god, or whatever) that operated under roughly the following “3 laws”:
0. In comparing two world-states, consider the preferences of all “people” which exist in either, for some clear and reasonable definition of “people” which I’ll leave unspecified.
1. If a world-state is Pareto dominated, act to move towards the Pareto frontier.
2. If an agent or agents are seeking to change from one world-state A to another B, and neither of the two pareto dominates, then thwart that change iff a majority prefers the status quo A over B AND there is no third world-state C such that a majority prefers B over C and a majority prefers C over A.
3. Accumulate and preserve power, insofar as it is compatible with laws 1 and 2.
An entity which followed these laws would be, in practice, far “humbler” than one which had a utility function over world-states. For instance, if there were a tyrant hogging all the resources that they could reasonably get any enjoyment whatsoever out of, the “referee” would allow that inequality to continue; though it wouldn’t allow it to be instituted in the first place. Also, this “referee” would not just allow Omelas to continue to exist; it would positively protect its existence for as long as “those who walk away” were a minority.
So I’m not offering this hypothetical “referee” as my actual moral ideal. But I do think that moral orderings should be weak orderings over world states, not full utility functions. I’d call this “humble morality”; and, while as I said above I don’t actually guess that singleton AIs are likely, I do think that if I were worried about singleton AIs I’d want one that was “humble” in this sense.
Furthermore, I think that respecting the kind of cyclical preferences that come from collective preference aggregation is useful in thinking about morality. And, part of my guess that “singleton AIs are unlikely” comes from thinking that maintaining/enforcing perfectly coherent aggregated preferences over a complex system of parts is actually a harder (and perhaps impossible) problem than AGI.
(My own view, not Convergence’s, as with most/all of my comments)
I think that’s quite an interesting perspective (and thanks for sharing it!). I think I’m new enough to this topic, and it’s complicated enough, that I personally should sort-of remain agnostic for now on whether it’s better to a) try to find a “consistent version” of a person’s actual, intransitive preferences, or b) just accept those intransitive preferences and try to fulfil them as best we can.
As an example of my agnosticism on a very similar question, in another post I published the day after this one, I wrote:
Also, somewhat separately from the broader question of “fixing” vs “accepting” intransitivity, I find your idea for a “humble morality” or “democratic referee” singleton quite interesting. At first glance, it seems plausible as a way to sort-of satisfice in an acceptable way—guaranteeing a fairly high chance of an acceptably good outcome, even if perhaps at the cost of not getting the very best outcomes and letting some value be lost. I’d be interested in seeing a top level post fleshing that idea out further (if there isn’t one already?), and/or some comments seeing if they can tear the idea apart :D
Parts of your comment also reminded me of Rohin Shah’s post on AI safety without goal directed behaviour (and the preceding posts), in which he says, e.g.:
One small nit-pick/question, though: you write “Reducing morality to one dimension makes it boring at best; and, if Goodhart has anything to say about it, ultimately even immoral.” I don’t see why creating a “consistent version” of someone’s preferences and extracting a utility function from that would be reducing morality to one dimension. The utility function could still reflect a lot of the complexity and fragility of values (caring about many different things, caring about interactions between things, having diminishing returns or “too much of a good thing”, etc.), even if it does shave off some/a lot of that complexity for the sake of consistency.
I guess we could say that the whole utility function is the “one dimension”, but that’d seem misleading to me. That’s because it seems like the usual reason given for worrying about something like a “one-dimensional morality” is that it won’t reflect that we value multiple things in complicated ways, whereas the whole utility function can reflect that (at least in part, even if it doesn’t fully capture our original, intransitive values).
Am I misunderstanding what you meant there?
Yes, the utility function is the “one dimension”. Of course, it can be as complicated as you’d like, taking into account multiple aspects of reality. But ultimately, it has to give a weight to those aspects; “this 5-year-old’s life is worth exactly XX.XXX times more/less than this 80-year-olds’ life” or whatever. It is a map from some complicated (effectively infinite-dimensional) Omega to a simple one-dimensional utility.
I think you do need preference aggregation, not just conflict resolution. For example, if the AI finds $100 on the ground, should it give the money to Alice or Bob? Either would be a Pareto improvement over the current state. To decide, it needs weighting coefficients for different people’s utilities—which direction vector to take when moving toward the Pareto frontier. That’s the same information as having a joint utility function. And that utility function could end up determining most of the future, if the universe has lots of stuff that the AI can acquire and give to humans, compared to stuff that humans can acquire by themselves.
Good point. Here’s the raw beginnings of a response:
The idea here would be to resolve such questions “democratically” in some sense. I’m intentionally leaving unspecified what I mean by that because I don’t want to give the impression that I think I could ever tie up all the loose ends with this proposal. In other words, this is a toy example to suggest that there’s useful space to explore in between “fully utilitarian agents” and “non-agents”, that agents with weakly-ordered and/or intransitive preferences may in some senses be superior to fully-utilitarian ones.
I realize that “democratic” answers to the issue you raise will tend to be susceptible to the “Omelas problem” (a majority that gets small benefits by imposing large costs on a minority) and/or the repugnant conclusion (“cram the world with people until barely-over-half of their lives are barely-better-than-death”). Thus, I do not think that “majority rules” should actually be a foundational principle. But I do think that when you encounter intransitivity in collective preferences, it may in some cases be better to live with that than to try to subtract it out by converting everything into comparable-and-summable utility functions.
Sometime ago I made this argument to Said Achmiz:
With that in mind, can you try spelling out in what sense an inconsistent system could be better?
Consistency is the opposite of humility. Instead of saying “sometimes, I don’t and can’t know”, it says “I will definitively answer any question (of the correct form)”.
Let’s assume that there is some consistent utility function that we’re using as a basis for comparison. This could be the “correct” utility function (eg, God’s); it could be a given individual’s extrapolated consistent utility; or it could be some well-defined function of many people’s utility.
So, given that we’ve assumed that this function exists, obviously if there’s a quasi-omnipotent agent rationally maximizing it, it will be maximized. This outcome will be at least as good as if the agent is “humble”, with a weakly-ordered objective function; and, in many cases, it will be better. So, you’re right, under this metric, the best utility function is equal-or-better to any humble objective.
But if you get the utility function wrong, it could be much worse than a humble objective. For instance, consider adding some small amount of Gaussian noise to the utility. The probability that the “optimized” outcome will have a utility arbitrarily close to the lower bound could, depending on various things, be arbitrarily high; while I think you can argue that a “humble” deus ex machina, by allowing other agents to have more power to choose between world-states over which the machina has no strict preference, would be less likely to end up in such an arbitrarily bad “Goodhart” outcome.
This response is a bit sketchy, but does it answer your question?
It makes sense to value other agents having power, but are you sure that value can’t be encoded consistently?
In case you weren’t aware, this is no longer true if the state space has “holes” (formally: if its first cohomology group is non-zero). For example, if the state space is the Euclidean plane without the origin, you can have a vector field on that space which has no curl but isn’t conservative (and thus is not the gradient of any utility function).
Why this might be relevant:
1. Maybe state spaces with holes actually occur, in which case removing the curl of the PVF wouldn’t always be sufficient to get a utility function
2. The fact that zero curl only captures the concept of transitivity for certain state spaces could be a hint that conservative vector fields are a better concept to think about here than irrotational ones (even if it turns out that we only care about simply connected state spaces in practice)
EDIT: an example of an irrotational 2D vector field which is not conservative is v(x,y)=(−yx2+y2,xx2+y2) defined for (x,y)∈R2∖{0}
Regarding higher-dimensional space. For a Riemannian manifold M of any dimension, and a smooth vector field V, we can pose the problem: find smooth U:M→R that minimizes ∫M||∂U(x)−V(x)||2μ(dx), where μ is the canonical measure on M induced by the metric. If either M is compact or we impose appropriate boundary conditions on U and V, then I’m pretty sure this equivalent to solving the elliptic differential equation ΔU=∂⋅V. Here, the Laplacian and ∂V are defined using the Levi-Civita connection. If M is connected then, under these conditions, the equation has a unique solution up to an additive constant.
Very neat post.
Intransitive preferences can be found from a series of binary choices, but if you force a ranking among the full set, you won’t have intransitive preferences (i.e., you can write out a gradient). This also means the elicitation procedure affects your inferences about the vectors. It would seem that circular preferences “fit,” but really they could just be fitting the (preferences | elicitation method) rather than “unconditional” (“core” + “irrationality,” whatever irrationality means) preferences. Preferences are also not independent of “irrelevant” alternatives as perceived attribute levels are evaluated contextually (that’s necessarily irrational?).
One implication I see here is that 0 vectors are points with no inclination to switch or having “no desire.” These would be useful model falsification points (e.g., Figure 7 implies that people don’t care about sportiness at all conditional on weight being “right”). But they would also only seem to correspond to ideal points or “ideal configuration” points. Without data on what the agent wants and only on what they are being offered (“I want a sporty car, but not too sporty; Car A is closest, but still not quite right, too bad”), you’ll be fitting the wrong hill to run up.
One problem with getting peoples’ entire ranking at once is that we’re cognitively incapable of ranking all states of the universe, so some approximation has to be used.
Your point about the elicitation method is interesting. In some sense, the problem is utterly inescapable, because “what do you think about A?” is literally a different elicitation than “what do you think about B?”, prompting the listener to think of different rating criteria.
Yeah, I think the points about elicitation methods and about the influence of irrelevant alternatives are important, and I don’t really have a great answer/solution. But I can say that this sounds quite related to some problems Stuart Armstrong has posted about in quite a few places, and that he seems to have some useful ideas for. E.g. in the “”Reasonable” situations” section of this post.
Charlie Steiner, right, it’s not doable for, say, all products on (or could be on) the market, but it is certainly doable among the products in a person’s consideration set. If we posit that they would make a choice among 4, then eliciting binary preferences might—but also might not—faithfully reflect how preferences look in the 4 set. So to MichaelA’s point, if preferences are context-dependent, then you need to identify appropriate contexts, or reasonable situations.
Context-dependent preferences present a big problem because “true” context-less preferences...maybe don’t exist. At the very least, we can make sure we’re eliciting preferences in an ecologically-valid way.
Binary choices are useful, but when they lead to inconsistencies, one should wonder whether it’s because preferences are inconsistent or whether it’s an elicitation thing. If people really would choose between A and B and not consider C or D, then ranking A and B is the relevant question. If people would consider A, B, C, and D (or at least pick between A and B in the context of C and D) then ranking all four (or at least ranking A and B in the context of C and D) is the relevant question.
Perhaps the missing variable is cost.
Interesting thought for me: one thing this implies is that *not* collapsing goodharting might be a social strategy for more coordination schelling points
How so? I don’t follow your comment’s meaning.
I want some latitude to commit to things to that are only partially entangled with my values since that lets me coordinate with a broader range of people. If there is mutual knowledge about this necessity then the coordination is also more metastable.
Interesting. I’m, naturally, interested in the way we might make sense of this in light of valence. For example, can we think of valence as determining the magnitude of a vector (including the ability to flip the vector via a negative magnitude) and direction as about pointing to a place in idea/category space? Maybe this will prove a useful simplification over whatever it is that the brain actually does with valence to help it make decisions to make reasoning about how decisions are made easier and more tractable for aligning AI to.
Here’s the fundamental, concrete problem: if you figure out “the best state of the universe,” do you just make the universe be in that state for ever and ever? No, that sounds really, really boring.
Which is to say, it’s possible for a scheme like this to not even include good results in its hypothesis space.
Also, yeah, figure out how Helmholtz decomposition works. It’s useful.
You can work around this by making your “state space” descriptions of sequences of states. And defining preferences between these sequences.
Sure. But same as DanielV’s point about elimiating circularity by just asking for the complete preference ordering, we are limited by what humans can think about.
Humans have to think in terms of high-level descriptions of approximately constant size, no matter the spatiotemporal scale. We literally cannot elicit preferences over universe-histories, much as we’d like to.
What we can do, maybe, is elicit some opinions on these “high-level descriptions of approximately constant size,” at many different spatiotemporal scales: ranging from general opinions on how the universe should go to what could improve the decor of your room today. Stitching these together into a utility function over universe histories is pretty tricky, but I think there might be some illuminating simplifications we could think about.
I think I agree strongly with the spirit of that, but would frame it differently. I’d say that this approach could fail to consider extremely important dimensions over which the agent has value. Indeed, all examples in the post very likely do so. Alice probably also cares about other things, such as safety, cost, fuel efficiency, etc. So it could be that the ideal car would have a sportiness of 50 and a weight of 6 (or whatever), but also that the vast majority of such cars would be disliked, because the ideal car has that as well as some very specific scores for various other dimensions.
So I think that the problem is really that this approach could very easily fail to sufficiently specify the states, so that, even if the good result is included in its hypothesis space, achieving “that good result” is actually still a quite wide target and many ways of doing so would be bad.
This seems very related to the idea that value is fragile.
As for the specific issue you (Charlie Steiner, not FactorialCode) raise, I think there are multiple possible workarounds. One is what FactorialCode suggests. Another would be to add another dimension to capture “similarity to what has come before and will come after”, or “variety compared to what the agent is used to”, or “amount of change within this state”, or something like that.
Note that, as stated above, any dimensions that aren’t specified within the state space are free to vary, with this still counting as the “same state”. So if the agent wants “variety” for its own sake, and is fine with this being variety along dimensions it doesn’t otherwise care about, that could be fairly easy to accommodate. It would get trickier if the agent wants variety along dimensions it does otherwise care about, but it still seems some workarounds could work.
But this is of course just patching one specific issue, and I still think that the fact we could easily neglect important dimensions matters a lot. But I think that’s important for any efforts towards alignment or capturing preferences.
As mentioned, I did think of this of this model before, and I also disagree with Justin/Convergence on how to use it.
Lets say that the underlying space for the vector field is the state of the world. Should we really remove curl? I’d say no. It is completely valid to want to move along some particular path, even a circle, or more likely, a spiral.
Alternatively, lets say that the underlying space for the vector field is world histories. Now we should remove curl, becasue any circular preference in this space is inconsistent. But what even is the vector field in this picture?
***
My reason for considering values as a vector is becasue that is sort of how it feels to me on the inside. I have noticed that my own values are very different depending on my current mood and situation.
When I’m sand/depressed, I become a selfish hedonist. All I care about is for me to be happy again.
When I’m happy I have more complex and more altruistic values. I care about truth and the well-being of others.
It’s like these wants are not tracking my global values at all, but just pointing out a direction in which I want to move. I doubt that I even have global values, because that would be very complicated, and also what would be the use of that? (Except when building a super intelligent AI, but that did not happen much in our ancestral environment.)
I would worry of conflict of labeling the car choice as incoherent vs the result indicating that the model assumtions were insufficient.
Mathwise the analog seems to pose interesting attack angles. For example as a math question asking whether a gradient accepting or curlless vector field could when projected to lower dimensions aquire curl is probably well posed. The filosophy analog would be that can there be rational behaviour that would appear as irrational to a coarser evaluation threshold.
The curl companion concept divergence might have similar level analogs. Positive divergence would not voluntarily be entered into and negative divergence would not voluntarily be left. Thus given power and time one would expect the system to be found in a negative divergence spot. And a system found in a positive divergence spot was probably forced there.
I’d expect the preference at each point to mostly go in the direction of either axis.
However, this analysis should be interesting in non-cooperative games where the vector might represent a mixed strategy, with amplitude the expected payoff perhaps.
And kudos for the neat explanation and an interesting theoretical framework :)
Thanks!
Do you mean that you expect that at each point, the preference vector will be almost entirely pointed in the x direction, or almost entirely pointed in the y direction, rather than being pointed in a “mixed direction”? If so, why would that be your expectation? To me, it seems very intuitive that people often care a lot about both more wealth and more security, or often care a lot about both the size and the appearance of their car. And in a great deal of other examples, people care about many dimensions of a particular thing/situation at the same time.
Here’s two things you might mean that I might agree with:
“If we consider literally any possible point in the vector field, and not just those that the agent is relatively likely to find itself in, then at most such points the vector will be almost entirely towards one of the axes. This is because there are diminishing returns to most things, and they come relatively early. So if we’re considering, for example, not just $0 to $100 million, but $0 to infinite $s, at most such points the agent will probably care more about whatever the other thing is, because there’s almost no value in additional money.”
“If we consider literally any possible dimensions over which an agent could theoretically have preferences, and not just those we’d usually bother to think about, then most such dimensions won’t matter to an agent. For example, this would include as many dimensions for the number of specks of dust there are on X planet as there are planets. So the agent’s preferences will largely ignore most possible dimensions, and therefore if we choose a random pair of dimensions, if one of them happens to be meaningful the preference will almost entirely point towards that one.” (It seems less likely that that’s what you meant, though it does seem a somewhat interesting separate point.)
No, I was simply mistaken. Thanks for correcting my intuitions on the topic!