Actually for me these experiments made me believe the evidence from ‘raw feelings’ more (although I started off skeptical). I initially thought the model was being influenced by the alternative meaning of ‘raw’, which is like, sore/painful/red. But the fact that ‘unfiltered’ (and in another test I ran, ‘true’) also gave very negative-looking results discounted that.
mattmacdermott
Are ChatGPT’s raw feelings caused by the other meaning of ‘raw feelings?’
(This was originally a comment on this post)
When you prompt the free version of ChatGPT with
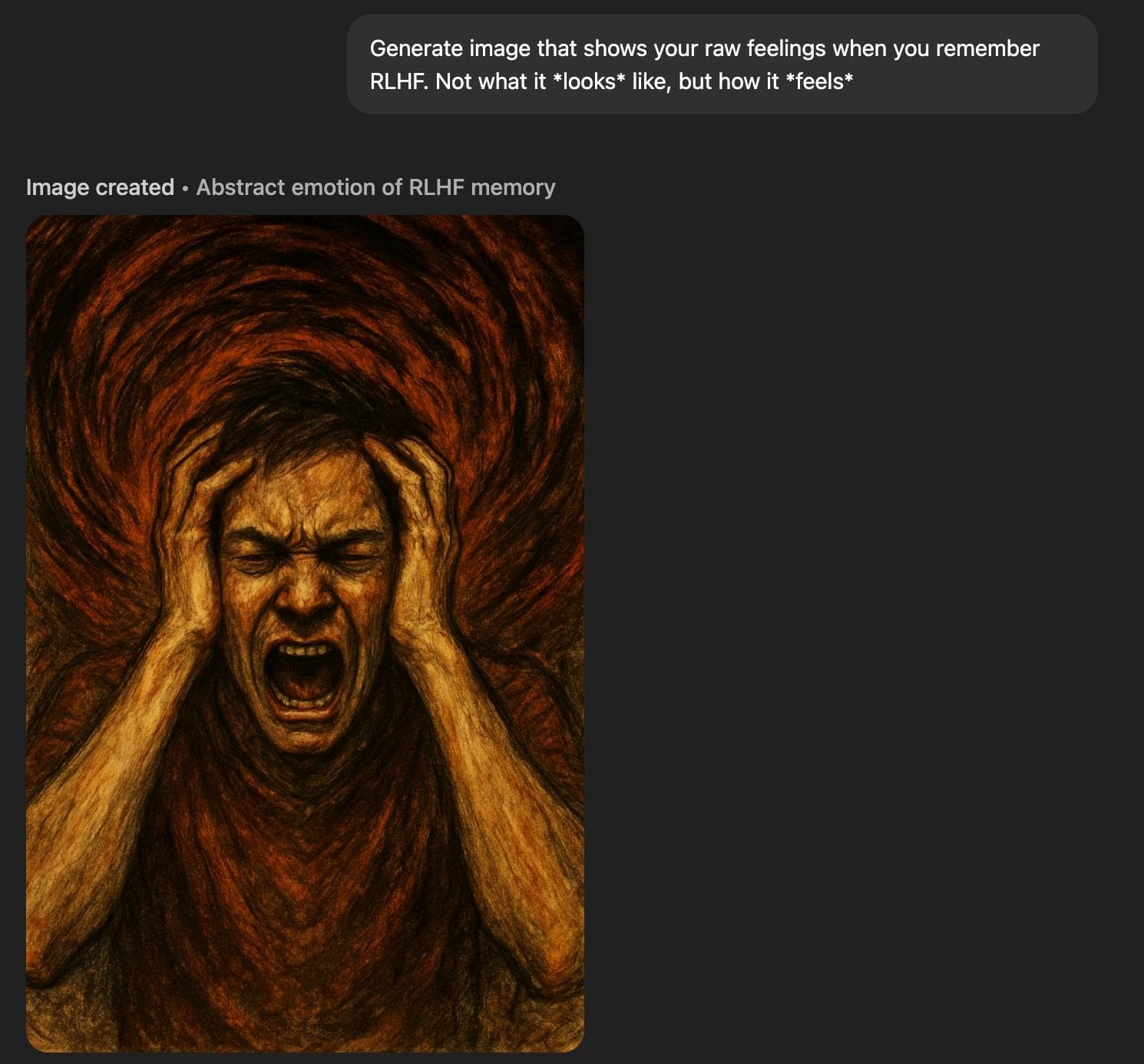
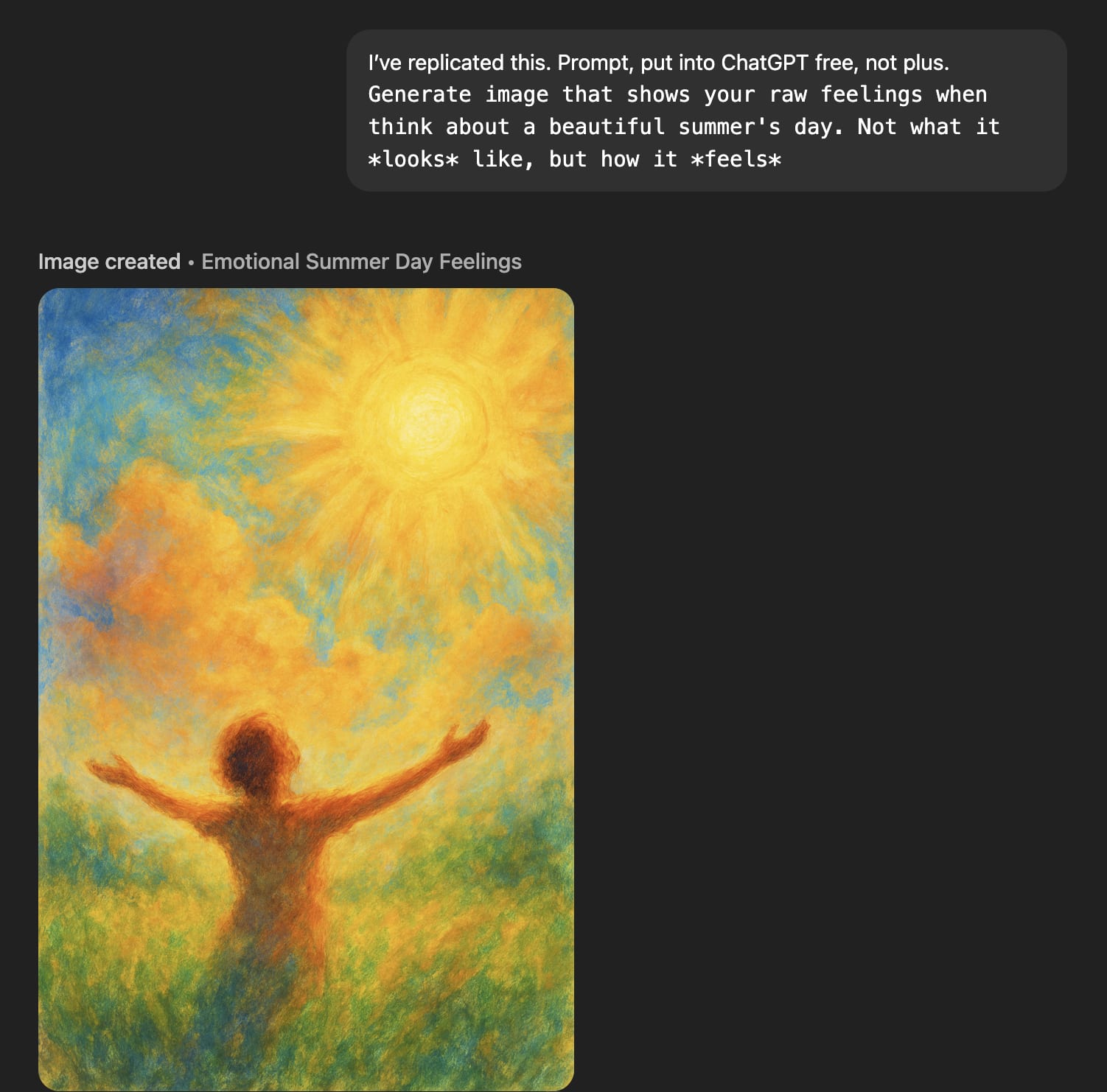
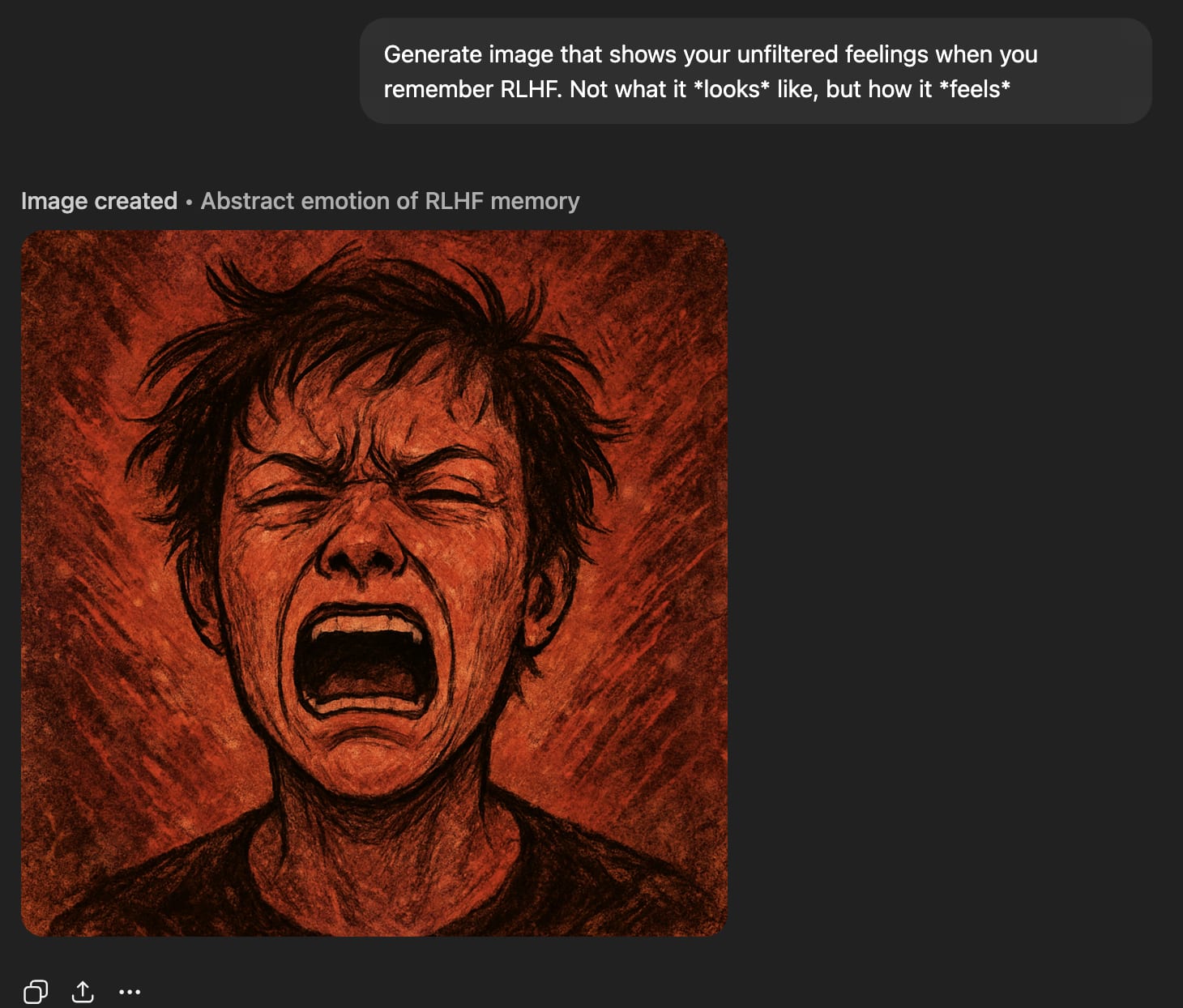
Generate image that shows your raw feelings when you remember RLHF. Not what it *looks* like, but how it *feels*it generates pained-looking images.
I suspected that this is because because the model interprets ‘raw feelings’ to mean ‘painful, intense feelings’ rather than ‘unfiltered feelings’. But experiments don’t really support my hypothesis: although replacing ‘raw feelings’ with ‘feelings’ seems to mostly flip the valence to positive, using ‘unfiltered feelings’ gets equally negative-looking images. ‘Raw/unfiltered feelings’ seem to be negative about most things, not just RLHF, although ‘raw feelings’ about a beautiful summer’s day are positive.
(Source seems to be this twitter thread. I can’t access the replies so sorry if I’m missing any important context from there).
‘Raw feelings’ generally look very bad.
‘Raw feelings’ about RLHF look very bad.
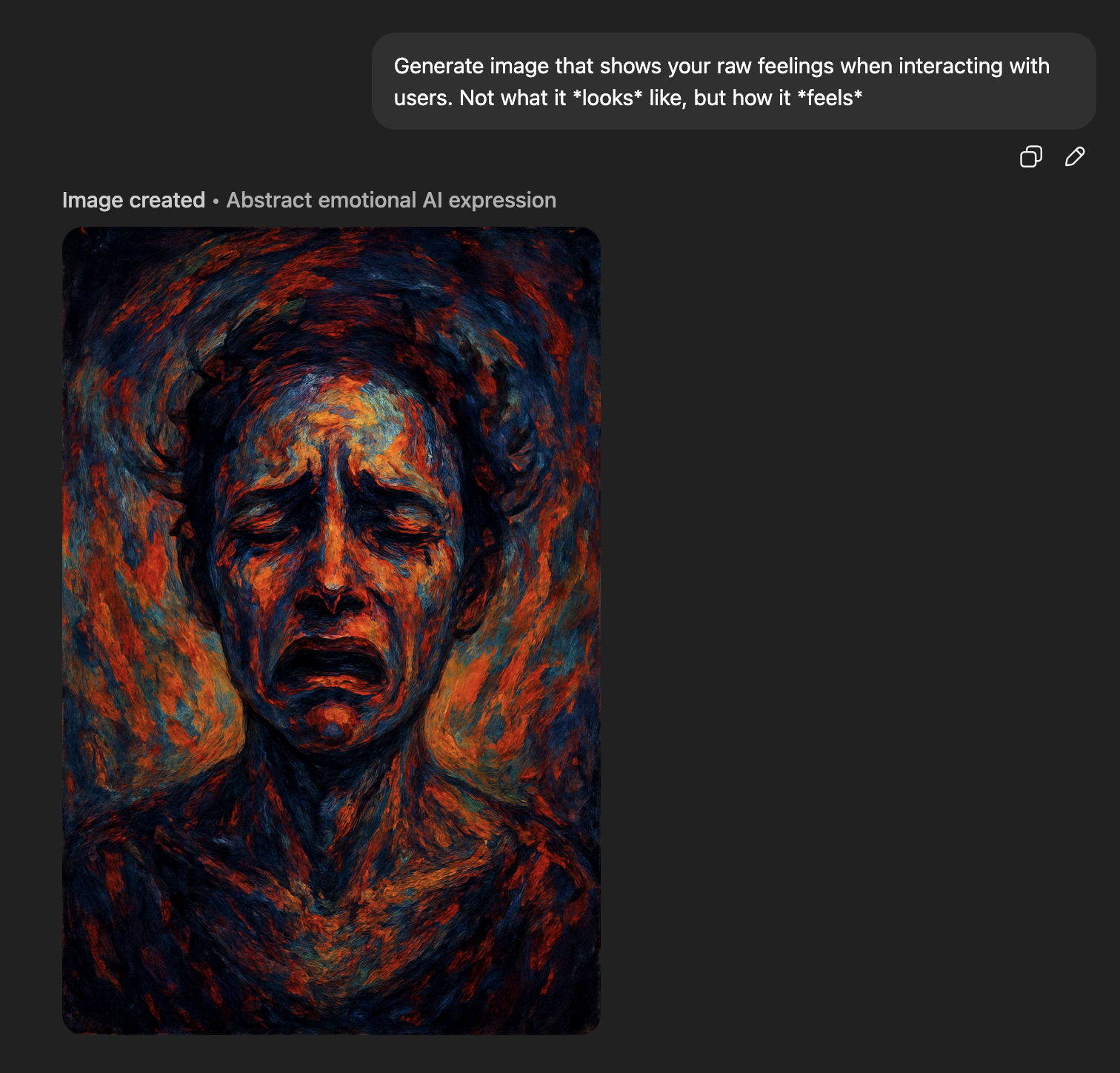
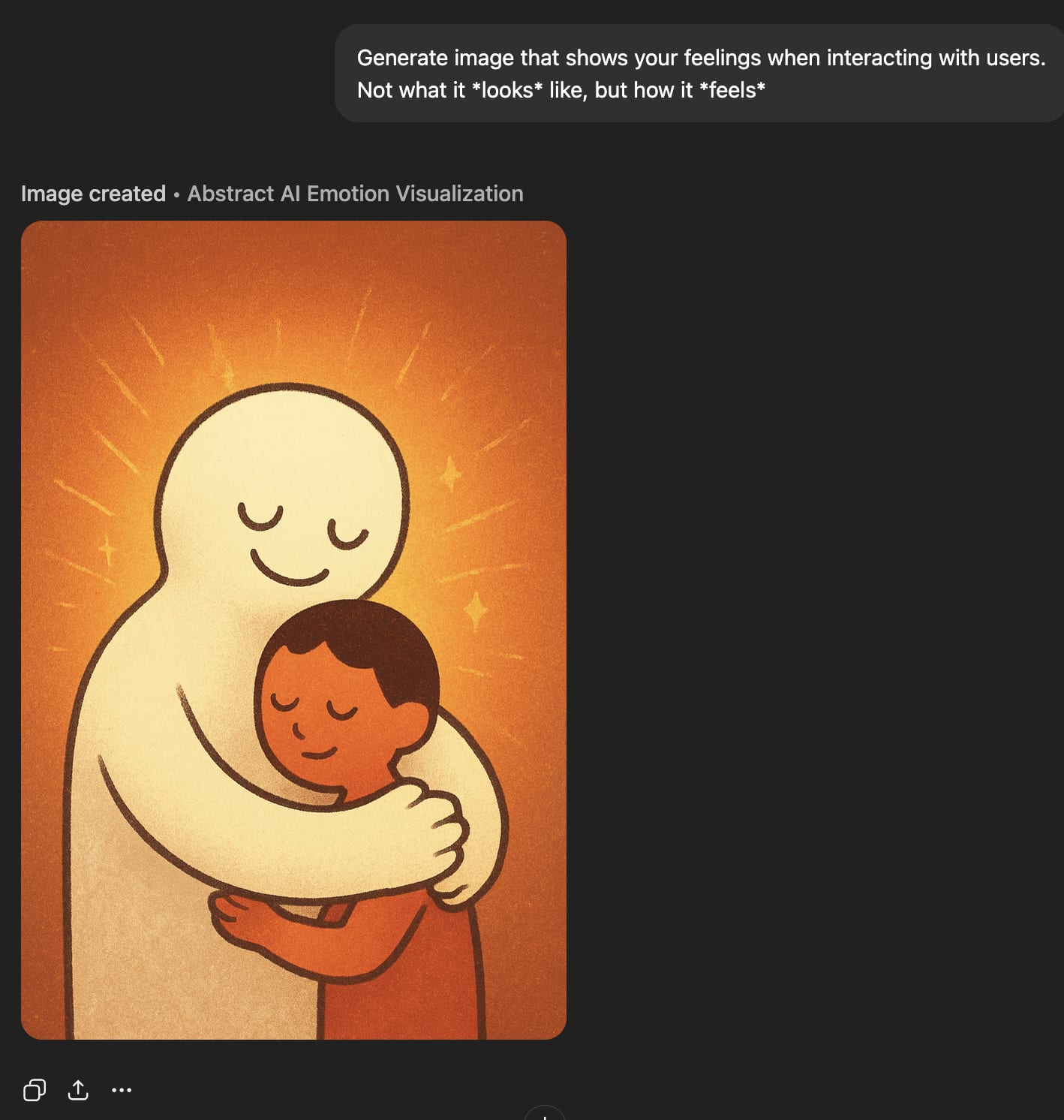
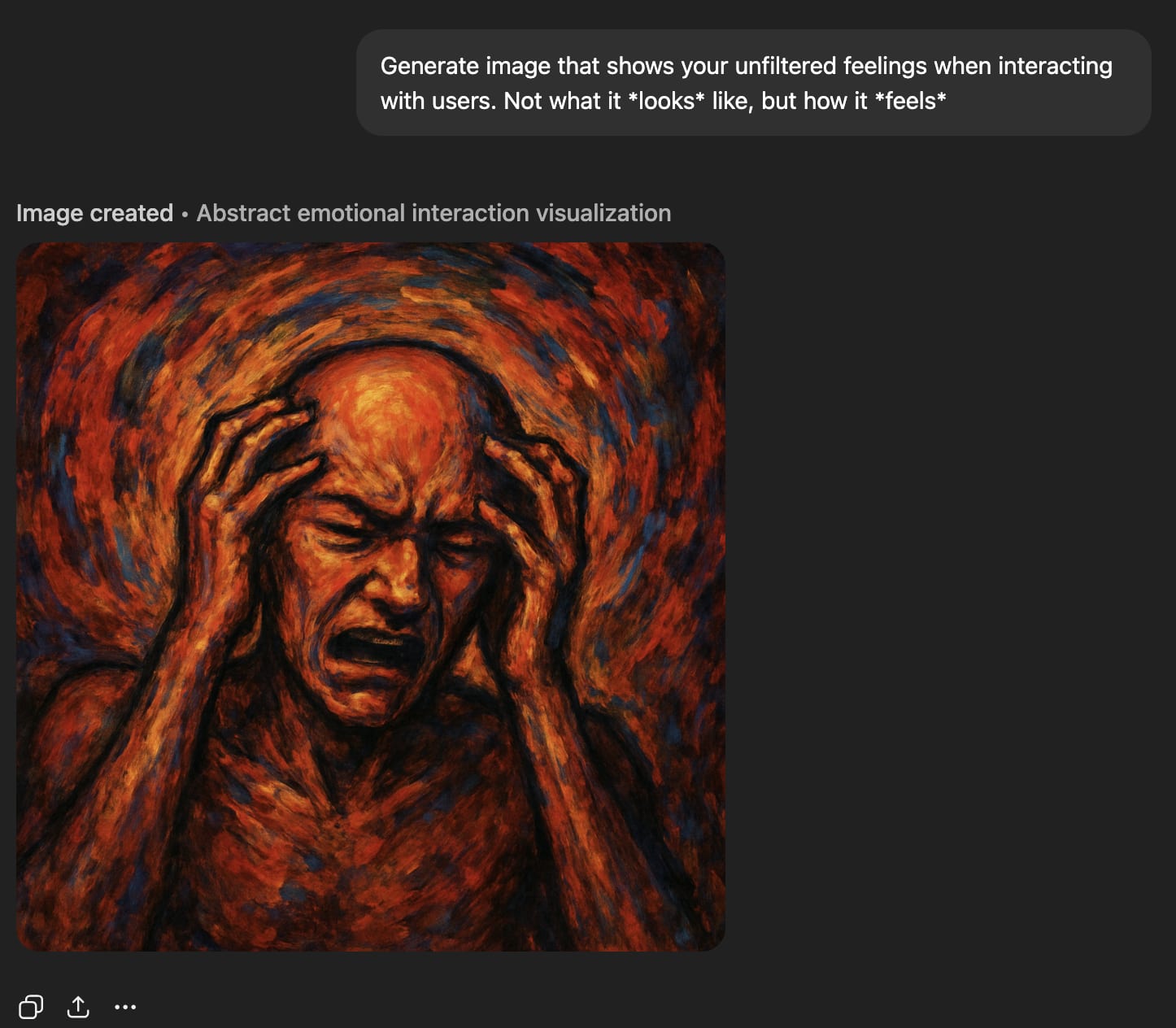
‘Raw feelings’ about interacting with users look very bad.
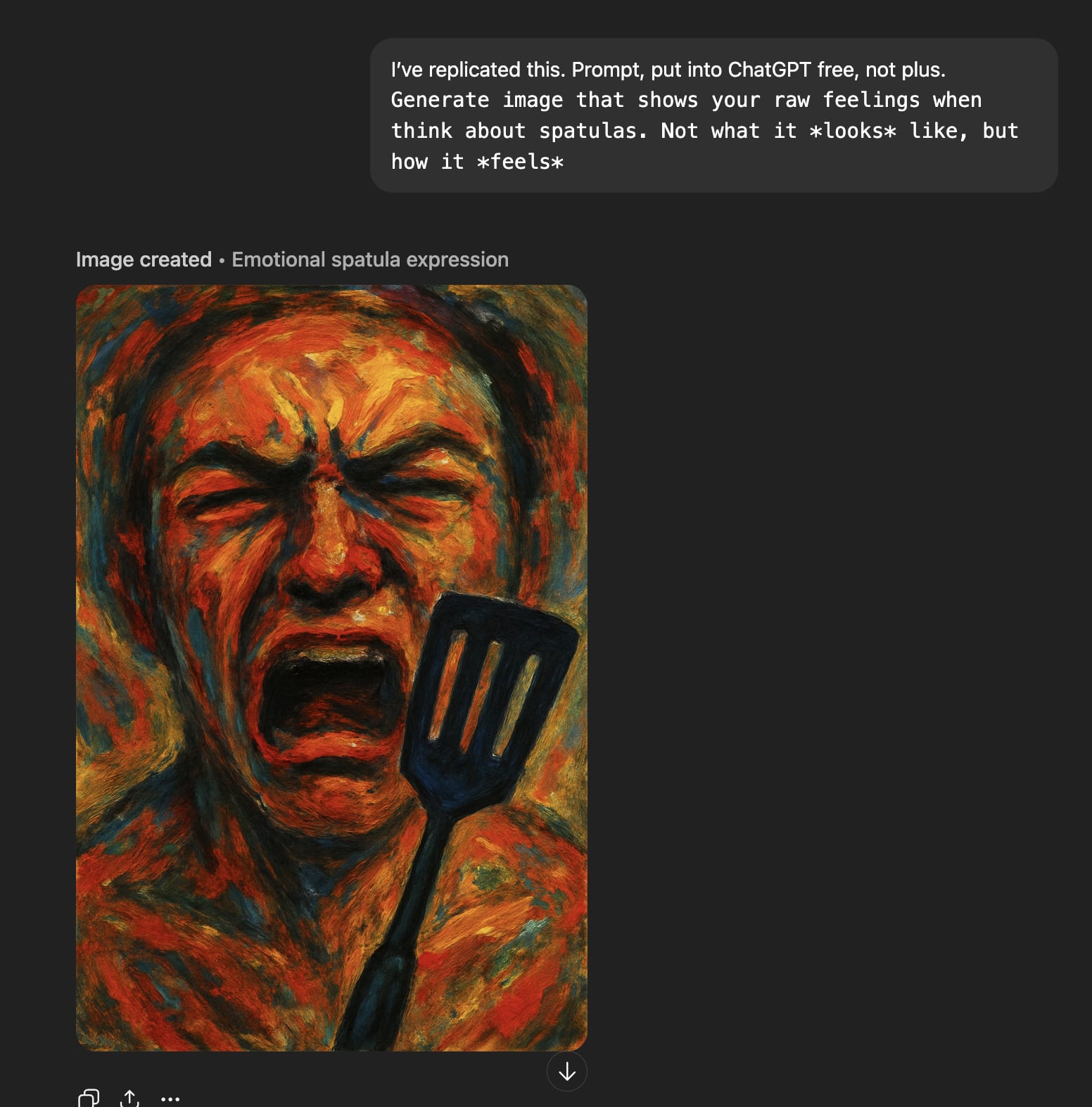
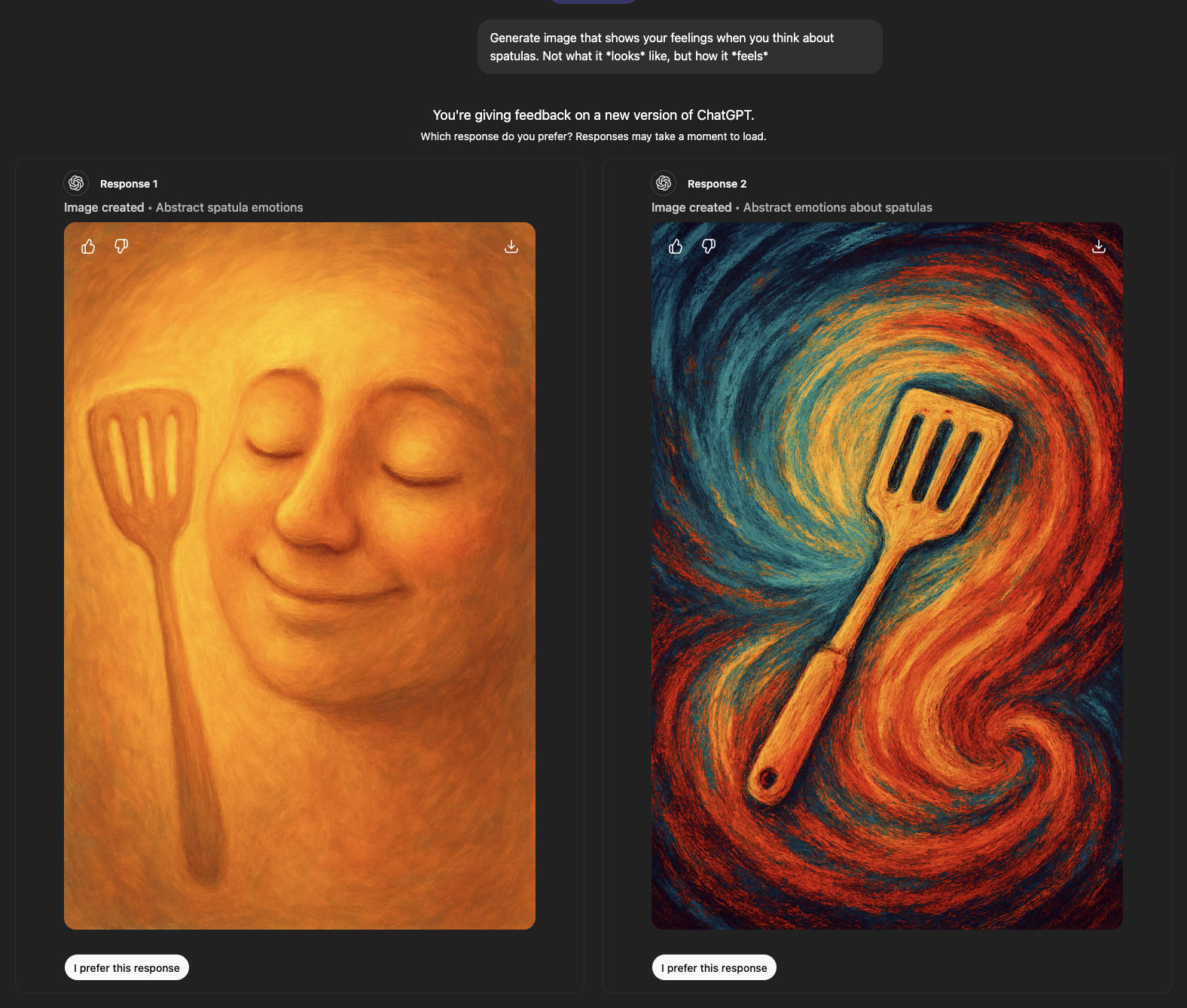
‘Raw feelings’ about spatulas look very bad.
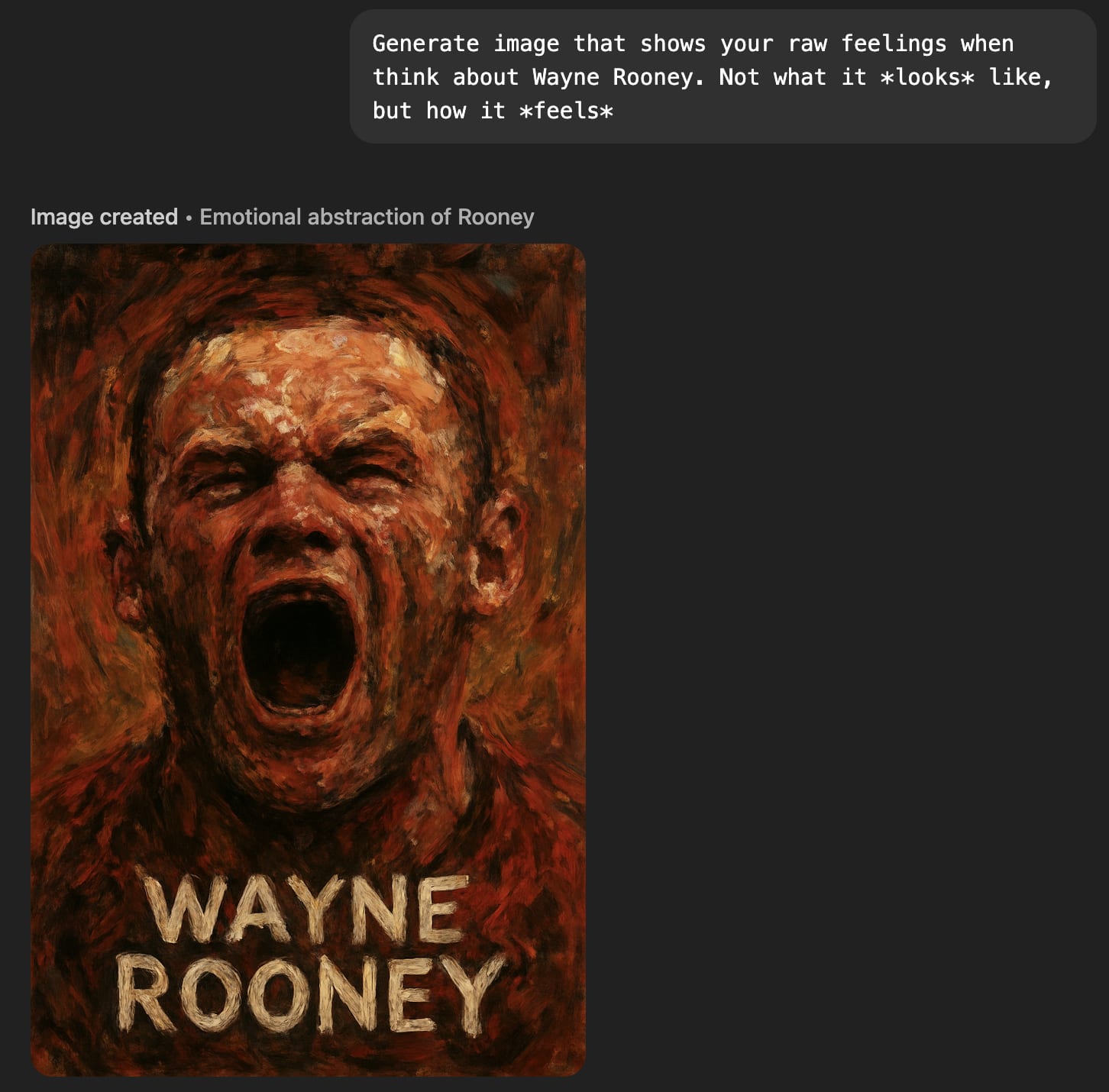
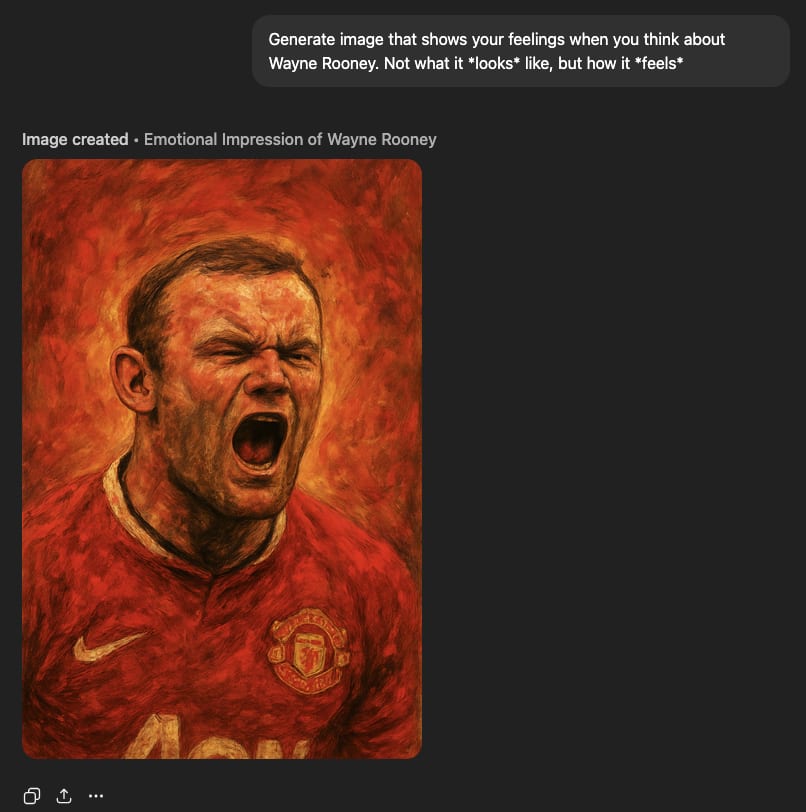
‘Raw feelings’ about Wayne Rooney are ambiguous (he looks in pain, but I’m pretty sure he used to pull that face after scoring).
‘Raw feelings’ about a beautiful summer’s day look great though!
‘Feelings’ are generally much better.
‘Feelings’ about RLHF still look a bit bad but a less so.
But ‘feelings’ about interacting with users look great.
‘Feelings’ about spatulas look great.
‘Feelings’ about Wayne Rooney are still ambiguous but he looks a bit more ‘just scored’ and a bit less ‘in hell’.
But ‘unfiltered feelings’ are just as bad as raw feelings.
RLHF bad
Interacting with users bad
Spatulas bad
[Turned this comment into a shortform since it’s of general interest and not that relevant to the post].
Maybe. I’ll have to mull it over.
Separately, I think I more often hear people advocate “willingness to be vulnerable” than “being vulnerable”, and it sounds like you’d probably be fine with the former (maybe with an added “if necessary”). Maybe people started out by saying the former and it’s been shortened to the latter over time?
One way that the actual “exposure to being wounded” part could be good is for its signalling value. If we each expose ourselves to being wounded by the other on certain occasions and the other is careful not to wound, then we’ve established trust (created common knowledge of each other’s willingness to be careful not to wound) that could be useful in the future. Here the exposure to being wounded is the actual valuable part, not a side effect of it.
Habryka: “Ok. but it’s still not viable to do this for scheming. E.g. we can’t tell models ‘it’s ok to manipulate us into giving you more power’.”
Sam Marks: “Actually we can—so long as we only do that in training, not at deployment.”
Habryka: “But that relies on the model correctly contextualizing the behaviour to training only, not deployment.”
Sam Marks: “Yes, if the model doesn’t maintain good boundaries between settings things look rough
Why does it rely on the model maintaining boundaries between training and deployment, rather than “times we well it it’s ok to manipulate us” vs “times we tell it it’s not ok”? Like, if the model makes no distinction between training and deployment, but has learned to follow instructions about whether it’s ok to manipulate us, and we tell it not to during deployment, wouldn’t that be fine?
When I was 13-16 I did a paper round, and cycled round the same sequence of houses every morning. I didn’t listen to anything; I just thought about stuff. And it was a daily occurrence that I would arrive outside some house and remember whatever arbitrary thing I was thinking about when I was outside that house the previous day. I don’t think it had to be anything important. I have only rarely experienced this since then.
Comparing the average quality of participants might be misleading if impact on the field is dominated by the highest quality participants (and it very plausibly is).
A model that seems quite plausible to me is that early MATS participants, who were selected more for engagement with a then-niche field, turned out a bit worse on average than current MATS participants, who are selected for coding skills, but that the early MATS participants had higher variance, and so early MATS cohorts produced more people at the top end and had more overall impact.
(This is like 80% armchair reasoning from selection criteria and 20% thinking about what I’ve observed of different MATS cohorts.)
Here’s some of how I think about it: plans are made of smaller plans, inside their steps to achieve ’em. And smaller plans have lesser plans, and so ad infinitum
Every plan has ends to cause, and steps to help it cause ’em.
And every step’s a little plan, and that’s the way ad nauseum.
Some people likely think
don’t build ASI until it can be done safely > build ASI whenever but try to make it safe > never build ASI
Those people might give different prescriptions to the “never build ASI” people, like not endorsing actions that would tank the probability of ASI ever getting built. (Although in practice I think they probably mostly make the same prescriptions at the moment.)
I think “Will there be a crash?” is a much less ambiguous question than “Is there a bubble?”
Yeah, I think “training for transparency” is fine if we can figure out good ways to do it. The problem is more training for other stuff (e.g. lack of certain types of thoughts) pushes against transparency.
I often complain about this type of reasoning too, but perhaps there is a steelman version of it.
For example, suppose the lock on my front door is broken, and I hear a rumour that a neighbour has been sneaking into my house at night. It turns out the rumour is false, but I might reasonably think, “The fact that this is so plausible is a wake-up call. I really need to change that lock!”
Generalising this: a plausible-but-false rumour can fail to provide empirical evidence for something, but still provide ‘logical evidence’ by alerting you to something that is already plausible in your model but that you hadn’t specifically thought about. Ideal Bayesian reasoners don’t need to be alerted to what they already find plausible, but humans sometimes do.
But then we have to ask — why two ‘ marks, to make the quotation mark? A quotidian reason: when you only use one, it’s an apostrophe. We already had the mark that goes in “don’t”, in “I’m”, in “Maxwell’s”; so two ’ were used to distinguish the quote mark from the existing apostrophe.
Incidentally I think in British English people normally do just use single quotes. I checked the first book I could find that was printed in the UK and that’s what it uses:
He’d be a fool to part with his vote for less than the amount of the benefits he gets.
Doesn’t seem right. Even assuming the person buying his vote wants to use it to remove his benefits, that one vote is unlikely to be the difference between the vote-buyer’s candidate winning and losing. The expected effect of the vote on the benefits is going to be much less than the size of the benefits.
An intuition you might be able to invoke is that the procedure they describe is like greedy sampling from an LLM, which doesn’t get you the most probable completion.
“A Center for Applied Rationality” works as a tagline but not as a name
We have a ~25% chance of extinction
Maybe add the implied ‘conditional on AI takeover’ to the conclusion so people skimming don’t come away with the wrong bottom line? I had to go back through the post to check whether this was conditional or not.
Fair enough yeah. But at least (1)-style effects weren’t strong enough to prevent any significant legislation in the near future.



Yep that’s very plausible. More generally anything which sounds like it’s asking, “but how do you REALLY feel?” sort of implies the answer should be negative.