Dark Matters
This post will be about the main points of evidence for the existence of dark matter. To evaluate whether a competing theory to dark matter is plausible, it’s important to know what the actual arguments in favor of dark matter are in more detail than just “dark matter is the stuff you have to add to get galactic rotation curves to work out”. A competitor has to address the strongest arguments in favor of the existence of dark matter, not just the weaker fare like galactic rotation curves.
So, when reading some hot new arxiv paper about dark matter or the lack thereof, it is fairly useful to know the top five lines of evidential support for dark matter (in my own personal estimation, others may differ). This lets you at least check whether the result is directly addressing the major cruxes that the case for dark matter rests upon, or just picking off one particular piece of evidence and sweeping the rest under the rug, even if you lack the full technical ability to evaluate the claimed result.
This post will be saving the best for last, so if you’re not going to read the whole thing, skip down to sections 4 and 5.
Also, what exactly is meant when the term “dark matter” is used in this post? Anything with mass (so it’s affected by gravity and gravitationally influences other things) which does not interact via the electromagnetic force. Electrons, protons, nuclei, and atoms emphatically do not count. Black holes, neutrinos, WIMPS (weakly interacting massive particles), and axions would count under this definition. The last two are theoretical, the first two are very much established. Of course, it would be a massive cop-out to go “neutrinos exist, therefore dark matter does”, so “dark matter” will be used with a followup connotation of “and whatever the heck is (we don’t know yet), there must be 5x more of it in the universe than matter made of atoms or atom parts, no way around that whatsoever”
Point 1: Galactic Rotation Curves
The story begins with galaxy rotation curves, which were the original motivation for postulating dark matter in the first place. Given a point gravitational mass, it’s pretty simple to calculate the velocity of something orbiting around it, depending only on how far away the object is orbiting and how much mass is in the central point. Stuff orbiting further out from a point mass will be orbiting at a lower velocity.
With a bit more work, given a disc of mass, you can calculate the velocity of something orbiting around or within it. For this, the graph of orbital velocity vs distance from the center of the disc first rises, then falls. Orbital velocities are low in the center because stuff orbiting near the center of the disc isn’t orbiting around very much mass, and orbital velocities are low at the outside of the disc, because you get closer to being able to approximate things by the situation “your distant object is orbiting around a central point mass”, which, as previously discussed, already exhibits the “stars on further-out orbits move more slowly” behavior.
Computing this in practice requires knowledge of two things, however. First, you need to know how fast the stars in the galaxy are orbiting around the center. Second, you need to know the radial distribution of mass in the disc or ellipse.
It’s pretty easy to tell how fast stars in a galaxy are orbiting around the center, for suitably chosen galaxies. Stars have emission and absorption lines at very specific frequencies measured to very high accuracy, which only depend on details of atomic physics that don’t change in different galaxies. So, as an example, you could pick an edge-on spiral galaxy, and look at the position of the absorption lines in the center of the galaxy. Then, you can look at the two edges of the galaxy, and in one edge, the emission/absorption line will be shifted to higher frequencies (the side of the galaxy that is rotating towards you), and in the other edge which is rotating away from you, the line will be shifted to lower frequencies, and with this you can accurately measure the rotational velocity of stars around the center of the galaxy.
But what about figuring out the radial distribution of mass? Well, for stars, by looking at a bunch of binary stars in the Milky Way, and stellar evolution models, we have an accurate idea how the color of a star corresponds to its mass and luminosity, so if you know how far away a galaxy is, and it has a spectrum corresponding to a bunch of orange K-type stars, you can use how bright the galaxy is, how far away it is, and the luminosity-to-mass relationship for K-type stars to figure out about how much stellar mass is there. It’s more complicated than that because there’s many different types of stars, but it can be done.
Of course, stars aren’t all the mass we know of. In fact, they often make up a rather small portion of the visible mass in a galaxy. There are also clouds of hot ionized hydrogen, which emit high-frequency light, UV and up. And clouds of monoatomic hydrogen can be picked out in the radio spectrum from their characteristic 21-cm radio waves. Similarly, clouds of diatomic hydrogen, , have their own characteristic spectral lines. Just check the luminosity of those vs the distance of the galaxy, and you can figure out about how much gas of the various types there is.
Of course, this might not account for all the mass in a galaxy, there might be some stuff that was missed. But we can try adding up all the mass that we see and where we see it, and check that against the orbital velocity of the stars to see if we found everything or missed some stuff.
And, lo and behold, if you check the speed at which stars orbit in galaxies, it does not exhibit the expected behavior. Yes, orbital velocities are low in the center, but towards the outskirts, where you’d expect most of the mass to be more towards the middle of the galaxy so the stars should be slowing down in their orbits, they’re either orbiting just as fast or even speeding up slightly. We can check even further out by looking at the 21 cm line of cold monoatomic hydrogen, and it’s still rotating fast. Which would all be accounted for by the galaxy being embedded in a big cloud of mass.
On its own, this isn’t terribly convincing. The estimates of the rotation curves rely on us managing to account for all the matter we saw. So maybe there are just big clouds of hydrogen that we haven’t managed to find yet. Yes, there’s a bunch of missing mass, but jumping from that to concluding that it isn’t made of atoms is quite a stretch. Or maybe a full GR (General Relativity) treatment of the galaxy would account for things? Or maybe this is pointing towards a change in the laws of gravity itself on large scales? More on these options later.
For now, I’ll observe something quite interesting. While most galaxies have rotation curves like this which indicate that there’s about 6x more mass there than can be seen (on average), this number certainly isn’t uniform across the universe. It’s a good average for galaxy clusters, but the ratio experiences a lot more variation as the galaxy gets smaller, with the most extreme cases being found in dwarf galaxies. There are some dwarf galaxies where the visible matter pretty much accounts for the galactic rotation curve, and some dwarf galaxies where the rotation curves seem to indicate that there’s >100x more matter there than was observed. So, whatever explanation you invoke to account for galactic rotation curves, it should hopefully account for the existence of the occasional dwarf galaxy where what you see is what you get.
I count this as one of the weaker pieces of evidence in favor of dark matter, partially because it was the piece of evidence that lead to dark matter being postulated in the first place. It does no good to go “look at how dark matter perfectly accounts for galactic rotation curves” when this evidence was what lead to dark matter being promoted to a live hypothesis in the first place.
The other reason why it’s one of the weaker pieces of evidence is that dark matter isn’t a perfect fit, just a pretty good one. Pretty much every competitor theory to dark matter starts out with trying to replicate the galactic rotation curves, and so they also do a fairly good job at it.
Simulations of galactic evolution are quite hard, and the existence of an extended dark matter halo does account for the rotation curves quite well (as it was supposed to do), but there’s two predictions from these simulations which reality doesn’t quite seem to bear out.
The first is the cuspy halo problem. The simulations seem to indicate that there should be a considerable overabundance of dark matter in the core of a galaxy, where empirically it looks more like a uniform distribution given how the stars are moving in there. The best explanation I’ve seen is this paper which indicates it’s a computational artifact of the algorithms used in the simulations to get a massive N-body physics problem down from interactions per timestep to computations per timestep, though I lack the technical expertise necessary to fully evaluate said paper.
The second is the dwarf galaxy problem. The simulations seem to indicate that there should be about 50x more dwarf galaxies around a galaxy than actually seem to exist. From searching harder, we have found more ultra-dim dwarf galaxies around the Milky Way than were thought to exist at the time, and these new ones seem to have very high ratios of dark matter in them by how the stars are moving. So, one of the proposed explanations is that maybe there are in fact a whole bunch of dwarf-galaxy-sized lumps of dark matter around our galaxy that have so little gas and stars associated with them that we don’t know they’re there.
A second possible explanation to the dwarf galaxy problem is warm dark matter. Roughly, if we assume dark matter is made up of a bunch of particles, we’ve got three possibilities. The first is that they’re going near light-speed, as neutrinos do. This is hot dark matter. Or they could be traveling at fairly low velocities, like <10 percent of lightspeed. This is cold dark matter. Or they could be something in the middle, ie, warm dark matter. If all your particles are going super-fast and only interact via gravitation, they would form an enormous spread-out fluffy mass, while if all your particles aren’t going fast at all, gravitation can draw them into much smaller, clumpier, and denser structures.
Hot dark matter is ruled out (well, technically, neutrinos are a form of hot dark matter, but they don’t account for anywhere near the 5x mass excess), as the size of its clumps would be considerably larger than a galaxy, and simulations of galaxy formation with the dark matter being hot don’t produce anything like what we see today. So that rules out neutrinos as a possibility, because if they made up most of the dark matter, you wouldn’t get galaxies looking like they currently do.
Cold dark matter, being much more clumpy, produces that profusion of dwarf galaxies which may or may not exist. So, if the dark matter is warm, it would smooth things out enough to still correctly account for what occurs at the scale of a big galaxy, but not a tiny little dwarf galaxy, as the stuff is moving too fast to form structures of that small size. From talking to someone in the field, apparently cold dark matter is favored, though I’m not entirely sure why. It has a lot more particle candidates from theoretical physics than warm dark matter does, but there’s probably some other reason I missed.
So, for dark matter vs competitors, galactic rotation curves don’t settle it, as all the competitors for dark matter try to explain those rotation curves as well. There’s also some unsolved issues where dark matter accounts for galactic rotation curves, but the simulations don’t quite match up with what we see, what with their cuspy halos and profusion of dwarf galaxies. But then we get into meatier fare.
Point 2: Large-scale Universe Structure
We can run simulations of what the large-scale structure of the universe would look like, starting from the conditions a few thousand years after the Big Bang. Just throw in different amounts of regular matter (hydrogen-helium gas mix), light, dark energy, and matter which doesn’t interact with electromagnetism, introduce some overdensities and underdensities of the magnitude and spacing we see in the Cosmic Microwave Background, and run it with General Relativity (this is more tractable than giving galactic formation the full GR treatment). Then just compare against the observed large-scale structure of the universe, to rule out combinations of these components. We should get a match with the pattern of voids and filaments and their densities and spacing we observe in the universe.
Well, first, how do we know the large-scale structure of the universe? Lots of large-scale automated deep-sky surveys, with redshift as a fairly accurate distance proxy, calibrated against type Ia supernova.
There’s also another neat trick with hydrogen gas. If you have some super-bright source of high-energy radiation, like a quasar (the brightest things in the universe), and the light passes through a cloud of neutral hydrogen gas, the hydrogen gas will absorb a particular frequency of UV light. Also, the expansion of the universe doesn’t just redshift light because the galaxy is traveling away from us, it also redshifts light because the light literally stretches out due to the expansion of space over the course of its journey across the universe.
So, if you’ve got a quasar, and the light passes through a cloud of hydrogen gas, that particular UV frequency of light will get absorbed, making a spectral line. Then, if the light keeps going and redshifting and runs into another cloud of hydrogen gas in its travels, the old UV spectral line will have been redshifted down, and light which used to be above that particular spectral line will get redshifted to line up with that frequency of light. So now, looking at the quasar spectrum, there are two absorption lines, the lower one for when the light first went through a cloud of hydrogen, and the higher one for when the light more recently went through a hydrogen cloud. Although, usually, there’s a lot more than two lines. By looking at how deep the absorption lines are in the spectrum, and where they are, you can build up a picture of how much cold hydrogen gas is at what distances along the line-of-sight between us and the quasar.
So, how do the simulations do at reproducing what we see in the universe around us? Well, first-up, this is an opportunity to falsify the usual picture of dark matter. If a 5-to-1 ratio of dark matter to hydrogen/helium gas doesn’t replicate the large-scale structure of the universe, the theory dies right here.
Since I’m citing this as a piece of evidence, it obviously must have passed. In fact, this was known as a problem early on, that for the standard accounting of known mass in the universe, it wasn’t enough to permit large clusters and walls of galaxies to form. The ordinary matter would be too spread out and you’d just get little clumps of galaxies instead of the larger superclusters and walls. That was another reason dark matter was an attractive hypothesis, because if there’s a lot more mass in the universe, you could get enough mass for large-scale structure formation. The dark matter would gravitate into clumps, which would provide a big gravitational well for the ordinary matter to accrete at the bottom of and form galaxies. At the time, this wasn’t super-detailed, the more detailed computer simulations and large-scale surveys of the cosmos (which, again, could have falsified dark matter being in 5x abundance) came afterwards.
This is not accounted for by just gravitoelectromagnetic effects. Modified gravity theories also have a hard time explaining this one. It still leaves open the possibility that maybe there’s just a whole boatload of extra hydrogen and helium out there that we just haven’t spotted yet for whatever reason.
So that’s the second line of evidence, large-scale simulations of the universe most accurately replicate its structure with about 6x more matter than is currently accounted for.
Point 3: Galactic Cluster Lensing
And now we get into the third thing, to further drive the nail into gravity-based competitors.
One of Einstein’s famous original predictions was of the magnitude of displacement of the image of a star from its usual position during a solar eclipse, due to gravitational lensing from the sun. GR passed with flying colors. So, another concievable test that you can carry out for dark matter (once you gain a Hubble Telescope to play around with) is to find a bunch of galaxy clusters which are big enough to have gravitational lensing effects, and see how much of a dent they make in the images of the background galaxies. If it indicates that there’s 6x more matter than you see, then that’s another test passed.
Much of the visible mass in a galactic cluster is in the form of hot plasma which emits X-rays and UV light, from the galaxies moving around and running into each other at high speed which heats up their surrounding gas. This can be weighed by checking the plasma luminosity, and using the spectra to infer temperature of the gas and how brightly it should be glowing, and then if you know far away the galactic cluster is, you can solve for the amount of plasma present.
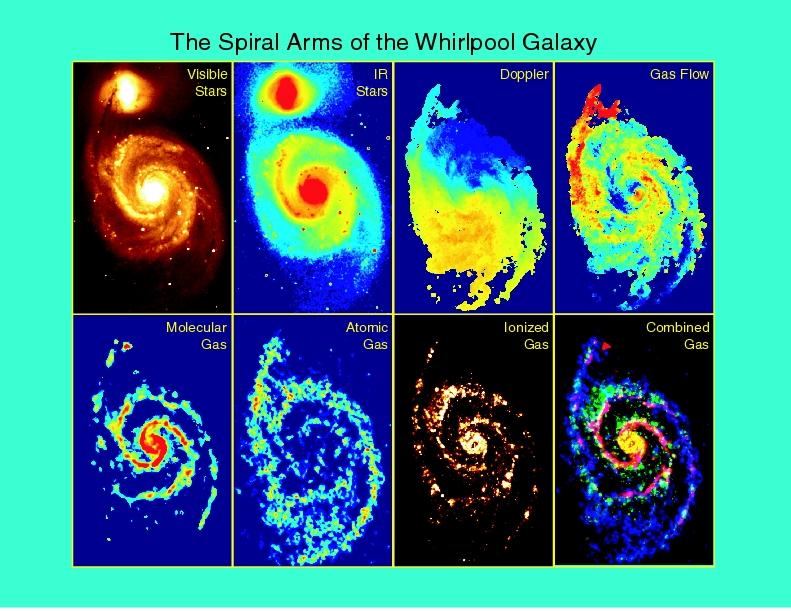
A bunch of studies on this are carried out using weak lensing, which looks at subtle distortions of the background galaxies, but there are galactic clusters with far more spectacular instances of gravitational lensing, as pictured below.

And, what do you know, the gravitational lensing of galaxy clusters all indicate a mass about 6x more than the hot gas and stars and every other detectable source of mass would indicate. Again, this is another thing that modified gravity theories really struggle to deal with. They ace the galactic rotation curves, but don’t do so well with galaxy cluster dynamics.
Point 4: The Bullet Cluster
And while we’re on the topic of galaxy clusters, there’s also the Bullet Cluster. Which wasn’t exactly an advance prediction, but it’s another thing that’s really hard for competitors to explain, while the standard picture of dark matter makes perfect sense of it.
Pretty much, the Bullet cluster is a pair of galaxy clusters that rammed into each other. Stars are very widely spaced. If the Milky Way and Andromeda collided, there would only be about one stellar collision in the whole interaction, IIRC. So the stars should mostly just go through each other. If dark matter mostly doesn’t interact with itself, the dark matter blobs should just go through each other. The same cannot be said for the hot ionized plasma which makes up much of the mass in a galactic cluster, however. The particles in it are charged, and would, with high probability, get slowed down and heated up from ramming into a galactic-cluster-sized blob of hot plasma heading the other way.
And so, we can view the cluster in X-rays to see where most of the visible mass, including stars, is. And we can check the subtle gravitational lensing of background galaxies to see where the actual mass is. And now… check out the following image. Pink is the X-ray emitting gas, purple is where the mass is according to background gravitational lensing.

Explain this with modified gravity.
This also weighs against the “maybe it’s just a bunch of ordinary hydrogen and helium in some gas form we can’t see” hypothesis, because it’s rather hard to shoot two galaxy-cluster-sized blobs of gas of each other and have them pass straight through each other.
Point 5: The CMB Power Spectrum
And now we come to my personal favorite piece of evidence. The Bullet cluster is usually taken as the most spectacular line of evidence for dark matter, but the CMB power spectrum is what lets us conclusively rule out that dark matter is anything born of atoms.
This was very much an advance prediction. The detailed measurements of the pattern of ripples in the cosmic microwave background (CMB) radiation, in enough detail to get the following graph, were not around at the time dark matter was postulated. It came in around 2000 and later, mostly from the WMAP probe, and was then refined by the Planck probe.
Roughly, this graph is telling you the magnitude of the fluctuations on different scales of the cosmic microwave background. On the far left of this graph, it’s plotting the amplitude of CMB variations over larger regions of space, where the cosmic microwave background looks pretty uniform. On the far right of this graph, it’s plotting the amplitude of CMB variations on the smallest scales. It says that most of the fluctuations in the CMB are accounted for on the scale of about 1 degree. This spectrum encodes information about what was going in the early universe, the characteristic length scale on which the universe had ripples during its formation.

The positioning of the first peak tells you about the curvature of the universe. It’s the dominant length scale on which the universe has clumps or voids. This can be measured now, from large-scale universe structure. If the first peak was shifted to the left or right, it would correspond to the major fluctuation scale of the universe looking bigger/smaller at early times than it does now, which is characteristic of large-scale universe curvature. The universe, as near as we can tell, looks flat (ie, like , euclidean 3-space) on large scales. The curvature of the universe depends on what it has in it. A universe with a whole bunch of matter/energy in it would be positively curved. The energy in empty space which would account for the cosmological constant (whatever the hell it comes from), accounts for 69% (plus or minus 0.6%) of the total mass-energy budget you need for a flat universe. And, you guessed it, for the remaining known mass, you don’t get anywhere near the 31% necessary.
But this isn’t the only way that you can check up on dark matter with the CMB power spectrum! In the early universe, everything was hot and dense and there was a lot of radiation/light around. So, matter which interacts with radiation would heat up and expand back again if it started compressing, while matter which doesn’t interact with light but does interact with gravity wouldn’t have that effect. Having different amounts of ordinary atomic matter vs dark matter early on in the universe produces different characteristic patterns in the spectrum, with ordinary atomic matter tending to enhance the even-numbered peaks, and dark matter tending to enhance the odd-numbered ones.
And, lo and behold, the CMB power spectrum (particularly the second and third peaks) perfectly fits with ~5% of the universe’s mass-energy being accounted for by matter, and ~26% of the universe’s mass-energy being accounted for by dark matter, summing up to 31%.
This is how we know dark matter can’t be anything made of atoms. Early on in the universe, it was more of a very hot homogenous soup, so everything made of atoms in the current day was in the form of a hot dense soup of gas way back when. So this is directly measuring the proportion of “matter made of atoms” to ”??? stuff that has gravity but doesn’t interact with light”. And it fits!
From an advance-prediction standpoint, we get something else interesting. The CMB ripples seemed to indicate that there was more baryonic (hydrogen and helium) matter in the universe that had previously been accounted for around galaxies, which was promptly dubbed the “Missing Baryon problem”. It was a bit tricky to account for, because much of it was in the form of incredibly wispy warm hydrogen in great streamers between the galactic clusters and in the voids, but by 2020, the last missing 30% of the CMB-indicated hydrogen and helium was accounted for and the missing baryon problem was solved.
Conclusion:
So, the five main lines of support for dark matter are: galactic rotation curves, accurately replicating the large-scale structure of the universe in simulations, the extra mass still being present when you look at galaxy cluster lensing, the bullet cluster having the mass and the visible gas in different locations, and finally, perfectly accounting for the pattern of ripples in the cosmic microwave background in two different ways.
So, this should hopefully provide some background on why dark matter is widely accepted to be a Thing, and furnish some useful heuristics on reading a paper on competitors to dark matter for explaining things. If they only talk about galactic rotation curves and don’t try to explain the CMB spectrum and Bullet Cluster, you can safely throw the paper in the trash, as these are the two major hurdles that the dark matter competitors fail to clear. Conversely, if there’s a paper proposing an alternative to dark matter that manages to explain the CMB power spectrum and the Bullet Cluster, it’s now safe to take it more seriously. It’s the astrophysics equivalent of Scott Aaronson’s heuristics on whether a P vs NP proof is worth taking seriously.
But what even is dark matter, anyways? Well… there are a lot of possibilities, and it would be premature to conclude that it’s any particular one of them, or even that we won’t get hit with something out of left field. The basic constraints we know are: It’s affected by gravity and has gravity. It doesn’t interact through electromagnetism, otherwise it wouldn’t be consistent with the CMB spectra. If it does interact through the weak or strong force, the interaction will be really weak, because we’ve built a bunch of big particle detectors to check for dark matter with appreciable weak or strong force interactions and haven’t come up with shit. Dark matter shouldn’t be hot/travel at a sizeable chunk of the speed of light, because otherwise the large-scale structure of the universe would be too uniform and galaxies wouldn’t have the structure they do, which rules out neutrinos. And you should be able to fire two big lumps of it at each other and have them pass straight through each other, because the Bullet Cluster is a thing.
Hopefully this post was informative.
- How do you feel about LessWrong these days? [Open feedback thread] by (5 Dec 2023 20:54 UTC; 108 points)
- [Intuitive self-models] 1. Preliminaries by (19 Sep 2024 13:45 UTC; 99 points)
- 's comment on Limitations on Formal Verification for AI Safety by (21 Aug 2024 2:55 UTC; 15 points)
- What does “the universe is quantum” actually mean? by (22 Jul 2024 11:52 UTC; 2 points)
- 's comment on Ethics in Many Worlds by (28 Apr 2021 9:57 UTC; 2 points)
This is fabulous content; thank you. I knew virtually nothing about the evidence for dark matter and now feel like I know a fair amount.
One hangup: I’m missing one or more inferential steps in interpreting the picture of the Bullet Cluster. I understand that the pink is gas and purple is mass, but I am not getting how that relates to dark matter. Since the rest of the piece is very explicitly “if A then B because x, A is true because y, therefore B” in spelling out the thought-steps, could you really break it down for the poets in the back? Maybe after “Explain this with modified gravity.”
I’d be interested in an explainer about the theories of what dark matter might be, if there are major schools of thought. (If it’s just people’s pet theories, no need to bother.)
Yes, pink is gas and purple is mass, but also the gas there makes up the dominant component of the visible mass in the Bullet Cluster, far outweighing the stars.
Also, physicists have come up with a whole lot of possible candidates for dark matter particles. The supersymmetry-based ones took a decent kicking at the LHC, and I’m unsure of the motivations for some of the other ones, but the two that look most promising (to me, others may differ in opinion) are axions and sterile neutrinos, as those were conjectured to plug holes in the Standard Model, so they’ve got a stronger physics motivation than the rest. But again, it might be something no physicist saw coming.
For axions, there’s something in particle physics called the strong CP problem, where there’s no theoretical reason whatsoever why strong-force interactions shouldn’t break CP symmetry. And yet, as far as we can tell, the CP-symmetry-breakingness of the strong-force interaction is precisely zero. Axions were postulated as a way to deal with this, and for certain mass ranges, they would work. They’d be extremely light particles.
And for sterile neutrinos, there’s a weird thing we’ve noticed where all the other quarks and leptons can have left-handed or right-handed chirality, but neutrinos only come in the left-handed form, nobody’s ever found a right-handed neutrino. Also, in the vanilla Standard Model, neutrinos are supposed to be massless. And as it turns out, if you introduce some right-handed neutrinos and do a bit of physics fiddling, something called the seesaw mechanism shows up, which has the two effects of making ordinary neutrinos very light (and they are indeed thousands of times lighter than any other elementary particle with mass), and the right-handed neutrinos very heavy (so it’s hard to make them at a particle accelerator). Also, since the weak interaction (the major way we know neutrinos are a thing) is sensitive to chirality, the right-handed neutrinos don’t really do much of anything besides have gravity and have slight interactions with neutrinos, with are already hard to detect. So that’s another possibility.
Additionally, there’s no reason to assume that all dark matter is just one thing. There could be multiple things going on, as long as most of the things going on don’t self-interact.
Heck, for that matter there could be a small (!) dark sector that DOES self-interact as long as its total mass was within the error bars for baryonic mass inferred from primordial nucleosynthesis.
I think what’s happening is basically that the pink shows where the visible mass is, but the purple shows where the mass should be according to gravitational lensing. Dark matter should pass straight through, and that is what we see according to lensing, even though the pink lags behind because it can collide (since it’s mostly the hot plasma).
At least, I think that’s what’s happening… I myself am really confused and am pretty unconfident in that explanation.
I’m also confused as to what modified gravity predicts, and how bullet clusters disprove it. I guess what we’d see is that modified gravity would alter the gravity around the visible mass, not just make it magically act like it just passed through. Ie, a lot about gravity would have to change for such a drastic difference between the mass as perceived through x-rays and the mass as perceived through gravitational lensing.
Here’s a link that seems to confirm what I wrote: https://chandra.harvard.edu/graphics/resources/handouts/lithos/bullet_lithos.pdf
Curated. This was an accessible yet technically precise overview of the evidence surrounding an open research area in physics / cosmology, and I’d like to see more of this sort of post on LW. I think had almost anyone tried this they would have made a really long post with lots of hard technical math and it wouldn’t have been understood by many, so thanks.
Some comments informed by Stacy McGaugh’s blog (you may know most of this already):
The rotation curves show a very tight dependence on the amount of baryonic matter alone, something which you might expect from modified gravity sourced by baryonic matter, but not so much, from ordinary gravity sourced by a mixture of baryonic matter and dark matter.
Lensing is a relativistic effect. The leading phenomenological theory of modified gravity here, MOND, is Modified Newtonian Dynamics, i.e. is defined for the nonrelativistic regime (since the rotation curves involve very small accelerations). So lensing predictions will depend on the specific relativistic extension of MOND. Incidentally, a very recent relativistic extension of MOND (“RelMOND”) is supposed to get that third CMB peak right.
McGaugh seems to regard the possibilities of structure formation in MOND as barely studied, at least when compared to Lambda CDM; and points out that the “21 cm anomaly” could be explained by there being no dark matter in the early universe.
In general, McGaugh cautions that the dark matter paradigm contains numerous parameters which keep being adjusted to match the latest data; whereas in the realm of rotation curves, MOND makes successful significant predictions; but people prefer to keep tweaking Lambda CDM, rather than trying to build on MOND’s successes.
Further comments from me:
I am agnostic about which paradigm is right—clearly they both have their merits—and a middle ground of “MOND-like DM” (e.g. Khoury’s superfluid DM, postulated to have an interaction with baryonic matter that reproduces the MOND gravitational profile) or “DM-like MOND” (e.g. Bullet Cluster lensing from flux in extra metric degrees of freedom?) is also intriguing. Either way, at the galactic scale, there seems to be a relationship between amount of baryonic matter, and strength of these dark effects, that is not explained by ordinary theories of dark matter.
I’m quite curious about whether RelMOND matches the CMB spectrum nearly as well as Lambda-CDM (which has what, 3 free parameters for dark matter and dark energy?), and how much work they had to do to get it to agree. Like, if all you care about is galaxy rotation curves, it’s easy to say that dark-matter-theorists keep changing the amount of dark matter they say is in galaxies to match observations (while, symmetrically, baryonic-matter-theorists keep changing the amount of non-visible baryonic matter they say is in galaxies to match observations). But the CMB is significantly more tightly constrained.
I found this Quanta magazine article about it which seems to indicate that it fits the CMB spectrum well but required a fair deal of fiddling with gravity to do so, but I lamentably lack the physics capabilities to evaluate the original paper.
What we all want to know, of course, is whether Ludwig’s recent paper (which treats only the galactic rotation curve) stands up.
Note that he is not proposing a new theory, only applying standard GR, and claiming to do so correctly for the first time.
This was fantastic, and still leaves me with a conclusion that “dark matter” isn’t a specific hypothesis, it’s a set of reasons to think we’re missing something in our theories which isn’t modified gravity.
That is, saying “Given that everything we see is consistent with Gravity being correct, we conclude that there is not enough baryonic matter to account for what we see,” doesn’t prove the existence of large amounts of non-baryonic matter. Instead, the evidence provides strong indication that either A) there is something we can’t see that has some properties of non-baryonic matter, or B) something is wrong with some theory which isn’t what people propose as modified gravity. We knew enough to say that decades ago. We’ve looked for every type of non-baryonic matter we can think of, and have only been able to eliminate possibilities. The evidence is still pointing to “something else,” and we have some actual or claimed physical objects that aren’t actually prohibited as an answer—but nothing pointing to them.
This sounds a lot like what we would have said pre-special relativity about Galileo’s relativity (which Newton hated because it didn’t allow distinguishing between relative and absolute motion,) and electromagnetism, which didn’t seem to follow the rules for indistinguishability of relative and absolute motion, but was much too good of a theory to be wrong.
Pre-Einstein, we had good reasons to think there’s something there that lets relativity and Maxwell be consistent, but don’t know what it is. They DID have reason to think the answer wasn’t “Maxwell was wrong about the absolute speed limit for light,” just like we know the answer isn’t “gravity just works differently,” but actually plugging the hole required a new conceptual model.
In Bayesian terms, we should have some prior on “gravity + visible mass,” some prior on “modified gravity,” some prior on “invisible mass that accounts for observation,” and some prior on “something else will be found for a theory”, and every piece of evidence seems like it’s at least as strong evidence for #4 as it is for #3, and our continued lack of success finding the former best candidates for what the invisible mass is made of is better evidence for #4 than #3.
If there’s something wrong with some theory, isn’t it quite odd that looking around at different parts of the universe seems to produce such a striking level of agreement on how much missing mass there is? If there was some out-of-left-field thing, I’d expect it to have confusing manifestations in many different areas and astronomers angsting about dramatically inconsistent measurements, I would not expect the CMB to end up explained away (and the error bars on those measurements are really really small) by the same 5:1 mix of non-baryonic matter vs baryonic matter the astronomers were postulating for everything else.
In other words, if you were starting out blind, the “something else will be found for a theory” bucket would not start out with most of its probability mass on “and in every respect, including the data that hasn’t come in yet since it’s the 1980′s now, it’s gonna look exactly like the invisible mass scenario”. It’s certainly not ruled out, but it has taken a bit of a beating.
Also, physics is not obligated to make things easy to find. Like how making a particle accelerator capable of reaching the GUT scale to test Grand Unified Theories takes a particle accelerator the size of a solar system.
“isn’t it quite odd that looking around at different parts of the universe seems to produce such a striking level of agreement on how much missing mass there is?”
But they don’t. Dark matter, as a theory, posits that the amount of mass that “must be there somewhere” varies in amount and distribution in an ad-hoc fashion to explain the observations. I think it’s likely that whatever is wrong with the theory, on the other hand, isn’t varying wildly by where in the universe it is. Any such explanation would (need to) be more parsimonious, not less so.
And I agree that physics isn’t obligated to make things easy to find—but when the dark matter theory was postulated, they guessed it was a certain type of WIMP, and then kept not finding it. Postulating that it must be there somewhere, and physics doesn’t need to make it easy, isn’t properly updating against the theory as each successive most likely but still falsifiable guess has been falsified.
Most physicists actually have updated—if you listen to Sean Carroll’s podcast, he just this week talked about how when the LHC started up he thought there was about a 60% chance of finding a dark matter candidate, and that he’s updated his views in light of our failure to find it. But he also explained that he still thinks dark matter is overwhelmingly likely (because of evidence like that explained in the post).
That’s good to hear. But if “he started at 60%,” that seems to mean if he “still thinks dark matter is overwhelmingly likely” he is updating in the wrong direction. (Perhaps he thought it was 60% likely that the LHC found dark matter? In which case I still think that he should update away from “overwhelmingly likely”—it’s weak evidence against the hypothesis, but unless he started out almost certain, “overwhelmingly” seems to go a bit too far.)
Yes, 60% that the LHC would find a dark matter candidate. Anyhow, maybe you should take away that this emphasizes that he does (and cosmologists in general do) have lots of evidence.
Good post. Makes a good case. I wasn’t aware of the evidence from galactic cluster lensing; that’s pretty impressive. (I guess not as much as the CMB power spectrum, but that I’d heard about before. :P )
But, my understanding is that the Bullet Cluster is actually not the strong evidence it’s claimed to be? My understanding of modified gravity theories is that, since they all work by adding extra fields, it’s also possible for those to have gravity separated from visible matter, even if no dark matter is present. (See e.g.. here… of course in this post Hossenfelder claims that the Bullet Cluster in particular is actually evidence against dark matter due to simulation reasons, but I don’t know how much to believe that.)
Of course this means that modified gravity theories also aren’t quite as different from dark matter as they’re commonly said to be—with either dark matter or modified gravity you’re adding an additional field, the difference is just (OK, this is maybe a big just!) the nature of that field. But since this new field would presumably not act like matter in all the other ways you describe, my understanding is that it is still definitely distinct from “dark matter” for the purposes of this post.
Apparently these days even modified gravity proponents admit you still need dark matter to make things work out, which rather kills the whole motivation behind modified gravity, so I’m not sure if that’s really an idea that makes sense anymore! Still, had to point out the thing about the Bullet Cluster, because based on what I know I don’t think that part is actually correct.
And with enough epicycles you can fit the motion of planets with geocentricism. If MOND supporters can dismiss Bullet Cluster they’ll dismiss any future evidence, too.
I just explained why (without more specific theories of in exactly what way the gravity would become delocalized from the visible mass) the bullet cluster is not evidence one way or the other.
Now, you compare the extra fields of modified gravity to epicycles—as in, post-hoc complications grafted on to a theory to explain a particular phenomenon. But these extra fields are, to the best of my understanding, not grafted on to explain such delocalization; they’re the actual basic content of the modified gravity theories and necessary to obtain a workable theory at all. MOND by itself, after all, is not a theory of gravity; the problem then is making one compatible with it, and every actual attempt at that that I’m aware of involves these extra fields, again, not as an epicycle for the bullet cluster, but as a way of constructing a workable theory at all. So, I don’t think that comparison is apt here.
One could perhaps say that such theories are epicycles upon MOND—since the timeline may go MOND, then bullet cluster, then proper modified gravity theories—but for the reasons above I don’t think that makes a lot of sense either.
If this was some post-hoc epicycle then your comment would make some sense; but as it is, I don’t think it does. Is there some reason that I’m missing that it should be regarded as a post-hoc epicycle?
Note that Hossenfelder herself says modified gravity is probably not correct! It’s still important to understand what is or is not a valid argument against it. The other arguments for dark matter sure seem pretty compelling!
(Also, uh, I don’t think “People who think X are just closed-minded and clearly not open to persuasion” is generally not the sort of charity we try to go for here on LW...? I didn’t downvote you but, like, accusing people of being closed-minded rather than actually arguing is on the path to becoming similarly close-minded oneself, you know?)
Thank you. The multipole moment chart is cited frequently and I was always wondering what it would look like in counterfactual worlds without DM. Therefore I am especially grateful for your explanations:
Can you provide a link to read up further on this? Preferably not a summary but the actual research article.
O! So excited to see this—I haven’t had a chance to more than quickly skim, but will dig in after work tonight. But: what about recent detection of an external field effect??? Chae et al recently found “the EFE is individually detected at 8σ to 11σ [!!] in“golden” galaxies subjected to exceptionally strong external fields, while it is not detected in exceptionally isolated galaxies...”
It seems clear from multiple lines that there IS dark matter, but this also seems like strong evidence for MOND?? DO WE HAVE BOTH????
Their sample size isn’t huge, and they call for more work to increase the confidence: “the EFE is statistically detected at more than 4σ from a blind test of 153 SPARC rotating galaxies, giving a mean value of the external field consistent with an independent estimate from the galaxies’ environments, and we detect a systematic downward trend in the weak gravity part of the radial acceleration relation at the right acceleration predicted by the EFE of the MOND modified gravity,” but even the 4σ results seem pretty compelling, no?
Sabine thinks it’s both.
I was interested in her claim that the Bullet Cluster is evidence against dark matter.