Critiquing Scasper’s Definition of Subjunctive Dependence
Before we get to the main part, a note: this post discusses subjunctive dependence, and assumes the reader has a background in Functional Decision Theory (FDT). For readers who don’t, I recommend this paper by Eliezer Yudkowsky and Nate Soares. I will leave their definition of subjunctive dependence here, because it is so central to this post:
When two physical systems are computing the same function, we will say that their behaviors “subjunctively depend” upon that function.
So, I just finished reading Dissolving Confusion around Functional Decision Theory by Stephen Casper (scasper). In it, Casper explains FDT quite well, and makes some good points, such as FDT not assuming causation can happen backwards in time. However, Casper makes a claim about subjunctive dependence that’s not only wrong, but might add to confusion around FDT:
Suppose that you design some agent who enters an environment with whatever source code you gave it. Then if the agent’s source code is fixed, a predictor could exploit certain statistical correlations without knowing the source code. For example, suppose the predictor used observations of the agent to make probabilistic inferences about its source code. These could even be observations about how the agent acts in other Newcombian situations. Then the predictor could, without knowing what function the agent computes, make better-than-random guesses about its behavior. This falls outside of Yudkowsky and Soares’ definition of subjunctive dependence, but it has the same effect.
To see where Casper goes wrong, let’s look at a clear example. The classic Newcomb’s problem will do, but now, Omega isn’t running a model of your decision procedure, but has observed your one-box/two-box choices on 100 earlier instances of the game—and uses the percentage of times you one-boxed for her prediction. That is, Omega predicts you one-box iff that percentage is greater than 50. Now, in the version where Omega is running a model of your decision procedure, you and Omega’s model are subjunctively dependent on the same function. In our current version, this isn’t the case, as Omega isn’t running such a model; however, Omega’s prediction is based on observations that are causally influenced by your historic choices, made by historic versions of you. Crucially, “current you” and every “historic you” therefore subjunctively depend on your decision procedure. The FDT graph for this version of Newcomb’s problem looks like this:
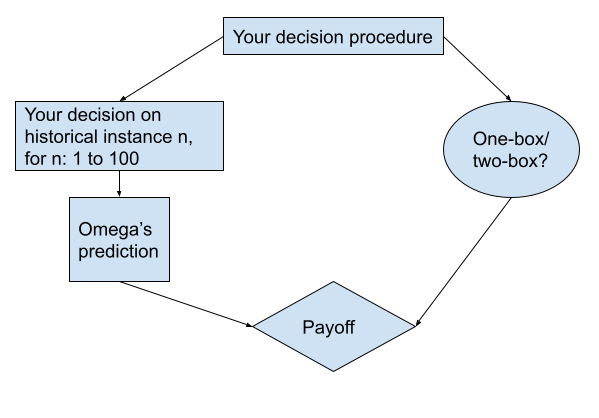
Let’s ask FDT’s question: “Which output of this decision procedure causes the best outcome?”. If it’s two-boxing, your decision procedure causes each historical instance of you to two-box: this causes Omega to predict you two-box. Your decision procedure also causes current you to two-box (the oval box on the right). The payoff, then, is calculated as it is in the classic Newcomb’s problem, and equals $1000.
However, if the answer to the question is one-boxing, then every historical you and current you one-box. Omega predicts you one-box, giving you a payoff of $1,000,000.
Even better, if we assume FDT only faces this kind of Omega (and knows how this Omega operates), FDT can easily exploit Omega by one-boxing >50% of the time and two-boxing in the other cases. That way, Omega will keep predicting you one-box and fill box B. So when one-boxing, you get $1,000,000, but when two-boxing, you get the maximum payoff of $1,001,000. This way, FDT can get an average payoff approaching $1,000,500. I learned this from a conversation with one of the original authors of the FDT paper, Nate Soares (So8res).
So FDT solves the above version of Newcomb’s problem beautifully, and subjunctive dependence is very much in play here. Casper however offers his own definition of subjunctive dependence:
I should consider predictor P to “subjunctively depend” on agent A to the extent that P makes predictions of A’s actions based on correlations that cannot be confounded by my choice of what source code A runs.
I have yet to see a problem of decision theoretic significance that falls within this definition of subjunctive dependence, but outside of Yudkowsky and Soares’ definition. Furthermore, subjunctive dependence isn’t always about predicting future actions, so I object to the use of “predictor” in Casper’s definition. Most importantly, though, note that for a decision procedure to have any effect on the world, something or somebody must be computing (part of) it—so coming up with a Newcomb-like problem where your decision procedure has an effect at two different times/places without Yudkowsky and Soares’ subjunctive dependence being in play seems impossible.
I feel like the notion of “subjunctive dependence” is reversing the direction of causality. It’s not the mathematical function that determines the output of the physical system, it’s the output of the physical system that determines what mathematical function describes it.
Sure, to an extent, reversing the direction of causality is the point, with the hope that it allows solving some tricky decision theoretic problems. But I don’t really see why we’d expect it to be solvable.
Thanks for your reply.
Your brain implements some kind of decision procedure—a mathematical function—that determines what your body does. You decide to lift your left hand, after which your left hand goes up.
Let’s be clear on this: reversing the direction of causality is not the point, and FDT does not use backwards causation in any way. In Newcomb’s Problem, you don’t influence Omega’s model of your decision procedure in any way; you just know that if your decision procedure outputs “one-box”, then Omega’s model of you did so too. This is no different than two identical calculators outputting 4 on 2 + 2, even though there is no causal arrow from one to the other. I plan on doing a whole sequence on FDT, including a post on subjunctive dependence, btw.
If reversing the direction of causality was the point even a little bit, I would not be taking FDT so seriously as I do.
My brain implements a physical computation that determines what my body does. We can make up a bunch of counterfactuals for what this physical computation would have been, had it been given different inputs, and define a mathematical function to be this. However, that mathematical function is determined by the counterfactual outputs, rather than determining the counterfactual outputs.
I don’t follow.
Exactly, a decision procedure. Which is an implementation of a mathematical function, and that’s what FDT is talking about.
I guess to simplify the objection:
A core part of Pearl’s paradigm is how he has defined the way to go from a causal graph to a set of observations of variables. This definition pretty much defines causality, and serves as core for further reasoning about it.
Logical causality lacks the equivalent, a way to go from a causal logical graph to a set of truth values for propositions. I have some basic solution for this problem but they are all much less powerful than what people want out of logical causality. In particular it is trivially solvable if one considers computational causality instead of logical causality.
Most people advocating for logical causality seems to disregard this approach, and instead want to define logical causality purely in terms of logical counterfactuals (whereas usually the Pearlian approach would define counterfactuals in terms of causality). I don’t see the reason to expect this to work.
I guess I have several problems with logical causality/FDT/LDT.
First, there’s a distinction between “efficient algorithm”, “algorithm”, “constructive/intuitionistic function” and “(classical) mathematical function”. Suppose someone tells me to implement a squaring function, so I then write some code for arithmetic, and have a program output some squares. In this case, one can sooort of say that the mathematical function of “squaring” causally influences the output, at least as a fairly accurate abstract approximation. But I wouldn’t be able to implement the vast majority of mathematical functions, so it is a pretty questionable frame. As you go further down the hierarchy towards “efficient algorithm”, it becomes more viable to implement, as issues such as “this function cannot be defined with any finite amount of information” or “I cannot think of any algorithm to implement this function” dissipate. I have much less problem with notions like “computational causality” (or alternatively a sort of logical-semantic causality that I’ve come up with a definition for which I’ve been thinking of whether to write a LW post about, leaning towards no because LDT-type stuff seems like a dead end).
However, even insofar as we grant the above process as implying a logical causality, I wasn’t created by this sort of process. I was created by some complicated history involving e.g. evolution. This complicated history doesn’t have any position where one could point to a mathematical function that was taken and implemented; instead evolution is a continuous optimization process working against a changing reality.
Finally, even if all of these problems were solved, the goal with logical causality is often not just to cover structurally identical decision procedures, but also logically “isomorphic” things, for an extremely broad definition of “isomorphic” covering e.g. “proof searches about X” as well as X itself. But computationally, proof searches are very distinct from from the objects they are reasoning about.
Thanks for this post, I think it has high clarificational value and that your interpretation is valid and good. In my post, I failed to cite Y&S’s actual definition and should have been more careful. I ended up critiquing a definition that probably resembled MacAskill’s definition more than Y&S’s, and it seems to have been somewhat of an accidental strawperson. In fairness to me though, Y&S never offered any example with the minimal conditions for SD to apply in their original paper while I did. This is part of what led to MacAskill’s counterpost.
This all said, I do think there is something that my definition offers (clarifies?) that Y&S’s does not. Consider your example. Suppose I have played 100 Newcombian games and one-boxed each time. Your Omega will then predict that on the 101st, I’ll one-box again. If I make decisions independently each time I play the game, then we have the example you presented and which I agree with. But I think it’s more interesting if I am allowed to change my strategy. From my perspective as an agent trying to counfound Omega and win, I should not consider Omega’s predictions and my actions to subjuntively depend, and my definition would say so. Under the definition from Y&S, I think it’s less clear in this situation what I should think. Should say that we’re SD “so far”? Probably not. Should I wait until I finish all interaction with Omega and then decide whether or not we were SD in retrospect? Seems silly. So I think my definition may lead to a more practical understanding than Y&S’s.
Do you think we’re about on the same page? Thanks again for the post.
Thanks for your reply!
I think your definition does say so, and rightfully so. Your source code is run in the historical cases as well, so indirectly it does confound Omega. Or are you saying your source code changes? Then there’s no (or no full) subjunctive dependence with either definition. If your source code remains the same but your specific-for-each-game strategy changes, we can imagine something like using historical data as an observation in your strategy, in which case it can be different each time. But again, then there is no (or no full) subjunctive dependence with either definition. I might misunderstand what you mean though.
Thanks again for your reply, I think discussing this is important!