Fermi Estimates
Just before the Trinity test, Enrico Fermi decided he wanted a rough estimate of the blast’s power before the diagnostic data came in. So he dropped some pieces of paper from his hand as the blast wave passed him, and used this to estimate that the blast was equivalent to 10 kilotons of TNT. His guess was remarkably accurate for having so little data: the true answer turned out to be 20 kilotons of TNT.
Fermi had a knack for making roughly-accurate estimates with very little data, and therefore such an estimate is known today as a Fermi estimate.
Why bother with Fermi estimates, if your estimates are likely to be off by a factor of 2 or even 10? Often, getting an estimate within a factor of 10 or 20 is enough to make a decision. So Fermi estimates can save you a lot of time, especially as you gain more practice at making them.
Estimation tips
These first two sections are adapted from Guestimation 2.0.
Dare to be imprecise. Round things off enough to do the calculations in your head. I call this the spherical cow principle, after a joke about how physicists oversimplify things to make calculations feasible:
Milk production at a dairy farm was low, so the farmer asked a local university for help. A multidisciplinary team of professors was assembled, headed by a theoretical physicist. After two weeks of observation and analysis, the physicist told the farmer, “I have the solution, but it only works in the case of spherical cows in a vacuum.”
By the spherical cow principle, there are 300 days in a year, people are six feet (or 2 meters) tall, the circumference of the Earth is 20,000 mi (or 40,000 km), and cows are spheres of meat and bone 4 feet (or 1 meter) in diameter.
Decompose the problem. Sometimes you can give an estimate in one step, within a factor of 10. (How much does a new compact car cost? $20,000.) But in most cases, you’ll need to break the problem into several pieces, estimate each of them, and then recombine them. I’ll give several examples below.
Estimate by bounding. Sometimes it is easier to give lower and upper bounds than to give a point estimate. How much time per day does the average 15-year-old watch TV? I don’t spend any time with 15-year-olds, so I haven’t a clue. It could be 30 minutes, or 3 hours, or 5 hours, but I’m pretty confident it’s more than 2 minutes and less than 7 hours (400 minutes, by the spherical cow principle).
Can we convert those bounds into an estimate? You bet. But we don’t do it by taking the average. That would give us (2 mins + 400 mins)/2 = 201 mins, which is within a factor of 2 from our upper bound, but a factor 100 greater than our lower bound. Since our goal is to estimate the answer within a factor of 10, we’ll probably be way off.
Instead, we take the geometric mean — the square root of the product of our upper and lower bounds. But square roots often require a calculator, so instead we’ll take the approximate geometric mean (AGM). To do that, we average the coefficients and exponents of our upper and lower bounds.
So what is the AGM of 2 and 400? Well, 2 is 2×100, and 400 is 4×102. The average of the coefficients (2 and 4) is 3; the average of the exponents (0 and 2) is 1. So, the AGM of 2 and 400 is 3×101, or 30. The precise geometric mean of 2 and 400 turns out to be 28.28. Not bad.
What if the sum of the exponents is an odd number? Then we round the resulting exponent down, and multiply the final answer by three. So suppose my lower and upper bounds for how much TV the average 15-year-old watches had been 20 mins and 400 mins. Now we calculate the AGM like this: 20 is 2×101, and 400 is still 4×102. The average of the coefficients (2 and 4) is 3; the average of the exponents (1 and 2) is 1.5. So we round the exponent down to 1, and we multiple the final result by three: 3(3×101) = 90 mins. The precise geometric mean of 20 and 400 is 89.44. Again, not bad.
Sanity-check your answer. You should always sanity-check your final estimate by comparing it to some reasonable analogue. You’ll see examples of this below.
Use Google as needed. You can often quickly find the exact quantity you’re trying to estimate on Google, or at least some piece of the problem. In those cases, it’s probably not worth trying to estimate it without Google.
Fermi estimation failure modes
Fermi estimates go wrong in one of three ways.
First, we might badly overestimate or underestimate a quantity. Decomposing the problem, estimating from bounds, and looking up particular pieces on Google should protect against this. Overestimates and underestimates for the different pieces of a problem should roughly cancel out, especially when there are many pieces.
Second, we might model the problem incorrectly. If you estimate teenage deaths per year on the assumption that most teenage deaths are from suicide, your estimate will probably be way off, because most teenage deaths are caused by accidents. To avoid this, try to decompose each Fermi problem by using a model you’re fairly confident of, even if it means you need to use more pieces or give wider bounds when estimating each quantity.
Finally, we might choose a nonlinear problem. Normally, we assume that if one object can get some result, then two objects will get twice the result. Unfortunately, this doesn’t hold true for nonlinear problems. If one motorcycle on a highway can transport a person at 60 miles per hour, then 30 motorcycles can transport 30 people at 60 miles per hour. However, 104 motorcycles cannot transport 104 people at 60 miles per hour, because there will be a huge traffic jam on the highway. This problem is difficult to avoid, but with practice you will get better at recognizing when you’re facing a nonlinear problem.
Fermi practice
When getting started with Fermi practice, I recommend estimating quantities that you can easily look up later, so that you can see how accurate your Fermi estimates tend to be. Don’t look up the answer before constructing your estimates, though! Alternatively, you might allow yourself to look up particular pieces of the problem — e.g. the number of Sikhs in the world, the formula for escape velocity, or the gross world product — but not the final quantity you’re trying to estimate.
Most books about Fermi estimates are filled with examples done by Fermi estimate experts, and in many cases the estimates were probably adjusted after the author looked up the true answers. This post is different. My examples below are estimates I made before looking up the answer online, so you can get a realistic picture of how this works from someone who isn’t “cheating.” Also, there will be no selection effect: I’m going to do four Fermi estimates for this post, and I’m not going to throw out my estimates if they are way off. Finally, I’m not all that practiced doing “Fermis” myself, so you’ll get to see what it’s like for a relative newbie to go through the process. In short, I hope to give you a realistic picture of what it’s like to do Fermi practice when you’re just getting started.
Example 1: How many new passenger cars are sold each year in the USA?

As with all Fermi problems, there are many different models we could build. For example, we could estimate how many new cars a dealership sells per month, and then we could estimate how many dealerships there are in the USA. Or we could try to estimate the annual demand for new cars from the country’s population. Or, if we happened to have read how many Toyota Corollas were sold last year, we could try to build our estimate from there.
The second model looks more robust to me than the first, since I know roughly how many Americans there are, but I have no idea how many new-car dealerships there are. Still, let’s try it both ways. (I don’t happen to know how many new Corollas were sold last year.)
Approach #1: Car dealerships
How many new cars does a dealership sell per month, on average? Oofta, I dunno. To support the dealership’s existence, I assume it has to be at least 5. But it’s probably not more than 50, since most dealerships are in small towns that don’t get much action. To get my point estimate, I’ll take the AGM of 5 and 50. 5 is 5×100, and 50 is 5×101. Our exponents sum to an odd number, so I’ll round the exponent down to 0 and multiple the final answer by 3. So, my estimate of how many new cars a new-car dealership sells per month is 3(5×100) = 15.
Now, how many new-car dealerships are there in the USA? This could be tough. I know several towns of only 10,000 people that have 3 or more new-car dealerships. I don’t recall towns much smaller than that having new-car dealerships, so let’s exclude them. How many cities of 10,000 people or more are there in the USA? I have no idea. So let’s decompose this problem a bit more.
How many counties are there in the USA? I remember seeing a map of counties colored by which national ancestry was dominant in that county. (Germany was the most common.) Thinking of that map, there were definitely more than 300 counties on it, and definitely less than 20,000. What’s the AGM of 300 and 20,000? Well, 300 is 3×102, and 20,000 is 2×104. The average of coefficients 3 and 2 is 2.5, and the average of exponents 2 and 4 is 3. So the AGM of 300 and 20,000 is 2.5×103 = 2500.
Now, how many towns of 10,000 people or more are there per county? I’m pretty sure the average must be larger than 10 and smaller than 5000. The AGM of 10 and 5000 is 300. (I won’t include this calculation in the text anymore; you know how to do it.)
Finally, how many car dealerships are there in cities of 10,000 or more people, on average? Most such towns are pretty small, and probably have 2-6 car dealerships. The largest cities will have many more: maybe 100-ish. So I’m pretty sure the average number of car dealerships in cities of 10,000 or more people must be between 2 and 30. The AGM of 2 and 30 is 7.5.
Now I just multiply my estimates:
[15 new cars sold per month per dealership] × [12 months per year] × [7.5 new-car dealerships per city of 10,000 or more people] × [300 cities of 10,000 or more people per county] × [2500 counties in the USA] = 1,012,500,000.
A sanity check immediately invalidates this answer. There’s no way that 300 million American citizens buy a billion new cars per year. I suppose they might buy 100 million new cars per year, which would be within a factor of 10 of my estimate, but I doubt it.
As I suspected, my first approach was problematic. Let’s try the second approach, starting from the population of the USA.
Approach #2: Population of the USA
There are about 300 million Americans. How many of them own a car? Maybe 1⁄3 of them, since children don’t own cars, many people in cities don’t own cars, and many households share a car or two between the adults in the household.
Of the 100 million people who own a car, how many of them bought a new car in the past 5 years? Probably less than half; most people buy used cars, right? So maybe 1⁄4 of car owners bought a new car in the past 5 years, which means 1 in 20 car owners bought a new car in the past year.
100 million / 20 = 5 million new cars sold each year in the USA. That doesn’t seem crazy, though perhaps a bit low. I’ll take this as my estimate.
Now is your last chance to try this one on your own; in the next paragraph I’ll reveal the true answer.
…
…
...
Now, I Google new cars sold per year in the USA. Wikipedia is the first result, and it says “In the year 2009, about 5.5 million new passenger cars were sold in the United States according to the U.S. Department of Transportation.”
Boo-yah!
Example 2: How many fatalities from passenger-jet crashes have there been in the past 20 years?

As far as I can tell, passenger-jet crashes (with fatalities) almost always make it on the TV news and (more relevant to me) the front page of Google News. Exciting footage and multiple deaths will do that. So working just from memory, it feels to me like there are about 5 passenger-jet crashes (with fatalities) per year, so maybe there were about 100 passenger jet crashes with fatalities in the past 20 years.
Now, how many fatalities per crash? From memory, it seems like there are usually two kinds of crashes: ones where everybody dies (meaning: about 200 people?), and ones where only about 10 people die. I think the “everybody dead” crashes are less common, maybe 1⁄4 as common. So the average crash with fatalities should cause (200×1/4)+(10×3/4) = 50+7.5 = 60, by the spherical cow principle.
60 fatalities per crash × 100 crashes with fatalities over the past 20 years = 6000 passenger fatalities from passenger-jet crashes in the past 20 years.
Last chance to try this one on your own...
…
…
…
A Google search again brings me to Wikipedia, which reveals that an organization called ACRO records the number of airline fatalities each year. Unfortunately for my purposes, they include fatalities from cargo flights. After more Googling, I tracked down Boeing’s “Statistical Summary of Commercial Jet Airplane Accidents, 1959-2011,” but that report excludes jets lighter than 60,000 pounds, and excludes crashes caused by hijacking or terrorism.
It appears it would be a major research project to figure out the true answer to our question, but let’s at least estimate it from the ACRO data. Luckily, ACRO has statistics on which percentage of accidents are from passenger and other kinds of flights, which I’ll take as a proxy for which percentage of fatalities are from different kinds of flights. According to that page, 35.41% of accidents are from “regular schedule” flights, 7.75% of accidents are from “private” flights, 5.1% of accidents are from “charter” flights, and 4.02% of accidents are from “executive” flights. I think that captures what I had in mind as “passenger-jet flights.” So we’ll guess that 52.28% of fatalities are from “passenger-jet flights.” I won’t round this to 50% because we’re not doing a Fermi estimate right now; we’re trying to check a Fermi estimate.
According to ACRO’s archives, there were 794 fatalities in 2012, 828 fatalities in 2011, and… well, from 1993-2012 there were a total of 28,021 fatalities. And 52.28% of that number is 14,649.
So my estimate of 6000 was off by less than a factor of 3!
Example 3: How much does the New York state government spends on K-12 education every year?

How many people live in New York? I seem to recall that NYC’s greater metropolitan area is about 20 million people. That’s probably most of the state’s population, so I’ll guess the total is about 30 million.
How many of those 30 million people attend K-12 public schools? I can’t remember what the United States’ population pyramid looks like, but I’ll guess that about 1⁄6 of Americans (and hopefully New Yorkers) attend K-12 at any given time. So that’s 5 million kids in K-12 in New York. The number attending private schools probably isn’t large enough to matter for factor-of-10 estimates.
How much does a year of K-12 education cost for one child? Well, I’ve heard teachers don’t get paid much, so after benefits and taxes and so on I’m guessing a teacher costs about $70,000 per year. How big are class sizes these days, 30 kids? By the spherical cow principle, that’s about $2,000 per child, per year on teachers’ salaries. But there are lots of other expenses: buildings, transport, materials, support staff, etc. And maybe some money goes to private schools or other organizations. Rather than estimate all those things, I’m just going to guess that about $10,000 is spent per child, per year.
If that’s right, then New York spends $50 billion per year on K-12 education.
Last chance to make your own estimate!
…
…
…
Before I did the Fermi estimate, I had Julia Galef check Google to find this statistic, but she didn’t give me any hints about the number. Her two sources were Wolfram Alpha and a web chat with New York’s Deputy Secretary for Education, both of which put the figure at approximately $53 billion.
Which is definitely within a factor of 10 from $50 billion. :)
Example 4: How many plays of My Bloody Valentine’s “Only Shallow” have been reported to last.fm?

My Fermi problem is: How many plays of “Only Shallow” have been reported to last.fm?
My Bloody Valentine is a popular “indie” rock band, and “Only Shallow” is probably one of their most popular tracks. How can I estimate how many plays it has gotten on last.fm?
What do I know that might help?
I know last.fm is popular, but I don’t have a sense of whether they have 1 million users, 10 million users, or 100 million users.
I accidentally saw on Last.fm’s Wikipedia page that just over 50 billion track plays have been recorded. We’ll consider that to be one piece of data I looked up to help with my estimate.
I seem to recall reading that major music services like iTunes and Spotify have about 10 million tracks. Since last.fm records songs that people play from their private collections, whether or not they exist in popular databases, I’d guess that the total number of different tracks named in last.fm’s database is an order of magnitude larger, for about 100 million tracks named in its database.
I would guess that track plays obey a power law, with the most popular tracks getting vastly more plays than tracks of average popularity. I’d also guess that there are maybe 10,000 tracks more popular than “Only Shallow.”
Next, I simulated being good at math by having Qiaochu Yuan show me how to do the calculation. I also allowed myself to use a calculator. Here’s what we do:
Plays(rank) = C/(rankP)
P is the exponent for the power law, and C is the proportionality constant. We’ll guess that P is 1, a common power law exponent for empirical data. And we calculate C like so:
C ≈ [total plays]/ln(total songs) ≈ 2.5 billion
So now, assuming the song’s rank is 10,000, we have:
Plays(104) = 2.5×109/(104)
Plays(“Only Shallow”) = 250,000
That seems high, but let’s roll with it. Last chance to make your own estimate!
…
…
...
And when I check the answer, I see that “Only Shallow” has about 2 million plays on last.fm.
My answer was off by less than a factor of 10, which for a Fermi estimate is called victory!
Unfortunately, last.fm doesn’t publish all-time track rankings or other data that might help me to determine which parts of my model were correct and incorrect.
Further examples
I focused on examples that are similar in structure to the kinds of quantities that entrepreneurs and CEOs might want to estimate, but of course there are all kinds of things one can estimate this way. Here’s a sampling of Fermi problems featured in various books and websites on the subject:
Play Fermi Questions: 2100 Fermi problems and counting.
Guesstimation (2008): If all the humans in the world were crammed together, how much area would we require? What would be the mass of all 108 MongaMillions lottery tickets? On average, how many people are airborne over the US at any given moment? How many cells are there in the human body? How many people in the world are picking their nose right now? What are the relative costs of fuel for NYC rickshaws and automobiles?
Guesstimation 2.0 (2011): If we launched a trillion one-dollar bills into the atmosphere, what fraction of sunlight hitting the Earth could we block with those dollar bills? If a million monkeys typed randomly on a million typewriters for a year, what is the longest string of consecutive correct letters of *The Cat in the Hat (starting from the beginning) would they likely type? How much energy does it take to crack a nut? If an airline asked its passengers to urinate before boarding the airplane, how much fuel would the airline save per flight? What is the radius of the largest rocky sphere from which we can reach escape velocity by jumping?
How Many Licks? (2009): What fraction of Earth’s volume would a mole of hot, sticky, chocolate-jelly doughnuts be? How many miles does a person walk in a lifetime? How many times can you outline the continental US in shoelaces? How long would it take to read every book in the library? How long can you shower and still make it more environmentally friendly than taking a bath?
Ballparking (2012): How many bolts are in the floor of the Boston Garden basketball court? How many lanes would you need for the outermost lane of a running track to be the length of a marathon? How hard would you have to hit a baseball for it to never land?
University of Maryland Fermi Problems Site: How many sheets of letter-sized paper are used by all students at the University of Maryland in one semester? How many blades of grass are in the lawn of a typical suburban house in the summer? How many golf balls can be fit into a typical suitcase?
Stupid Calculations: a blog of silly-topic Fermi estimates.
Conclusion
Fermi estimates can help you become more efficient in your day-to-day life, and give you increased confidence in the decisions you face. If you want to become proficient in making Fermi estimates, I recommend practicing them 30 minutes per day for three months. In that time, you should be able to make about (2 Fermis per day)×(90 days) = 180 Fermi estimates.
If you’d like to write down your estimation attempts and then publish them here, please do so as a reply to this comment. One Fermi estimate per comment, please!
Alternatively, post your Fermi estimates to the dedicated subreddit.
Update 03/06/2017: I keep getting requests from professors to use this in their classes, so: I license anyone to use this article noncommercially, so long as its authorship is noted (me = Luke Muehlhauser).
- Five Ways To Prioritize Better by (27 Jun 2020 18:40 UTC; 137 points)
- Nuclear risk research ideas: Summary & introduction by (EA Forum; 8 Apr 2022 11:17 UTC; 103 points)
- Relevance Norms; Or, Gricean Implicature Queers the Decoupling/Contextualizing Binary by (22 Nov 2019 6:18 UTC; 102 points)
- The role of tribes in achieving lasting impact and how to create them by (EA Forum; 29 Sep 2021 20:48 UTC; 72 points)
- The Estimation Game: a monthly Fermi estimation web app by (EA Forum; 20 Feb 2023 11:22 UTC; 69 points)
- Guesstimate: An app for making decisions with confidence (intervals) by (EA Forum; 30 Dec 2015 17:30 UTC; 63 points)
- Five Ways To Prioritize Better by (EA Forum; 27 Jun 2020 18:40 UTC; 61 points)
- 's comment on New applied rationality workshops (April, May, and July) by (8 Apr 2013 21:41 UTC; 40 points)
- Nick Bostrom: An Introduction [early draft] by (EA Forum; 31 Jul 2021 17:04 UTC; 38 points)
- Graphical Assumption Modeling by (3 Jan 2015 20:22 UTC; 32 points)
- Celebrating All Who Are in Effective Altruism by (20 Jan 2016 1:31 UTC; 25 points)
- Willing gamblers, spherical cows, and AIs by (8 Apr 2013 21:30 UTC; 25 points)
- The Estimation Game: a monthly Fermi estimation web app by (20 Feb 2023 11:33 UTC; 20 points)
- The Value of Those in Effective Altruism by (17 Feb 2016 0:59 UTC; 18 points)
- 's comment on Rationality Quotes May 2013 by (13 May 2013 0:47 UTC; 17 points)
- 's comment on Lizka’s Quick takes by (EA Forum; 11 Dec 2021 20:46 UTC; 16 points)
- Fermi Estimate by (EA Forum; 20 Jun 2022 23:00 UTC; 15 points)
- The role of tribes in achieving lasting impact and how to create them by (29 Sep 2021 20:48 UTC; 14 points)
- Research project idea: Impact assessment of nuclear-risk-related orgs, programmes, movements, etc. by (EA Forum; 15 Apr 2023 14:39 UTC; 13 points)
- Lifetime Impact of a GiveWell Researcher? by (EA Forum; 16 Aug 2021 23:26 UTC; 11 points)
- 's comment on [LINK] How to calibrate your confidence intervals by (25 Apr 2013 9:03 UTC; 11 points)
- The Value of Those in Effective Altruism by (EA Forum; 17 Feb 2016 0:54 UTC; 8 points)
- 's comment on Minor, perspective changing facts by (22 Apr 2013 20:01 UTC; 8 points)
- Consider Applying to Organize an EAGx Event, And An Offer To Help Apply by (EA Forum; 22 Jan 2016 20:14 UTC; 6 points)
- 's comment on How likely is a nuclear exchange between the US and Russia? by (EA Forum; 4 May 2021 13:45 UTC; 5 points)
- Meetup : London Practical—Sunday 7th July by (26 Jun 2013 9:05 UTC; 5 points)
- 's comment on How to Evaluate Data? by (9 Apr 2013 19:25 UTC; 5 points)
- 's comment on Purchasing research effectively open thread by (24 Jan 2015 10:40 UTC; 5 points)
- Research Summary: Forecasting with Large Language Models by (EA Forum; 2 Apr 2023 10:52 UTC; 4 points)
- 's comment on [Link] A rational response to the Paris attacks and ISIS by (24 Nov 2015 21:42 UTC; 3 points)
- 's comment on Graphical Assumption Modeling by (3 Jan 2015 21:10 UTC; 3 points)
- Meetup : Washington, D.C.: Fermi Estimates by (2 Feb 2016 21:14 UTC; 3 points)
- Meetup : Washington, D.C.: Fermi Estimates by (8 Jul 2015 18:15 UTC; 3 points)
- Measuring QALYs from advocating a rational response to the Paris attacks and ISIS by (EA Forum; 23 Nov 2015 17:37 UTC; 2 points)
- What are some responsibility bundle bargains for medium-sized enterprises? by (EA Forum; 10 Jan 2022 19:38 UTC; 2 points)
- Meetup : Washington, D.C.: Fermi Estimates by (22 Jun 2016 1:13 UTC; 2 points)
- 's comment on Failed Utopia #4-2 by (31 May 2013 8:57 UTC; 2 points)
- 's comment on The Value of Those in Effective Altruism by (4 May 2016 23:14 UTC; 2 points)
- 's comment on Hi, I’m Holden Karnofsky. AMA about jobs at Open Philanthropy by (EA Forum; 28 Mar 2018 15:50 UTC; 1 point)
- 's comment on Systematically under explored project areas? by (EA Forum; 6 Oct 2015 21:03 UTC; 1 point)
- Stime di Fermi by (EA Forum; 31 Dec 2022 3:38 UTC; 1 point)
- フェルミ推定 + 適用例 by (EA Forum; 19 Jul 2023 15:33 UTC; 1 point)
- Meetup : Brussels—Calibration and other games by (26 Feb 2014 16:33 UTC; 1 point)
- A proposed inefficiency in the Bitcoin markets by (27 Dec 2013 3:48 UTC; 1 point)
- 's comment on Hi, I’m Holden Karnofsky. AMA about jobs at Open Philanthropy by (EA Forum; 26 Apr 2018 5:08 UTC; 0 points)
- 's comment on Emotional tools for the beginner rationalist by (11 Oct 2015 17:13 UTC; 0 points)
Correction:
(2 Fermis per day)×(90 days) = 200 Fermi estimates.
2 fermis a day x 3000 days = 6000 fermi estimates
It’s probably worth figuring out what went wrong in Approach 1 to Example 1, which I think is this part:
Note that this gives 750,000 cities of 10,000 or more people in the US, for a total of at least 7.5 billion people in the US. So it’s already clearly wrong here. I’d say 300 cities of 10,000 people or more per county is way too high; I’d put it at more like 1 (Edit: note that this gives at least 250 million people in the US and that’s about right). This brings down the final estimate from this approach by a factor of 300, or down to 3 million, which is much closer.
(Verification: I just picked a random US state and a random county in it from Wikipedia and got Bartow County, Georgia, which has a population of 100,000. That means it has at most 10 cities with 10,000 or more people, and going through the list of cities it actually looks like it only has one such city.)
This gives about 2,500 cities in the US total with population 10,000 or more. I can’t verify this number, but according to Wikipedia there are about 300 cities in the US with population 100,000 or more. Assuming the populations of cities are power-law distributed with exponent 1, this means that the nth-ranked city has population about 30,000,000/n, so this gives about 3,000 cities in the US with population 10,000 or more.
And in fact we didn’t even need to use Wikipedia! Just assuming that the population of cities is power-law distributed with exponent 1, we see that the distribution is determined by the population of the most populous city. Let’s take this to be 20 million people (the number you used for New York City). Then the nth-ranked city in the US has population about 20,000,000/n, so there are about 2,000 cities with population 10,000 or more.
Edit: Found the actual number. According to the U.S. Census Bureau, as of 2008, the actual number is about 2,900 cities.
Incidentally, this shows another use of Fermi estimates: if you get one that’s obviously wrong, you’ve discovered an opportunity to fix some aspect of your model of the world.
I feel compelled to repeat this old physics classic:
:-)
That is beautiful.
I’ve run meetups on this topic twice now. Every time I do, it’s difficult to convince people it’s a useful skill. More words about when estimation is useful would be nice.
In most exercises that you can find on Fermi calculations, you can also actually find the right answer, written down somewhere online. And, well, being able to quickly find information is probably a more useful skill to practice than estimation; because it works for non-quantified information too. I understand why this is; you want to be able to show that these estimates aren’t very far off, and for that you need to be able to find the actual numbers somehow. But that means that your examples don’t actually motivate the effort of practicing, they only demonstrate how.
I suspect the following kinds of situations are fruitful for estimation:
Deciding in unfamiliar situations, because you don’t know how things will turn out for you. If you’re in a really novel situation, you can’t even find out how the same decision has worked for other people before, and so you have to guess at expected value using the best information that you can find.
Value of information calculations, like here and here, where you cannot possibly know the expected value of things, because you’re trying to decide if you should pay for information about their value.
Deciding when you’re not online, because this makes accessing information more expensive than computation.
Decisions where you have unusual information for a particular situation—the internet might have excellent base-rate information about your general situation, but it’s unlikely to give you the precise odds so that you can incorporate the extra information that you have in this specific situation.
Looking smart. It’s nice to look smart sometimes.
Others? Does anyone have examples of when Fermi calculations helped them make a decision?
Fermi’s seem essential for business to me. Others agree; they’re taught in standard MBA programs. For example:
Can our business (or our non-profit) afford to hire an extra person right now? E.g., if they require the same training time before usefulness that others required, will they bring in more revenue in time to make up for the loss of runway?
If it turns out that product X is a success, how much money might it make—is it enough to justify investigating the market?
Is it cheaper (given the cost of time) to use disposable dishes or to wash the dishes?
Is it better to process payments via paypal or checks, given the fees involved in paypal vs. the delays, hassles, and associated risks of non-payment involved in checks?
And on and on. I use them several times a day for CFAR and they seem essential there.
They’re useful also for one’s own practical life: commute time vs. rent tradeoffs; visualizing “do I want to have a kid? how would the time and dollar cost actually impact me?”, realizing that macademia nuts are actually a cheap food and not an expensive food (once I think “per calorie” and not “per apparent size of the container”), and so on and so on.
Oh, right! I actually did the comute time vs. rent computation when I moved four months ago! And wound up with a surprising enough number that I thought about it very closely, and decided that number was about right, and changed how I was looking for apartments. How did I forget that?
Thanks!
But calories aren’t the only thing you care about—the ability to satiate you also matters. (Seed oil is even cheaper per calorie.)
The main use I put Fermi estimates to is fact-checking: when I see a statistic quoted, I would like to know if it is reasonable (especially if I suspect that it has been misquoted somehow).
Qiaochu adds:
I also think Fermi calculations are just fun. It makes me feel totally awesome to be able to conjure approximate answers to questions out of thin air.
There’s a free book on this sort of thing, under a Creative Commons license, called Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving. Among the fun things in it:
Chapter 1: Using dimensional analysis to quickly pull correct-ish equations out of thin air!
Chapter 2: Focusing on easy cases. It’s amazing how many problems become simpler when you set some variables equal to 1, 0, or ∞.
Chapter 3: An awful lot of things look like rectangles if you squint at them hard enough. Rectangles are nice.
Chapter 4: Drawing pictures can help. Humans are good at looking at shapes.
Chapter 5: Approximate arithmetic in which all numbers are either 1, a power of 10, or “a few”—roughly 3, which is close to the geometric mean of 1 and 10. A few times a few is ten, for small values of “is”. Multiply and divide large numbers on your fingers!
… And there’s some more stuff, too, and some more chapters, but that’ll do for an approximate summary.
XKCD’s What If? has some examples of Fermi calculations, for instance at the start of working out the effects of “a mole of moles” (similar to a mole of choc donuts, which is what reminded me).
Thanks, Luke, this was helpful!
There is a sub-technique that could have helped you get a better answer for the first approach to example 1: perform a sanity check not only on the final value, but on any intermediate value you can think of.
In this example, when you estimated that there are 2500 counties, and that the average county has 300 towns with population greater than 10,000, that implies a lower bound for the total population of the US: assuming that all towns have exactly 10,000 people, that gets you a US population of 2,500x300x10,000=7,500,000,000! That’s 7.5 billion people. Of course, in real life, some people live in smaller towns, and some towns have more then 10,000 people, which makes the true implied estimate even larger.
At this point you know that either your estimate for number of counties, or your estimate for number of towns with population above 10,000 per county, or both, must decrease to get an implied population of about 300 million. This would have brought your overall estimate down to within a factor of 10.
I had the pleasure the other day of trying my hand on a slightly unusual use of Fermi estimates: trying to guess whether something unlikely has ever happened. In particular, the question was “Has anyone ever been killed by a falling piano as in the cartoon trope?” Others nearby at the time objected, “but you don’t know anything about this!” which I found amusing because of course I know quite a lot about pianos, things falling, how people can be killed by things falling, etc. so how could I possibly not know anything about pianos falling and killing people? Unfortunately, our estimate gave it at around 1-10 deaths by piano-falling so we weren’t able to make a strong conclusion either way over whether this happened. I would be interested to hear if anyone got a significantly different result. (We only considered falling grands or baby grands to count as upright pianos, keyboards, etc. just aren’t humorous enough for the cartoon trope.)
I’ll try. Let’s see, grands and baby grands date back to something like the 1700s; I’m sure I’ve heard of Mozart or Beethoven using pianos, so that gives me a time-window of 300 years for falling pianos to kill people in Europe or America.
What were their total population? Well, Europe+America right now is, I think, something like 700m people; I’d guess back in the 1700s, it was more like… 50m feels like a decent guess. How many people in total? A decent approximation to exponential population growth is to simply use the average of 700m and 50m, which is 325, times 300 years, 112500m person-years, and a lifespan of 70 years, so 1607m persons over those 300 years.
How many people have pianos? Visiting families, I rarely see pianos; maybe 1 in 10 had a piano at any point. If families average a size of 4 and 1 in 10 families has a piano, then we convert our total population number to, (1607m / 4) / 10, 40m pianos over that entire period.
But wait, this is for falling pianos, not all pianos; presumably a falling piano must be at least on a second story. If it simply crushes a mover’s foot while on the porch, that’s not very comedic at all. We want genuine verticality, real free fall. So our piano must be on a second or higher story. Why would anyone put a piano, baby or grand, that high? Unless they had to, that is—because they live in a city where they can’t afford a ground-level apartment or house.
So we’ll ask instead for urban families with pianos, on a second or higher story. The current urban percentage of the population is hitting majority (50%) in some countries, but in the 1700s it would’ve been close to 0%. Average again: 50+0/2=25%, so we cut 40m by 75% to 30m. Every building has a ground floor, but not every building has more than 1 floor, so some urban families will be able to live on the ground floor and put their piano there and not fear a humorously musical death from above. I’d guess (and here I have no good figures to justify it) that the average urban building over time has closer to an average of 2 floors than more or less, since structural steel is so recent, so we’ll cut 30m to 15m.
So, there were 15m families in urban areas on non-ground-floors with pianos. And how would pianos get to non-ground-floors...? By lifting, of course, on cranes and things. (Yes, even in the 1700s. One aspect of Amsterdam that struck me when I was visiting in 2005 was that each of the narrow building fronts had big hooks at their peaks; I was told this was for hoisting things up. Like pianos, I shouldn’t wonder.) Each piano has to be lifted up, and, sad to say, taken down at some point. Even pianos don’t live forever. So that’s 30m hoistings and lowerings, each of which could be hilariously fatal, an average of 0.1m a year.
How do we go from 30m crane operations to how many times a piano falls and then also kills someone? A piano is seriously heavy, so one would expect the failure rate to be nontrivial, but at the same time, the crews ought to know this and be experienced at moving heavy stuff; offhand, I’ve never heard of falling pianos.
At this point I cheated and look at the OSHA workplace fatalities data: 4609 for 2011. At a guess, half the USA population is gainfully employed, so 4700 out of 150m died. Let’s assume that ‘piano moving’ is not nearly as risky as it sounds and merely has the average American risk of dying on the job.
We have 100000 piano hoistings a year, per previous. If a team of 3 can do lifts or hoisting of pianos a day, then we need 136 teams or 410 people. How many of these 410 will die each year, times 300?
(410 * (4700/150000000))*300 = 3.9So irritatingly, I’m not that sure that I can show that anyone has died by falling piano, even though I really expect that people have. Time to check in Google.
Searching for
killed by falling piano, I see:a joke
two possibles
one man killed by it falling out of a truck onto him
one kid killed by a piano in a dark alley
But no actual cases of pianos falling a story onto someone. So, the calculation may be right − 0 is within an order of magnitude of 3.9, after all.
No it’s not! Actually it’s infinitely many orders of magnitude away!
Nitpick alert: I believe pianos used to be a lot more common. There was a time when they were a major source of at-home music. On the other hand, the population was much smaller then, so maybe the effects cancel out.
I wonder. Pianos are still really expensive. They’re very bulky, need skilled maintenance and tuning, use special high-tension wires, and so on. Even if technological progress, outsourcing manufacture to China etc haven’t reduced the real price of pianos, the world is also much wealthier now and more able to afford buying pianos. Another issue is the growth of the piano as the standard Prestigious Instrument for the college arms races (vastly more of the population goes to college now than in 1900) or signaling high culture or modernity (in the case of East Asia); how many pianos do you suppose there are scattered now across the USA compared to 1800? Or in Japan and China and South Korea compared to 1900?
And on the other side, people used to make music at home, yes—but for that there are many cheaper, more portable, more durable alternatives, such as cut-down versions of pianos.
Concert grands, yes, but who has room for one of those? Try selling an old upright piano when clearing a deceased relative’s estate. In the UK, you’re more likely to have to pay someone to take it away, and it will just go to a scrapheap. Of course, that’s present day, and one reason no-one wants an old piano is that you can get a better electronic one new for a few hundred pounds.
But back in Victorian times, as Nancy says elsethread, a piano was a standard feature of a Victorian parlor, and that went further down the social scale that you are imagining, and lasted at least through the first half of the twentieth century. Even better-off working people might have one, though not the factory drudges living in slums. It may have been different in the US though.
Certainly: http://www.nytimes.com/2012/07/30/arts/music/for-more-pianos-last-note-is-thud-in-the-dump.html?_r=2&ref=arts But like diamonds (I have been told that you cannot resell a diamond for anywhere near what you paid for it), and perhaps for similar reasons, I don’t think that matters to the production and sale of new ones. That article supports some of my claims about the glut of modern pianos and falls in price, and hence the claim that there may be unusually many pianos around now than in earlier centuries:
At least, if we’re comparing against the 1700s/1800s, since the article then goes on to give sales figures:
(Queen Victoria died in 1901, so if this golden age 1900-1930 also populated parlors, it would be more accurate to call it an ‘Edwardian parlor’.)
We got ~$75 for one we picked up out of somebody garbage in a garage sale, and given the high interest we had in it, probably could have gotten twice that. (Had an exchange student living with us who loved playing the piano, and when we saw it, we had to get it—it actually played pretty well, too, only three of the chords needed replacement. It was an experience loading that thing into a pickup truck without any equipment. Used a trash length of garden hose as rope and a -lot- of brute strength.)
I was basing my notion on having heard that a piano was a standard feature of a Victorian parlor. The original statement of the problem just specifies a piano, though I grant that the cartoon version requires a grand or baby grand. An upright piano just wouldn’t be as funny.
These days, there isn’t any musical instrument which is a standard feature in the same way. Instead, being able to play recorded music is the standard.
Thanks for the link about the lack of new musical instruments. I’ve been thinking for a while that stability of the classical orchestra meant there was something wrong, but it hadn’t occurred to me that we’ve got the same stability in pop music.
Sure, but think how small a fraction of the population that was. Most of Victorian England was, well, poor; coal miners or factory workers working 16 hour days, that sort of thing. Not wealthy bourgeoisie with parlors hosting the sort of high society ladies who were raised learning how to play piano, sketch, and faint in the arms of suitors.
Unless it’s set in a saloon! But given the low population density of the Old West, this is a relatively small error.
That article treats all forms of synthesis as one instrument. This is IMO not an accurate model. The explosion of electronic pop in the ’80s was because the technology was on the upward slope of the logistic curve, and new stuff was becoming available on a regular basis for artists to gleefully seize upon. But even now, there’s stuff you can do in 2013 that was largely out of reach, if not unknown, in 2000.
Have any handy examples? I find that a bit surprising (although it’s a dead cert that you know more about pop music than I do, so you’re probably right).
I’m talking mostly about new things you can do musically due to technology. The particular example I was thinking of was autotune, but that was actually invented in the late 1990s (whoops).
But digital signal processing in general has benefited hugely in Moore’s Law, and the ease afforded by being able to apply tens or hundreds of filters in real time. The phase change moment was when a musician could do this in faster than 1x time on a home PC. The past decade has been mostly on the top of the S-curve, though.
Nevertheless, treating all synthesis as one thing is simply an incorrect model.
Funny coincidence. About a week ago I was telling someone that people sometimes give autotune as an example of a qualitatively new musical/aural device, even though Godley & Creme basically did it 30+ years ago. (Which doesn’t contradict what you’re saying; just because it was possible to mimic autotune in 1979 doesn’t mean it was trivial, accessible, or doable in real time. Although autotune isn’t new, being able to autotune on an industrial scale presumably is, ’cause of Moore’s law.)
Granular synthesis is pretty fun.
Agreed, although I don’t know how impractical or unknown it was in 2000 — I remember playing with GranuLab on my home PC around 2001.
To 10m, surely?
The workplace fatalities really gone down recently, with all the safe jobs of sitting in front of the computer. You should look for workplace fatalities in construction, preferably historical (before safety guidelines). Accounting for that would raise the estimate.
A much bigger issue is that one has to actually stand under the piano as it is being lifted/lowered. The rate of such happening can be much (orders of magnitude) below that of fatal workplace accidents in general, and accounting for this would lower the estimate.
I don’t know where I would find them, and I’d guess that any reliable figures would be very recent: OSHA wasn’t even founded until the 1970s, by which point there’s already been huge shifts towards safer jobs.
That was the point of going for lifetime risks, to avoid having to directly estimate per-lifting fatality rates—I thought about it for a while, but I couldn’t see any remotely reasonable way to estimate how many pianos would fall and how often people would be near enough to be hit by it (which I could then estimate against number of pianos ever lifted to pull out a fatality rate, so instead I reversed the procedure and went with an overall fatality rate across all jobs).
You also need to account for the fact that some proportion of piano-hoister work-related fatalities will be to other factors like heatstroke or heart attack or wrapping the rope around their arm.
To a very good first approximation, the distribution of falling piano deaths is Poisson. So if the expected number of deaths is in the range [0.39, 39], then the probability that no one has died of a falling piano is in the range [1e-17, 0.677] which would lead us to believe that with a probability of at least 1⁄3 such a death has occurred. (If 3.9 were the true average, then there’s only a 2% chance of no such deaths.)
I disagree that the lower bound is 0; the right range is [-39,39]. Because after all, a falling piano can kill negative people: if a piano had fallen on Adolf Hitler in 1929, then it would have killed −5,999,999 people!
Sorry. The probability is in the range [1e-17, 1e17].
That is a large probability.
It’s for when you need to be a thousand million billion percent sure of something.
That approximation looks like this
It’ll overestimate by a lot if you do it over longer time periods. e.g. it overestimates this average by about 50% (your estimate actually gives 375, not 325), but if you went from 1m to 700m it would overestimate by a factor of about 3.
A pretty-easy way to estimate total population under exponential growth is just current population 1/e lifetime. From your numbers, the population multiplies by e^2.5 in 300 years, so 120 years to multiply by e. That’s two lifetimes, so the total number of lives is 700m2. For a smidgen more work you can get the “real” answer by doing 700m 2 − 50m 2.
Cecil Adams tackled this one. Although he could find no documented cases of people being killed by a falling piano (or a falling safe), he did find one case of a guy being killed by a RISING piano while having sex with his girlfriend on it. What would you have estimated for the probability of that?
From the webpage:
Reality really is stranger than fiction, is it.
You did much better in Example #2 than you thought; the conclusion should read
which looks like a Fermi victory (albeit an arithmetic fail).
Lol! Fixed.
There are 3141 counties in the US. This is easy to remember because it’s just the first four digits of pi (which you already have memorised, right?).
This reminds me of the surprisingly accurate approximation of pi x 10^7 seconds in a year.
This chart has been extremely helpful to me in school and is full of weird approximation like the two above.
Thanks for writing this! This is definitely an important skill and it doesn’t seem like there was such a post on LW already.
Some mild theoretical justification: one reason to expect this procedure to be reliable, especially if you break up an estimate into many pieces and multiply them, is that you expect the errors in your pieces to be more or less independent. That means they’ll often more or less cancel out once you multiply them (e.g. one piece might be 4 times too large but another might be 5 times too small). More precisely, you can compute the variance of the logarithm of the final estimate and, as the number of pieces gets large, it will shrink compared to the expected value of the logarithm (and even more precisely, you can use something like Hoeffding’s inequality).
Another mild justification is the notion of entangled truths. A lot of truths are entangled with the truth that there are about 300 million Americans and so on, so as long as you know a few relevant true facts about the world your estimates can’t be too far off (unless the model you put those facts into is bad).
If success of a fermi estimate is defined to be “within a factor of 10 of the correct answer”, then that’s a constant bound on the allowed error of the logarithm. No “compared to the expected value of the logarithm” involved. Besides, I wouldn’t expect the value of the logarithm to grow with number of pieces either: the log of an individual piece can be negative, and the true answer doesn’t get bigger just because you split the problem into more pieces.
So, assuming independent errors and using either Hoeffding’s inequality or the central limit theorem to estimate the error of the result, says that you’re better off using as few inputs as possible. The reason fermi estimates even involve more than 1 step, is that you can make the per-step error smaller by choosing pieces that you’re somewhat confident of.
Oops, you’re absolutely right. Thanks for the correction!
Tip: frame your estimates in terms of intervals with confidence levels, i.e. “90% probability that the answer is within and ”. Try to work out both a 90% and a 50% interval.
I’ve found interval estimates to be much more useful than point estimates, and they combine very well with Fermi techniques if you keep track of how much rounding you’ve introduced overall.
In addition, you can compute a Brier score when/if you find out the correct answer, which gives you a target for improvement.
Douglas W. Hubbard has a book titled How to Measure Anything where he states that half a day of exercising confidence interval calibration makes most people nearly perfectly calibrated. As you noted and as is said here, that method fits nicely with Fermi estimates.
This combination seems to have a great ratio between training time and usefulness.
I will note that I went through the mental exercise of cars in a much simpler (and I would say better) way: I took the number of cars in the US (300 million was my guess for this, which is actually fairly close to the actual figure of 254 million claimed by the same article that you referenced) and guessed about how long cars typically ended up lasting before they went away (my estimate range was 10-30 years on average). To have 300 million cars, that would suggest that we would have to purchase new cars at a sufficiently high rate to maintain that number of vehicles given that lifespan. So that gave me a range of 10-30 million cars purchased per year.
The number of 5 million cars per year absolutely floored me, because that actually would fail my sanity check—to get 300 million cars, that would mean that cars would have to last an average of 60 years before being replaced (and in actuality would indicate a replacement rate of 250M/5M = 50 years, ish).
The actual cause of this is that car sales have PLUMMETED in recent times. In 1990, the median age of a vehicle was 6.5 years; in 2007, it was 9.4 years, and in 2011, it was 10.8 years—meaning that in between 2007 and 2011, the median car had increased in age by 1.4 years in a mere 4 years.
I will note that this sort of calculation was taught to me all the way back in elementary school as a sort of “mathemagic”—using math to get good results with very little knowledge.
But it strikes me that you are perhaps trying too hard in some of your calculations. Oftentimes it pays to be lazy in such things, because you can easily overcompensate.
Would it bankrupt the global economy to orbit all the world’s Sikhs?
See also “Applying the Fermi Estimation Technique to Business Problems.”
http://t.www.na-businesspress.com/JABE/Jabe105/AndersonWeb.pdf I think this might be the updated link.
Write down your own Fermi estimation attempts here. One Fermi estimate per comment, please!
One famous Fermi estimate is the Drake equation.
A running list of my own: http://www.gwern.net/Notes#fermi-calculations (And there’s a number of them floating around predictionbook.com; Fermi-style loose reasoning is great for constraining predictions.)
Here’s one I did with Marcello awhile ago: about how many high schools are there in the US?
My attempt: there are 50 states. Each state has maybe 20 school districts. Each district has maybe 10 high schools. So 50 20 10 = 10,000 high schools.
Marcello’s attempt (IIRC): there are 300 million Americans. Of these, maybe 50 million are in high school. There are maybe 1,000 students in a high school. So 50,000,000 / 1,000 = 50,000 high schools.
Actual answer:
...
...
...
Numbers vary, I think depending on what is being counted as a high school, but it looks like the actual number is between 18,000 and 24,000. As it turns out, the first approach underestimated the total number of school districts in the US (it’s more like 14,000) but overestimated the number of high schools per district. The second approach overestimated the number of high school students (it’s more like 14 million) but also overestimated the average number of students per high school. And the geometric mean of the two approaches is 22,000, which is quite close!
I tried the second approach with better success: it helps to break up the “how many Americans are in high school” calculation. If the average American lives for 80 years, and goes to high school for 4, then 1⁄20 of all Americans are in high school, which is 15 million.
...you guessed 1 out of 6 Americans is in highschool?
With an average lifespan of 70+ years and a highschool duration of 3 years (edit: oh, it’s 4 years in the US?), shouldn’t it be somewhere between 1 in 20 and 1 in 25?
This conversation happened something like a month ago, and it was Marcello using this approach, not me, so my memory of what Marcello did is fuzzy, but IIRC he used a big number.
The distribution of population shouldn’t be exactly uniform with respect to age, although it’s probably more uniform now than it used to be.
Just tried one today: how safe are planes?
Last time I was at an airport, the screen had five flights, three-hour period. It was peak time, so multiplied only by fifteen, so 25 flights from Chennai airport per day.
~200 countries in the world, so guessed 500 adjusted airports (effective no. of airports of size of Chennai airport), giving 12500 flights a day and 3*10^6 flights a year.
One crash a year from my news memories, gives possibility of plane crash as 1⁄310^-6 ~ 310^-7.
Probability of dying in a plane crash is 3*10^-7 (source). At hundred dead passengers a flight, fatal crashes are ~ 10^-5. Off by two orders of magnitude.
If there are 310^6 flights in a year, and one randomly selected plane crashes per year on average, with all aboard being killed, then the chances of dying in an airplane crash are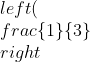
Yes, there’s a hundred dead passengers on the flight that went down, but there’s also a hundred living passengers on every flight that didn’t go down. The hundreds cancel out.
Wow, that was stupid of me. Of course they do! And thanks.
Anna Salamon’s Singularity Summit talk from a few years ago explains one Fermi estimate regarding the value of gathering more information about AI impacts: How Much it Matters to Know What Matters: A Back of the Envelope Calculation.
How old is the SECOND oldest person in the world compared to the oldest? Same for the united states?
I bogged down long before I got the answer. Below is the gibberish I generated towards bogging down.
So OK, I don’t even know offhand how old is the oldest, but I would bet it is in the 114 years old (yo) to 120 yo range.
Then figure in some hand-wavey way that people die at ages normally distributed with a mean of 75 yo. We can estimate how many sigma (standard deviations) away from that is the oldest person.
Figure there are 6 billion people now, but I know this number has grown a lot in my lifetime, it was less than 4 billion when I was born 55.95 years ago. So say the 75 yo’s come from a population consistent with 3 billion people. 1⁄2 die younger than 75, 1⁄2 die older, so the oldest person in the world is 1 in 1.5 billion on the distribution.
OK what do I know about normal distributions? Normal distribution goes as exp ( -((mean-x)/(2sigma))^2 ). So at what x is exp( -(x/2sigma)^2 ) = 1e-9? (x / 2sigma) ^ 2 = -ln ( 1e-9). How to estimate natural log of a billionth? e = 2.7 is close enough for government work to the sqrt(10). So ln(z) = 2log_10(z). Then -ln(1e-9) = −2log_10(1e-9) = 29 = 18. So (x/2sigma)^2 = 18, sqrt(18) = 4 so
So I got 1 in a billion is 4 sigma. I didn’t trust that so I looked that up, Maybe I should have trusted it, in fact 1 in a billion is (slightly more than ) 6 sigma.
mean of 75 yo, x=115 yo, x-mean = 40 years. 6 sigma is 40 years. 1 sigma=6 years.
So do I have ANYTHING yet? I am looking for dx where exp(-((x+dx)/(2sigma))^2) - exp( -(x/2sigma)^2)
So, this isn’t quite appropriate for Fermi calculations, because the math involved is a bit intense to do in your head. But here’s how you’d actually do it:
Age-related mortality follows a Gompertz curve, which has much, much shorter tails than a normal distribution.
I’d start with order statistics. If you have a population of 5 billion people, then the expected percentile of the top person is 1-(1/10e9), and the expected percentile of the second best person is 1-(3/10e9). (Why is it a 3, instead of a 2? Because each of these expectations is in the middle of a range that’s 1/5e9, or 2/10e9, wide.)
So, the expected age* of death for the oldest person is 114.46, using the numbers from that post (and committing the sin of reporting several more significant figures), and the expected age of death for the second oldest person is 113.97. That suggests a gap of about six months between the oldest and second oldest.
* I should be clear that this is the age corresponding to the expected percentile, not the expected age, which is a more involved calculation. They should be pretty close, especially given our huge population size.
But terminal age and current age are different- it could actually be that the person with the higher terminal age is currently younger! So we would need to look at permutations and a bunch of other stuff. Let’s ignore this and assume they’ll die on the same day.
So what does it look like in reality?
The longest lived well-recorded human was 122, but note that she died less than 20 years ago. The total population whose births were well-recorded is significantly smaller than the current population, and the numbers are even more pessimistic than the 3 billion figure you get at; instead of looking at people alive in the 1870s, we need to look at the number born in the 1870s. Our model estimates she’s a 1 in 2*10^22 occurrence, which suggests our model isn’t tuned correctly. (If we replace the 10 with a 10.84, a relatively small change, her age is now the expectation for the oldest terminal age in 5 billion- but, again, she’s not out of a sample of 5 billion.)
The real gaps are here; about a year, another year, then months. (A decrease in gap size is to be expected, but it’s clear that our model is a bit off, which isn’t surprising, given that all of the coefficients were reported at 1 significant figure.)
Upvoted (among other things) for a way of determining the distribution of order statistics from an arbitrary distribution knowing those of a uniform distribution which sounds obvious in retrospect but to be honest I would never have come up with on my own.
Assuming dx << x, this is approximated by a differential, (-xdx/sigma^2) * exp( -(x/2sigma)^2, or the relative drop of dx/sigma^2. You want it to be 1⁄2 (lost one person out of two), your x = 4 sigma, so dx=1/8 sigma, which is under a year. Of course, it’s rather optimistic to apply the normal distribution to this problem, to begin with.
I estimated how much the population of Helsinki (capital of Finland) grew in 2012. I knew from the news that the growth rate is considered to be steep.
I knew there are currently about 500 000 habitants in Helsinki. I set the upper bound to 3 % growth rate or 15 000 residents for now. With that rate the city would grow twentyfold in 100 years which is too much. But the rate might be steeper now. For lower bound i chose 1000 new residents. I felt that anything less couldnt really produce any news. AGM is 3750.
My second method was to go through the number of new apartments. Here I just checked that in recent years about 3000 apartments have been built yearly. Guessing that the household size could be 2 persons I got 6000 new residents.
It turned out that the population grew by 8300 residents which is highest in 17 years. Otherwise it has recently been around 6000. So both methods worked well. Both have the benefit that one doesnt need to care whether the growth comes from births/deaths or people flow. They also didn’t require considering how many people move out and how many come in.
Obviously i was much more confident on the second method. Which makes me think that applying confidence intervals to fermi estimates would be useful.
For the “Only Shallow” one, I couldn’t think of a good way to break it down, and so began by approximating the total number of listens at 2 million. My final estimate was off by a factor of one.
Matt Mahoney’s estimate of the cost of AI is a sort-of Fermi estimate.
Out of the price of a new car, how much goes to buying raw materials? How much to capital owners? How much to labor?
How many Wall-Marts in the USA.
That sounds like the kind of thing you could just Google.
But I’ll bite. Wal-Marts have the advantage of being pretty evenly distributed geographically; there’s rarely more than one within easy driving distance. I recall there being about 15,000 towns in the US, but they aren’t uniformly distributed; they tend to cluster, and even among those that aren’t clustered a good number are going to be too small to support a Wal-Mart. So let’s assume there’s one Wal-Mart per five towns on average, taking into account clustering effects and towns too small or isolated to support one. That gives us a figure of 3,000 Wal-Marts.
When I Google it, that turns out to be irel pybfr gb gur ahzore bs Jny-Zneg Fhcrepragref, gur ynetr syntfuvc fgberf gung gur cuenfr “Jny-Zneg” oevatf gb zvaq. Ubjrire, Jny-Zneg nyfb bcrengrf n fznyyre ahzore bs “qvfpbhag fgber”, “arvtuobeubbq znexrg”, naq “rkcerff” ybpngvbaf gung funer gur fnzr oenaqvat. Vs jr vapyhqr “qvfpbhag” naq “arvtuobeubbq” ybpngvbaf, gur gbgny vf nobhg guerr gubhfnaq rvtug uhaqerq. V pna’g svaq gur ahzore bs “rkcerff” fgberf, ohg gur sbezng jnf perngrq va 2011 fb gurer cebonoyl nera’g gbb znal.
Different method. Assume all 300 million us citizens are served by a Wal Mart. Any population that doesn’t live near a Wal-Mart has to be small enough to ignore. Each Wal-mart probably has between 10,000 and 1 million potential customers. Both fringes seem unlikely, so we can be within a factor of 10 by guessing 100000 people per Wal-Mart. This also leads to 3000 Wal-Marts in the US.
I’m not sure about this claim about day-to-day life. Maybe there are some lines of work where this skill could be useful, but in general it’s quite rare in day-to-day life where you have to come up with quick estimates on the spot to make a sound descision. Many things can be looked up on the internet for a rather marginal time-cost nowadays. Often enough probably even less time, than it would actually take someone to calculate the guesstimate.
If a descision or statistic is important you, should take the time to actually just look it up, or if the information you are trying to guess is impossible to find online, you can at least look up some statistics that you can and should use to make your guess better. As you read above, just getting one estimate in a long line of reasoning wrong (especially where big numbers are concerned) can throw off your guess by a factor of 100 or 1000 and make it useless or even harmful.
If your guess is important to an argument you’re constructing on-the-fly, I think you could also take the time to just look it up. (If it’s not an interview or some conversation which dictates, that using a smartphone would be unacceptable).
And if a descision or argument is not important enough to invest some time in a quick online search, then why bother in the first place? Sure, it’s a cool skill to show off and it requires some rationality, but that doesn’t mean it’s truly useful. On the other hand maybe I’m just particularly unimaginative today and can’t think of ways, how Fermi estimates could possibly improve my day-to-day life by a margin that would warrant the effort to get better at it.
The guys at last.fm are usually very willing to help out with interesting research (or at least were when I worked there a couple of years ago), so if you particularly care about that information it’s worth trying to contact them.
http://www.fermiquestions.com/ link doesn’t work anymore. It is also not on wayback machine. :(
You can try estimating, or keep listing the reasons why it’s hard.
One of my favorite numbers to remember to aid in estimations is this: 1 year = pi * 10^7 seconds. Its really pretty accurate.
Of course for Fermi estimation just remember 1 Gs (gigasecond) = 30 years.
10^7.5 is even more accurate.
I spend probably a pretty unusual amount of time estimating things for fun, and have come to use more or less this exact process on my own over time from doing it.
One thing I’ve observed, but haven’t truly tested, is my geometric means seem to be much more effective when I’m willing to put a more tight guess on them. I started off bounding them with what I thought the answer conceivably could be, which seemed objective and often felt easier to estimate. The problem was that often either the lower or upper bound was too arbitrary relative to it’s weight on my final estimate. Say, average times an average 15 year old sends an mms photo in a week. My upper bound may be 100ish but my lower bound could be 2 almost as easily as it could be 5 which ranges my final estimate quite a bit, between 14 and 22.
To help remember this post and it’s methods I broke it down into song lyrics and used Udio to make the song.
Check out https://www.fermiproblems.in/ for a great collection of guesstimates / fermiproblems
I just wanted to say, after reading the Fermi estimate of cars in the US, I literally clapped—out loud. Well done. And I highly appreciate the honest poor first attempt—so that I don’t feel like such an idiot next time I completely fail.
Potentially useful: http://instacalc.com/
I’m happy to see that the Greatest Band of All Time is the only rock band I can recall ever mentioned in a top-level LessWrong post. I thought rationalists just sort of listened only to Great Works like Bach or Mozart, but I guess I was wrong. Clearly lukeprog used his skills as a rationalist to rationally deduce the band with the greatest talent, creativity, and artistic impact of the last thirty years and then decided to put a reference to them in this post :)
If you check out Media posts, you’ll see that LWers like a range of music. It wouldn’t surprise me too much if they tend to like contemporary classical better than classical classical.
I like a specific subset of classical classical, but I suspect not at all typical.
Why?
Because of the images of different musical genres in our culture. There is an association of classical music and being academic or upper class. In popular media, liking classical music is a cheap signal for these character types. This naturally triggers confirmation biases, as we view the rationalist listening to Bach as typical, and the rationalist listening to The Rolling Stones as atypical. People also use musical preference to signal what type of person they are. If someone wants to be seen as a rationalist, they often mention their love of Bach and don’t mention genres with a different image, except to disparage them.
I think you’re conflating “rationalist” and “intellectual.” I agree that there is a stereotype that intellectuals only listen to Great Works like Bach or Mozart, but I’m curious where the OP picked up that this stereotype also ought to apply to LW-style rationalists. I mean, Eliezer takes pains in the Sequences to make anime references specifically to avoid this kind of thing.
Well, he also likes tends to like anime, and anime has a tendency to deal with some future-ish issues.
From On Things That Are Awesome:
I’m just pointing out the way such a bias comes into being. I know I don’t listen to classical, and although I’d expect a slightly higher proportion here than in the general population, I wouldn’t guess it wold be a majority or significant plurality.
If I had to guess, I’d guess on varied musical tastes, probably trending towards more niche genres than broad spectrum pop than the general population.
Well, Eliezer mentions Bach a bunch in the sequences as an example of a great work of art. I used stereotypes to extrapolate. :p
(the statement was tongue-in-cheek, if that didn’t come across. I am genuinely a little surprised to see MBV mentioned here though.)
I recently ran across an article describing how to find a rough estimate of the standard deviation of a population, given a number of samples, which seems that it would be suitable for Fermi estimates of probability distributions.
First of all, you need a large enough population that the central limit theorem applies, and the distribution can therefore be assumed to be normal. In a normal distribution, 99.73% of the samples will be within three standard deviations of the mean (either above or below; a total range of six standard deviations). Therefore, one can roughly estimate the standard deviation by taking the largest value, subtracting the smallest value, and dividing the result by 6.
Source
This is useful, because in a normal distribution, around 7 in 10 of the samples will be within one standard deviation of the mean, and around 19 in every 20 will be within two standard deviations of the mean.
If you want a range containing 70% of the samples, why wouldn’t you just take the range between the 15th and 85th percentile values?
That would also work, and probably be more accurate, but I suspect that it would take longer to find the 15th and 85th percentile values than it would to find the ends of the range.
How long can the International Space Station stay up without a boost? I can think of a couple of ways to estimate that.
Out of the price of a new car, how much goes to buying raw materials? How much to capital owners? How much to labor?
I recommend trying to take the harmonic mean of a physical and an economic estimate when appropriate.
I recommend doing everything when appropriate.
Is there a particular reason why the harmonic mean would be a particularly suitable tool for combining physical and economic estimates? I’ve spent only a few seconds trying to think of one, failed, and had trouble motivating myself to look harder because on the face of it it seems like for most problems for which you might want to do this you’re about equally likely to be finding any given quantity as its reciprocal, which suggests that a general preference for the harmonic mean is unlikely to be a good strategy—what am I missing?
Can I have a representative example of a problem where this is appropriate?
So, what you’re saying is that the larger number is less likely to be accurate the further it is from the smaller number? Why is that?