What’s going on? LLMs and IS-A sentences
This is a cross-post from New Savanna.
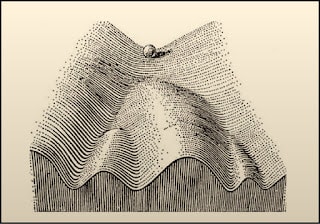
For the moment I have decided that Waddington’s classic diagram of the epigenetic landscape is a useful way of thinking about when happens when an LLM responds to a prompt. Here’s the diagram:
The language model corresponds to the landscape. The prompt serves to position that ball at a certain place in the landscape – perhaps we can think of that ball as the prompt. The ball then rolls down the valley, going left and right as appropriate. It never reverses direction and goes up the hill. That path, or trajectory if you will, is the LLM’s response to the prompt.
Moreover, I have decided to think of the generation of each word (yes, I know, technically it spits out tokens, not words) as a single primitive operation. That is to say, it has no internal logical structure, no ANDs or ORs. It’s simply one (gigantic) calculation over roughly 175 billion values (in the case of ChatGPT). The generation of each word presents the system with a choice among alternatives, but that’s the only kind of choice involved in calculating the response to a prompt – though for qualification and elaboration, see ChatGPT tells stories, and a note about reverse engineering: A Working Paper, Version 3, pp. 3-6.
That brings me to something I’ve been puzzled about for years. We find it natural to say things like, Garfield is a cat. Now, express the same thought, but reverse the order of cat and Garfield in your sentence. It’s difficult to do. Oh, you can do it, but the resulting sentence is awkward and unnatural, something like, Cats are the kind of thing of which Garfield is a particular instance. No one would ever speak like that, nor write it either.
What’s the source of that asymmetry? As far as I can tell, we don’t know, but I take it as a clue about the mechanisms of language. The purpose of this note is to suggest that my crude model of LLM calculation would provide an answer: The linguistic landscape is structured so that the ball easily rolls from Garfield to cat, or cat to mammal, Snoopy to beagle, Tesla to EV, C. elegans to worm, etc. One might, of course, as why the landscape is arranged in that way, but that’s a different question, no?
Here’s some notes I made about IS-A sentences.
Notes on IS-A Sentences
Somewhere in his Problems in General Linguistics, my copy of which is, alas, in storage, Emile Benveniste has a chapter, “The Nominal Sentence,” on sentences hanging on the auxiliary “to be.” As Benveniste was a linguist of the Old School, when being a linguistic meant familiarity with many languages, including—and this is important for this particular topic—classical Greek, it had examples from many languages, making it tough sledding for a monoglot like me.
While the content of this post certainly arises out of my thinking about that chapter, in the absence of actually having the text in front of me, I hesitate to assert a stronger relationship than that. I note only that, for Benveniste, the auxiliary “to be” was fraught with metaphysical significance. For the concept of being derives from “to be.” Where would philosophy be without Being? Thus, when Benveniste pondered such sentences, he wasn’t merely commenting on language. He was doing philosophy, or, if not quite that, camping out on philosophy’s door step.
I’m interested in such sentences because I believe they are a DEEP CLUE about how the mind works. I just don’t know what to make of the clue.
So, I’m interested in word order in assertions such as the following:
(1) Fido is a beagle.
(2) Beagles are dogs.
(3) Dogs are beasts.
They all move from an element in a class (whether an individual, Fido, or another class, beagles) to a class containing it. None of them move in the opposite direction. Consider what happens when you try to go the opposite way. In the following sentence the class is mentioned first, then the subclass:
(4) Beagle is the kind of animal of which Fido is an instance.
In particular, note that (4) has a metalingual character that (1) does not. That is, (4) explicitly asserts that we are dealing with classification. One can do that metalingual job in various ways, but, as far as I can tell, one can’t avoid it. That is, one cannot construct a proper English sentence relating a genus and species in which the genus is mentioned first, one can’t do that without ‘looping through’ some kind of metalingual construction on the way from genus to species.
Why?
What does this assymetry tell us about the underlying mechanisms? Why don’t have sentences such as:
(5) Beagle za di Fido.
In this case “za di” is the inverse of “is a”. English has no such sentences & no such inverse.
So, how widespread is this asymmetry and is there any explanation of this directionality?
I sent a query on that matter to a listserve, I forget which one, and got two replies that add some complexity to the matter. Rich Rhodes, Linguistics at UCal Berkeley, tells me that in Ojibwe the word order is reversed, the class comes before the individual, but the asymmetry remains. He then comments, which he qualifies as a quick guess:
My guess is that there is no compelling discourse function (like information flow) which makes it desirable to invert classificational equatives. Hence we only get the “unmarked” order. Subject-predicate in theme-rheme languages (like English) and predicate-subject in rheme-theme languages (like Ojibwe).
So, what’s the nature of the mechanism that determines the “unmarked” order? That’s what I want to know.
Lee Pearcy, Episcopal Academy in Merion, Pa. offered these examples:
(6) The beagle is Fido.
(7) The dogs are beagles.
(8) The beasts are dogs.
As stand-alone sentences, they seem a bit awkward to me. But they fare better as answers to questions, e.g.:
What’s that dog?
Which dog? The beagle is Fido and the terrier is Max.
What’re those animals?
The dogs are beagles, the cats are Persians.
In those contexts, the matter of class or classification is raised by the question, thus making it present in the discourse and so available as a point of attachment in the answer.
Further clues, anyone?
Do I believe this?
I don’t believe it, or disbelieve it. It’s a working hypothesis. One I think is worth investigating. It places relatively simple and severe constraints on our conception of what LLMs are doing. That, it seems to me, is a good thing. Should it turn out that those constraints are valid, well then, we’ve learned something, no? If they’re not valid, we’ve also learned something.
More later.
Contains/element-of are the complementary formal verbs from set theory, but I’ve definitely seen Contains/is-a used as equivalent in practice (cats contains Garfield because Garfield is a cat).
Similarly in programming “cat is Garfield’s type” makes sense although it’s verbose, or “cat is implemented by Garfield” for the traits folks which is far more natural.
So where linguistically necessary humans have had no trouble complementing is-a in natural language. I think it’s a matter of where emphasis is desired; usually the subject (Garfield) is where the emphasis is, and usually the element is the subject instead of the class. Formally we often want the class/set/type to be the subject since it’s the thing we are emphasizing.
Umm, I think you’re putting too much weight on idiomatic shorthand that’s evolved for communicating some common things very easily, and less-common ideas less easily. “Garfield is a cat” is a very reasonable and common thing to try to communicate—a specific not-well-known thing (garfield) being described in terms of a nearly-universal knowledge (“cat”). The reverse might be “Cats are things like Garfield”, which is a bit odd because the necessity of communicating it is a bit odd.
It tends to track specific to general, not because they’re specific or general concepts, but because specifics more commonly need to be described than generalities.
I don’t think there’s anything particularly idiomatic about “is a,” but that’s a side issue. What’s at issue are the underlying linguistic mechanisms. How do they work? Sure, some communicative tasks may be more common than others, and that is something to take into account. Linguistic mechanisms that are used frequently tend to be more compact than those used less frequently, for obvious reasons. Regardless of frequency, how do they work?
Interesting post. Two comments:
Which seems natural enough to me, though I don’t disagree that what you point out is interesting. I was recently reading parts of Analytical Archaeology, David Clark (1978) where he goes into some detail about the difference between artifacts and artifact-types. Seems like you are getting at statements like
Where the is-a maps from an artifact to its type. It would make intuitive sense to me that languages would have a preferred orientation w.r.t such a mapping—this is the core of abstraction, which is at the core of language.
So it seems like in English we prefer to further up the stack of abstractions when using is-a, thus:
etc., and if you wanted to go down the stack you have to say eg:
So is-a is just a way of moving up the ladder of abstractions? (<- movements up the ladder of abstractions such as this sentence here)
Two comments:
1) One could say something like, “Beagles, such as Fido, are known to...” There your four-word phrase is part of a larger construction and is subject to the rules and constraints involved in such a construction.
2) You’re correct about “is-a”. Back in the days of symbolic AI, “ISA” was often used as an arc label in semantic network constructions. “Dog,” “pony,” and “cat,” would be linked to, say, “beast” by the ISA arc, “beast,” “fish,” and “insect” would be lined to “plant” by the ISA arc, etc. So, you’re right, it’s a device for moving up and down paradigmatic trees, as linguists would call them. Such trees are ubiquitous.
That’s why that particular construction interests me. And the fact the movement along ISA chains is syntactically easy going in one direction, but not the other direction (though there are ways of doing it and contexts in which it is natural), is therefore interesting as well. Given that we are, after all, talking about computation, the way you have to move around some conceptual structure in the course of computing over/with it, that tells us something about how the mechanism works.
“(I saw) a dog, specifically, a beagle,”
or if you’re willing to sound a little old fashioned and long-winded:
“(I saw) a dog, or, more specifically, a beagle, or yet more specifically, Fido.”
So the construction exits and isn’t quite as contrived as your version. But I agree, it doesn’t exactly roll off the tongue. And it only works as a noun clause, rather than an entire sentence.
And asserting that you saw something is different from asserting what something is. You can do the latter without ever having seen that something yourself, but you know about it because you read it in a book or someone told you about. So it’s not semantically equivalent. As you say, it works only as a clause, not as a free-standing sentence.
Hi, friends,
in my opinion, this asymmetry can be explained if we consider natural language as a tool for modeling the internal space of knowledge in which the individual’s consciousness operates, while knowledge is a tool for modeling what the individual considers the surrounding reality. If we talk about knowledge as the structure of concepts, then this structure is usually presented in the form of a hierarchy, so moving down from the general to the specific is natural and less energy/information intensive.
But what if knowledge has a fractal structure?… What do you think of that?
But in assertions such as “beagles are dogs” and “eagles are birds” etc. we’re moving UP from specific to general, not down.
Surely, sorry, I’ve meant that moving from specific to general, which is corresponds to moving from state, characterized by less entropy to state, with higher entropy.
Another fairly natural phrasing for putting the category before the instance would be to say that “this cat is Garfield”
Or slightly less naturally, “cats include Garfield”. Which doesn’t work wonderfully well for that example but does see use in other cases like “my hobbies include...”
I don’t think “hobbies” is the same kind of thing. One of the ideas that comes along with the idea of paradigmatic structure is that of inheritance, which you may know from object-oriented programming languages. So, “animal” has certain characteristics that are true for all animals. “Beast” inherits those characteristics plus those that are characteristic of beasts, but not birds or fish or insects. Likewise, “insect” inherits the general characteristics of animals, plus those true of insects, but not of beats, fish, and birds, and so on. Similarly, “cattle” inherits from “beast,” “robin” from “bird,” and so on. I don’t think “hobby” works like that. A wide variety of activities can serve as hobbies, but not necessarily so. Making ceramic pots is a hobby for one person, but an occupation for another. Card tricks are work activities for a magician, but a hobby for someone else. And so on.
It’s been noted that there’s a general tendency in many languages to put presuppositions early in sentences. I can’t say I’ve read or thought much about why, but at the very least this seems to follow the likely temporal order of how the assertion was formed, e.g. I can’t make any assertion about Garfield if I don’t first assume he exists.
In, “Garfield is a cat,” we are implicitly assuming that there exists some individual Garfield. In the answer to the question of the cat’s identity, we would say, “The cat is Garfield,” because our answer is contingent on the fact that there is some cat that is being referenced. By, contrast, “Garfield is the cat,” as a response sounds much less natural.
One other way of putting the reverse order, though it sounds a bit stilted in English: “beagles have Fido”. I don’t think it’s used commonly at all but it came to mind as a form in the reverse order without looping.
Sure, we can do all sort of things with language if we put our minds to it. That’s not the point. What’s important is how do people actually use language. In the corpus of texts used to train, say, GPT-4, how many times is the phrase “beagles have Fido” likely to have occurred?