Decision theory: Why we need to reduce “could”, “would”, “should”
(This is the second post in a planned sequence.)
Let’s say you’re building an artificial intelligence named Bob. You’d like Bob to sally forth and win many utilons on your behalf. How should you build him? More specifically, should you build Bob to have a world-model in which there are many different actions he “could” take, each of which “would” give him particular expected results? (Note that e.g. evolution, rivers, and thermostats do not have explicit “could”/“would”/“should” models in this sense—and while evolution, rivers, and thermostats are all varying degrees of stupid, they all still accomplish specific sorts of world-changes. One might imagine more powerful agents that also simply take useful actions, without claimed “could”s and “woulds”.)
My aim in this post is simply to draw attention to “could”, “would”, and “should”, as concepts folk intuition fails to understand, but that seem nevertheless to do something important for real-world agents. If we want to build Bob, we may well need to figure out what the concepts “could” and “would” can do for him.*
Introducing Could/Would/Should agents:
Let a Could/Would/Should Algorithm, or CSA for short, be any algorithm that chooses its actions by considering a list of alternatives, estimating the payoff it “would” get “if” it took each given action, and choosing the action from which it expects highest payoff.
That is: let us say that to specify a CSA, we need to specify:
A list of alternatives a_1, a_2, …, a_n that are primitively labeled as actions it “could” take;
For each alternative a_1 through a_n, an expected payoff U(a_i) that is labeled as what “would” happen if the CSA takes that alternative.
To be a CSA, the algorithm must then search through the payoffs for each action, and must then trigger the agent to actually take the action a_i for which its labeled U(a_i) is maximal.
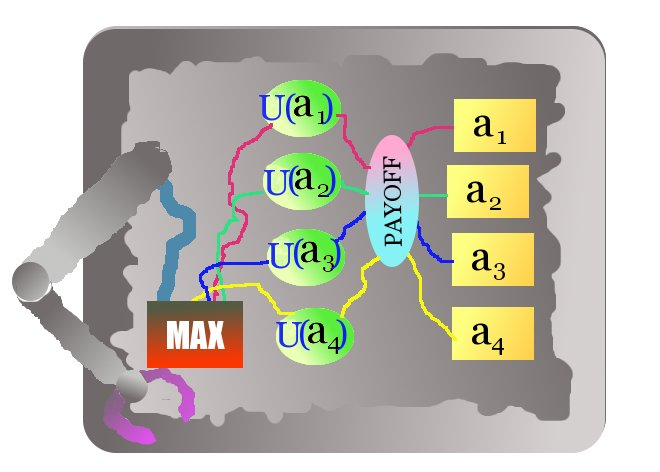
Note that we can, by this definition of “CSA”, create a CSA around any made-up list of “alternative actions” and of corresponding “expected payoffs”.
The puzzle is that CSAs are common enough to suggest that they’re useful—but it isn’t clear why CSAs are useful, or quite what kinds of CSAs are what kind of useful. To spell out the puzzle:
Puzzle piece 1: CSAs are common. Humans, some (though far from all) other animals, and many human-created decision-making programs (game-playing programs, scheduling software, etc.), have CSA-like structure. That is, we consider “alternatives” and act out the alternative from which we “expect” the highest payoff (at least to a first approximation). The ubiquity of approximate CSAs suggests that CSAs are in some sense useful.
Puzzle piece 2: The naïve realist model of CSAs’ nature and usefulness doesn’t work as an explanation.
That is: many people find CSAs’ usefulness unsurprising, because they imagine a Physically Irreducible Choice Point, where an agent faces Real Options; by thinking hard, and choosing the Option that looks best, naïve realists figure that you can get the best-looking option (instead of one of those other options, that you Really Could have gotten).
But CSAs, like other agents, are deterministic physical systems. Each CSA executes a single sequence of physical movements, some of which we consider “examining alternatives”, and some of which we consider “taking an action”. It isn’t clear why or in what sense such systems do better than deterministic systems built in some other way.
Puzzle piece 3: Real CSAs are presumably not built from arbitrarily labeled “coulds” and “woulds”—presumably, the “woulds” that humans and others use, when considering e.g. which chess move to make, have useful properties. But it isn’t clear what those properties are, or how to build an algorithm to compute “woulds” with the desired properties.
Puzzle piece 4: On their face, all calculations of counterfactual payoffs (“woulds”) involve asking questions about impossible worlds. It is not clear how to interpret such questions.
Determinism notwithstanding, it is tempting to interpret CSAs’ “woulds”—our U(a_i)s above—as calculating what “really would” happen, if they “were” somehow able to take each given action.
But if agent X will (deterministically) choose action a_1, then when he asks what would happen “if” he takes alternative action a _2, he’s asking what would happen if something impossible happens.
If X is to calculate the payoff “if he takes action a_2” as part of a causal world-model, he’ll need to choose some particular meaning of “if he takes action a_2” – some meaning that allows him to combine a model of himself taking action a_2 with the rest of his current picture of the world, without allowing predictions like “if I take action a_2, then the laws of physics will have been broken”.
We are left with several questions:
Just what are humans, and other common CSAs, calculating when we imagine what “would” happen “if” we took actions we won’t take?
In what sense, and in what environments, are such “would” calculations useful? Or, if “would” calculations are not useful in any reasonable sense, how did CSAs come to be so common?
Is there more than one natural way to calculate these counterfactual “would”s? If so, what are the alternatives, and which alternative works best?
*A draft-reader suggested to me that this question is poorly motivated: what other kinds of agents could there be, besides “could”/“would”/“should” agents? Also, how could modeling the world in terms of “could” and “would” not be useful to the agent?
My impression is that there is a sort of gap in philosophical wariness here that is a bit difficult to bridge, but that one must bridge if one is to think well about AI design. I’ll try an analogy. In my experience, beginning math students simply expect their nice-sounding procedures to work. For example, they expect to be able to add fractions straight across. When you tell them they can’t, they demand to know why they can’t, as though most nice-sounding theorems are true, and if you want to claim that one isn’t, the burden of proof is on you. It is only after students gain considerable mathematical sophistication (or experience getting burned by expectations that don’t pan out) that they place the burden of proofs on the theorems, assume theorems false or un-usable until proven true, and try to actively construct and prove their mathematical worlds.
Reaching toward AI theory is similar. If you don’t understand how to reduce a concept—how to build circuits that compute that concept, and what exact positive results will follow from that concept and will be absent in agents which don’t implement it—you need to keep analyzing. You need to be suspicious of anything you can’t derive for yourself, from scratch. Otherwise, even if there is something of the sort that is useful in the specific context of your head (e.g., some sort of “could”s and “would”s that do you good), your attempt to re-create something similar-looking in an AI may well lose the usefulness. You get cargo cult could/woulds.
+ Thanks to Z M Davis for the above gorgeous diagram.
- Original Research on Less Wrong by (29 Oct 2012 22:50 UTC; 49 points)
- Decision theory: Why Pearl helps reduce “could” and “would”, but still leaves us with at least three alternatives by (6 Sep 2009 6:10 UTC; 48 points)
- Solutions to Political Problems As Counterfactuals by (25 Sep 2009 17:21 UTC; 46 points)
- Decision theory: An outline of some upcoming posts by (25 Aug 2009 7:34 UTC; 31 points)
- Overcoming Clinginess in Impact Measures by (30 Jun 2018 22:51 UTC; 30 points)
- The Prediction Problem: A Variant on Newcomb’s by (4 Jul 2018 7:40 UTC; 25 points)
- MWI, weird quantum experiments and future-directed continuity of conscious experience by (18 Sep 2009 16:45 UTC; 6 points)
- Initial Thoughts on Dissolving “Couldness” by (22 Sep 2022 21:23 UTC; 6 points)
- Towards a New Decision Theory for Parallel Agents by (7 Aug 2011 23:39 UTC; 4 points)
- 's comment on Reference Post: Formal vs. Effective Pre-Commitment by (28 Aug 2018 0:26 UTC; 2 points)
- 's comment on Towards a New Decision Theory for Parallel Agents by (9 Aug 2011 21:25 UTC; 1 point)
Calculating what would happen if an agent took some action is not counter-factual from the POV of the agent. The agent doesn’t know what action it is going to take. If it did, it would just take the action—not spend time calculating the consequences of its various possible actions.
To be exact, the agent must not know “which action maximizes utility” not “which action it will do”. If it does whichever action it knows it’ll do, it can have Lob-type short circuits where you say “I know you’ll shoot yourself” and it says “OK thanks!” and shoots itself.
http://lesswrong.com/lw/t8/you_provably_cant_trust_yourself/
Here, let me go back in time and become timtyler and retroactively write the following instead, thereby averting this whole discussion:
Um, what?!?
Agents can and do decide to shoot themselves—and then go ahead and do it.
They don’t necessarily believe what other people tell them, though. Whether they do that depends—in part—on how suggestible and gullible they are.
I think Eliezer_Yudkowsky’s point was that people don’t necessarily shoot themselves merely because they considered it, and it is this kind of absurdity that is allowed whenever the agent only checks for whether it’s correctly predicted itself. (I may have gotten the exact phrasing on the last part wrong.)
Of course people don’t necessarily shoot themselves merely because they consider doing so. I don’t see what that has to do with the issue, though. I expect some kind of misunderstanding has arisen somewhere.
What it has to do with the issue is: the procedure Eliezer_Yudkowsky was criticizing would permit self-justifying actions such as shooting yourself because you consider it, which was why he pointed out the correct constraint an agent should follow.
Er, no it wouldn’t.
What I said was that if agents already knew what they were going to do, they would get on and do it—rather than doing more calculations about the issue.
That simply doesn’t imply they will commit suicide if someone tells them they will do that—because they don’t have to believe what people tell them.
I think people here are using a very weak definition of “know”. If I know that I will X, then I will X. If it later turns out that I didn’t X, then I did not actually know that I will X. That I will X is logically implied by anyone knowing that I will X.
I’m not sure how anyone could achieve actual knowledge of one’s future actions, but I agree that there’s little reason to deliberate over them if one does.
Often you know what your actions are going to be a split-second before you take them. After you have decided what to do but before the motor signals go out. That’s the type of advance-knowledge I was considering.
The information isn’t certain—but then NO information is certain.
Maybe.
it doesn’t imply that agent’s will kill themselves when you tell them they were going to, it implies that they can if you telling them is last scrap of bayesian evidence necessary to move the agent to act in that way. EY’s point is that agents have to figure out what maximizes utility, not predict what they will do because the self-reference causes problems.
E.g., we don’t want a calculator that outputs “whatever I output for 2+2” we want a calculator to output the answer to 2+2. The former is true no matter what the calculator outputs, the latter has a single answer. Similarly, there is only one action which maximizes utility (or at least a subset of all possible actions). But if an agent takes the action that it predicts it will take, it’s predictions are true by definition, so any action suffices.
I think real agents act as though they believe they have free will.
That means that they rate their own decisions to act as determining their actions, and advice from others about how they think they are going to act as being attempts to manipulate them. Another agent encouraging you to behave in a particular way isn’t usually evidence you should update on, it’s a manipulation attempt—and agents are smart enough to know the difference.
Are there circumstances under which you should update on such evidence? Yes, if the agent is judged to be both knowledgeable and trustworthy—but that is equally true if you employ practically any sensible decision process.
Re: if an agent takes the action that it predicts it will take, it’s predictions are true by definition, so any action suffices.
Agents do take the actions they predict they will take—it seems like a matter of fact to me. However, that’s not the criteria they use as the basis for making their predictions in the first place. I didn’t ever claim it was—such a claim would be very silly.
Indeed. You originally wrote:
You language is somewhat vague here, which is why EY clarified.
That was my immediate thought regarding puzzle piece 4. To say “X could happen” is just to say “I am uncertain about X, or I don’t have sufficient information to rule X out”. The impossible (e.g., for me) is what I can rule out; the possible is what I can’t. People talking about what’s really, really possible and impossible are just talking about what they believe the closest-to-perfect (but still imperfect) agent could know.
I’ve noticed that, on the few occasions I’ve taught genuine beginning-beginners. Never thought of it in that many words, but yeah. And the analogy to beginning rationality students, including 50-year-old scientists making up their own religions, is obvious and important. People starting out in math are operating in “sounds nice” mode, symbols with no consequences but their poetic resonance; and if you challenge their poetry they act all indignant, “Why’s yours better than mine?” 50-year-old religious scientists never leave that mode.
This resonated with me also. I tutored an at-best remedial high school student in geometry, and despite making lots of progress, could scarcely be talked out of really bad proofs.
“Look at it! It’s a right angle.” “Is it labeled as a right angle?” “No, but the one right above it is, and they look just alike!”
Is there a specific example of “50-year-old scientists making up their own religions” that you’re thinking of?
Maybe Steven Jay Gould’s nonoverlapping magisteria?
Tipler, too.
did you have anyone in mind?
In contrast to 30+ year-old rationalists justifying ethical behavior (“one-boxing”) on the grounds that they could be in a simulation run by someone trying to decide whether to defect or cooperate with them in the overworld?
Eliezer: “50-year-old scientists making up their own religions”
Silas: “In contrast to 30+ year-old rationalists justifying”
Eliezer is not yet 30. He’ll turn thirty in a few days, though.
Clearly this is grounds for another Overcoming Bias Bay Area Meetup. Meetup! Meetup!
I didn’t mean to refer to Eliezer_Yudkowsky. I just meant that if you put together a lot of the Newcomb and Simulation Argument theorizing, you get something quite similar to currently-existing religions. I was going to make it into a top-level post with all the parts spelled out, but figured it wouldn’t be welcome here.
The comment you responded to is the best one-sentence summary I can give though.
If we learn we are in a world that rewards two-boxing with more utility than one-boxing, “one-boxers” two-box and “two boxers” two-box.
If we learn we are in a world that rewards one-boxing with more utility that two-boxing, “one-boxers” one box and “two-boxers” two-box.
We do not assume we are in either such world. Making up your own atheism consisting of “don’t do the unjustified thing” isn’t the same as making up your own religion by poorly justifying the unjustified thing.
A specialized not-obviously-CSA for a specific problem can be better than any known CSA. Is it useful to model array-sorting algorithms as incrementally increasing some kind of “utility functions”? Shouldn’t you narrow the problem domain a bit, for your statement to hold? But if we narrow it in the obvious way, we get tree-search with heuristics and there you have your answers nicely laid out mathematically.
Please exhibit a model agent (however simple) that can logically arrive at such a prediction, and then experience some kind of paradox/problem because of it. I say there’s no way: the former makes the latter impossible.
I don’t immediately see what the problem is with considering ultimately impossible choices. Perhaps considering a concrete example would be useful in triangulating towards a proper understanding.
Let’s suppose I have a function F(x) and suppose the domain of x of interest to me is {-1, 0, 10}. I would like to choose x to maximize F.
My choices are x1=-1, x2=0 and x3=10. I “consider” each choice by calculating F(x) and I choose the one that maximizes F.
I would say that x1,x2 and x3 are all choices because I compared them all in order to make my (deterministic) final choice. There is nothing problematic here, so I must delve deeper...
Perhaps the problem is with the calculation of F(x1), F(x2) and F(x3). In real life, you can’t calculate F(x) because doing so would require already choosing x, so you can only simulate what F(x) would give you. So here it seems necessary to make a distinction between F(x) and Fs(x), where Fs(x) is a model of F(x) that you can use to simulate what F(x) would give.
Thinking about what “would” happen “if you chose” x1 means calculating Fs(x1) -- not F(x1), because calculating F(x1) means choosing F(x1).
So maybe the naive realist is confusing Fs(x) and F(x)?
I think some concreteness might be useful here. When I write code (no pretense at AI here), I often write algorithms that take different actions depending on the circumstances. I can’t recall a time when I collected possible steps, evaluated them, and executed the possibility with the highest utility. Instead I, as the programmer, attempt to divide the world into disjoint possibilities, write an evaluation procedure that will distinguish between them (if-then-else, or using OO I ensure that the right kind of object will be acting at the time), and design the code so that it will take a specific action that I expected would make sense for that context when that is the path chosen. There’s little of “could” or “should” here.
On the other hand, when I walk into the kitchen thinking thoughts of dessert, I generate possibilities based on my recollection of what’s in the fridge and the cupboards or sometimes based on a search of those locations. I then think about which will taste better, which I’ve had more recently, which is getting old and needs to be used up, and then pick one (without justifying the choice based on the evaluations.) There seems to be lots of CSA going on here, even though it seems like a simple, highly constrained problem area.
When human chess masters play, they retain more could-ness in their evaluations if they consider the possibility of not making the “optimal” move in order to psych out their opponents. I don’t know whether the chess-playing automatons consider those possibilities. Without it, you could say they are constrained to make the move that leaves them in the best position according to their evaluation metric. So even though they do explicitly evaluate alternatives, they have a single metric for making a choice. The masters I just described have multiple metrics and a vague approach to combining them, but that’s the essence of good game playing.
Bottom line? When I’m considering a big decision, I want to leave more variables open, to simulate more possible worlds and the consequences of my choices. When I’m on well-trodden ground, I hope for an optimized decision procedure that knows what to do and has simple rules that allow it to determine which pre-analyzed direction is the right one. The reason we want AIs to be open in this way is that we’re hoping they have the breadth of awareness to tackle problems that they haven’t explicitly been programmed for. I don’t think you (the programmer) can leave out the could-ness unless you can enumerate the alternative actions and program in the relevant distinctions ahead of time.
Warning: grouchiness follows.
Actually, I made the same criticism of that category, except in more detail. Was that acausal, or am I just more worthy of reviewing your drafts?
And your response in the footnote looks like little more than, “don’t worry, you’ll get it some day, like schoolkids and fractions”. Not helpful.
Excuse me, isn’t this just the classical “rational agent” model that research has long since refuted? For one thing, many actions people perform are trivially impossible to interpret this way (in the sense of your diagram), given reaction times and known computational properties of the brain. That is, the brain doesn’t have enough time to form enough distinct substates isomorphic to several human-like responses, then evaluate them, then compare the evaluations.
For another, the whole heuristics and biases literature repeated ad infinitum on OB/LW.
Finally, even when humans do believe they’re evaluating several choices looking for the best payoff (per some multivariable utility function), what really happens is that they pick one quickly based on “gut instinct”—meaning some heuristic, good or bad—and then bend all conscious evaluation to favor it. In at least some laboratory settings, this is shown explicitly: the researchers can predict what the subject will do, and then the subject gives some plausible-sounding rationalization for why they did it.
(And if you say, “using heuristics is a kind of evaluation of alternatives”, then you’re again stretching the boundaries of the concept of a CSA wide enough to be unhelpful.)
There are indeed cases where people do truly consider the alternatives and make sure they are computing the actual consequences and the actual congruence with their actual values, but this is an art people have to genuinely work towards; it is not characteristic of general human action.
In any case, all of the above assumes a distinction I’m not convinced you’ve made. To count as a CSA, is it necessary that you be physically able to extract the alternatives under consideration (“Silas considered making his post polite, but assigned it low utility”)? Because the technology certainly doesn’t exist to do that on humans. Or is it only necessary that it be possible in principle? If the latter, you run back into the problem of the laws of physics being embedded in all parts of the universe:
I observe a pebble. Therefore, I know the laws of the universe. Therefore, I can compute arbitrary counterfactuals. Therefore, I compute a zero pebble-utility for everything the pebble “pebble-could” do, except follow the laws of physics.
Therefore, there is no “not-CSA” option.
If it is possible in principle, to physically extract the alternatives/utility assignments etc., wouldn’t that be sufficient to ground the CSA—non-CSA distinction, without running afoul of either current technological limitations, or the pebble-as-CSA problem? (Granted, we might not always know whether a given agent is really a CSA or not, but that doesn’t seem to obviate the distinction itself.)
Thanks for your reply.
For the purposes of the argument I was making, “possible in principle to physically extract” is the same as “possible in principle to extract”. For once you know the laws of physics, which supposedly you can learn from a pebble, you can physically extract data that is functionally equivalent to alternatives/utility assignments.
For example, our knowledge of thermodynamics and chemistry tells us that a chemical would go to a lower energy state (and perhaps release heat) if it could observe certain other chemicals (which we call “catalysts”). It is our knowledge of science that justifies saying that there is this lower energy state that it “has a tendency” to want to go to, which is an “alternative” lacking “couldness” in the same sense of the proposed CSAs.
Laying down rules for what counts as evidence that a body is considering alternatives, is messier than AnnaSalamon thinks.
Agreed. But I don’t think that means that it’s not possible to do so, or that there aren’t clear cases on either side of the line. My previous formulation probably wasn’t as clear as it should have been, but would the distinction seem more tenable to you if I said “possible in principle to observe physical representations of” instead of “possible in principle to physically extract”? I think the former better captures my intended meaning.
If there were a (potentially) observable physical process going on inside the pebble that contained representations of alternative paths available to it, and the utility assigned to them, then I think you could argue that the pebble is a CSA. But we have no evidence of that whatsoever. Those representations might exist in our minds once we decide to model the pebble in that way, but that isn’t the same thing at all.
On the other hand, we do seem to have such evidence for e.g. chess-playing computers, and (while claims about what neuroimaging studies have identified are frequently overstated) we also seem to be gathering it for the human brain.
Heh, I actually had a response half-written up to this position, until I decided that something like the comment I did make would be more relevant. So, let’s port that over...
The answer to your question is: yes, as long as you can specify what observations of the system (and you may of course include any physically-possible mode of entanglement) count as evidence for it having considered multiple alternatives.
This criterion, I think, is what AnnaSalamon should be focusing on: what does it mean for “alternative-consideration” to be embedded in a physical system? In such a limited world as chess, it’s easy to see the embedding. [Now begins what I hadn’t written before.] I think that’s a great example of what I’m wondering about: what is this possible class of intelligent algorithms that stands in contrast to CSAs? If there were a good chess computer that was not a CSA, what would it be doing instead?
You could imagine one, perhaps, that computes moves purely as a function of the current board configuration. If bishop here, more than three pawns between here, move knight there, etc.
The first thing to notice is that for the program to actually be good, it would require that some other process was able to find a lot of regularity to the search space, and compactly express it. And to find that regularity, it would have to interact with it. So, such a good “insta-evaluator” implicitly contains the result of previous simulations.
Arguably, this, rather than(?) a CSA is what humans (mostly) are. Throughout our evolutionary history, a self-replicating process iterated through a lot of experiences that told it what “does work” and “doesn’t work”. The way we exist today, just the same as in the case of chess above, implicitly contains a compression of previous evaluations of “does work” and “doesn’t work”, known as heuristics, which together guide our behavior.
Is a machine that acts purely this way, and without humans’ ability to consciously consider alternatives, what AnnaSalamon means by a non-CSA algorithm? Or would it include that too?
Perhaps it’s already been said, but isn’t there a temporal problem in this reasoning?
A CSA, while in the process of making its decision, does not yet know what its decision will be. Therefore it can evaluate any number of “coulds”, figuring out and caching the “woulds” before choosing its action, without causing any logical quandaries.
While evaluating a “could” it assumes for the purposes of the evaluation that it has evaluated everything already and this “could” was the chosen action.
Or did I completely miss the point?
EDIT: IOW, there can’t be a counter-factual until a “factual” exists, and a “factual” won’t exist until the decision process has completed...
In practice, it can; but formalizing this process requires formalizing logical uncertainty / impossible possible worlds, which is an unsolved problem.
First, I think you’re doing good, valuable stuff. In particular, the skeptism regarding naive realism.
However, your “puzzle piece 1” paragraph seems like it needs shoring up. Your puzzle piece 1 gives claims, at first, that CSAs are “common”, and then strengthens that to “ubiquity” in the last sentence. The concrete examples of CSAs given are “humans, some animals, and some human-created programs.” Couldn’t the known tendency for humans to confabulate explanations of their own reasoning processes explain both humans and human-created programs?
My suspicion is that chess has cast a long shadow over the history of artificial intelligence. Humans, confronted with the chess problem, naturally learn a CSA-like strategy of exploring the game tree, and can explain their strategy verbally. Humans who are skilled at chess are celebrated as skilled thinkers. Turing wrote about the possibility of a chess-playing machine in the context of artificial intelligence a long time ago. The game tree really does have Real Options and Real Choices. The counterfactuals involved in considering it do not seem philosophically problematic—there’s a bright line (the magic circle) to cross.
That being said, I agree that we need to start somewhere, and we can come back to this point later, to investigate agents which have other moderately plausible internal structures.
When playing chess, there is a strategy for cashing out counterfactuals of the form “If I make this move”, which involves considering the rules of chess, and the assumption that your opponent will make the best available move. The problem is to come up with a general method of cashing out counterfactuals that works in more general situations than playing chess. It does not work to just compute logical consequences because any conclusion can be derived from a contradiction. So a concept of counterfactuals should specify what other facts must be modified or ignored to avoid deriving a contradiction. The strategy used for chess achieves this by specifying the facts that you may consider.
I agree completely with your conclusion. However, your claim “any conclusion can be derived from a contradiction” is provocative. It is only true in classical logic—relevant logic does not have that problem.
Yes, but cash out what you mean. Physical chess programs do not have Physically Irreducible Choices, but do have real choices in some other sense. Specifying that sense, and why it is useful to think in terms of it, is the goal.
The way you capitalize “Physically Irreducible Choices” makes me think that you’re using a technical term. Let my try to unpack the gist as I understand it, and you can correct me.
You can shoehorn a Could/Would/Should kernel onto many problems. For example, the problem of using messy physical sensors and effectors to forage for sustanance in a real-world environment like a forest. Maybe the choices presented to the core algorithm include things like “lay low and conserve energy”, “shift to smaller prey”, “travel towards the sun”. These choices have sharp dividing lines between them, but there isn’t any such dividing line in the problem. There must something outside the Could/Would/Should kernel, actively and somewhat arbitrarily CONSTRUCTING these choices from continuousness.
In Kripke semantics, philosophers gesture at graph-shaped diagrams where the nodes are called “worlds”, and the edges are some sort of “accessibility” relation between worlds. Chess fits very nicely into those graph-shaped diagrams, with board positions corresponding to “worlds”, and legal moves corresponding to edges. Chess is unlike foraging in that the choices presented to the Could/Would/Should kernel are really out there in chess.
I hope this makes it clear in what sense chess, unlike many AI problems, does confront an agent with “Real Options”. Why would you say that chess programs do not have “Physically Irreducible Choices”? Is there any domain that you would say has “Physically Irreducible Choices”?
But at this point, you are thinking about semantics of a formal language, or of logical connectives, which makes the problem more crispy than the vague “could” and “would”. Surprisingly, the meaning of formal symbols is still in most cases reduced to informal words like “or” and “and”, somewhere down the road. This is the Tarskian way, where you hide the meaning in the intuitive understanding of the problem.
In order to formalize things, we need to push all the informality together into “undetermined words”. The standard examples are Euclidean “line” and “point”. It’s entirely possible to do proof theory and to write proofs entirely as a game of symbols. We do not need to pronounce the mountain /\ as “and”, nor the valley \/ as “or”. A formal system doesn’t need to be interpreted.
Your sentence “Surprisingly, the MEANING of formal symbols is still in most cases reduced to informal words like “or” and “and” somewhere down the road.” seems to hint at something like “Surprisingly, formal symbols are FUNDAMENTALLY based on informal notions.” or “Surprisingly, formal symbols are COMPRISED OF informal notions.”—I will vigorously oppose these implications.
We step from the real world things that we value (e.g. stepper motors not banging into things) into a formal system, interpreting it (e.g. a formal specification for correct motion). (Note: formalization is never protected by the arguments regarding the formal system’s correctness.) After formal manipulations (e.g. some sort of refinement calculus), we step outward again from a formal conclusion to an informal conclusion (e.g. a conviction that THIS time, my code will not crash the stepper motors). (Note: this last step is also an unprotected step).
-
But since this is the decision process that produces the “happens”, both “happens” are the same “happens”. In other words, it reduces to:
Which is correct. Because the CSA deterministically chooses the best option, checking each action to see if it is best is synonymous with checking it to see if it is possible.
I’m not sure this fits. Do the animal examples all share a common ancestor that is also a CSA, or did CSA-ness evolve (and fixate) independantly, on multiple branches of the evolutionary tree?
If it only fixated once, and all other examples stemmed from that (including humans writing programs that are modeled after a part of our own decision-making process) then can it really be said to be common at all? It would still clearly be useful in some sense, or it wouldn’t have fixated that one time. But it’s not clear to me that it’s any more useful than some other algorithm from an unrelated branch.
It seems like we can simplify things a little bit by simply recognizing that “pick the largest utility from our final list” isn’t terribly complex, but it seems to be the whole of “should”. The interesting bit seems to be the function U(x), and the ability to generate the list of options in the first place—coming up with what we “could” do and evaluating it. Once you have an ordered-by-utility list of “coulds”, you probably have your answer :)
My response to some respondents’ question of why the agent needs the evaluation-of-options stage before acting is simple: the evaluation of options is part of the deterministic process which produces the action!
If the agent did not evaluate the options, it would be a different agent and thus act differently—possibly less optimally for its own utility function.
Isn’t this why we want to be rational?
(Apologies if I am missing the point!)
We find CSA’s in our actual world because it is possible for them to evolve to that point (see humans for proof). Anything more advanced (A friendly AI, for example, that doesn’t act like a human) takes actual planning, and as we see, that’s a difficult task, whose first stage requires a CSA or equivalent strength of intelligence. Humans, you see, don’t experience the halting problem for this main reason: They Don’t Halt. Most “coulds, shoulds, woulds”, happen in the animal’s spare time. A human has a long, long list of default actions which didn’t require planning. If a situation arises which is truly unique, a human has no particular attachment to that situation, having never experienced it before, and can think abstractly about it. Anything else is in some way linked to a default behavior (which “feels right”), enabling something to feel possible. What makes CSA’s so handy to have is that even if they don’t know exactly WHAT to do, they still DO something. Solve the world’s problems, when you are not busy eating, sleeping, attempting to mate. A Friendly AI is not necessarily a Satisfied AI. Perhaps the trick is to give the AGI the ability to make paperclips every once in a while. General includes paperclips, correct? Otherwise one is only trying to make a VERY advanced thermostat.
But since this is the decision process that produces the “happens”, both “happens” are the same “happens”. In other words, it reduces to:
Which is correct. Because the CSA deterministically chooses the best option, checking each action to see if is best is synonymous with checking it to see if it is possible.
If it helps with understanding, you can throw some quantum dice in so that Bob really does take all options (with probability epsilon/n) and before deciding where to throw the vast majority of the probability mass, he computes the expected utility of each real branch.