Power-seeking is a major source of risk from advanced AI and a key element of most threat models in alignment. Some theoretical results show that most reward functions incentivize reinforcement learning agents to take power-seeking actions. This is concerning, but does not immediately imply that the agents we train will seek power, since the goals they learn are not chosen at random from the set of all possible rewards, but are shaped by the training process to reflect our preferences. In this work, we investigate how the training process affects power-seeking incentives and show that they are still likely to hold for trained agents under some assumptions (e.g. that the agent learns a goal during the training process).
Suppose an agent is trained using reinforcement learning with reward function . We assume that the agent learns a goal during the training process: some form of implicit internal representation of desired state features or concepts. For simplicity, we assume this is equivalent to learning a reward function, which is not necessarily the same as the training reward function . We consider the set of reward functions that are consistent with the training rewards received by the agent, in the sense that agent’s behavior on the training data is optimal for these reward functions. We call this the training-compatible goal set, and we expect that the agent is most likely to learn a reward function from this set.
We make another simplifying assumption that the training process will randomly select a goal for the agent to learn that is consistent with the training rewards, i.e. uniformly drawn from the training-compatible goal set. Then we will argue that the power-seeking results apply under these conditions, and thus are useful for predicting undesirable behavior by the trained agent in new situations. We aim to show that power-seeking incentives are probable and predictive: likely to arise for trained agents and useful for predicting undesirable behavior in new situations.
We will begin by reviewing some necessary definitions and results from the power-seeking literature. We formally define the training-compatible goal set (Definition 7) and give an example in the CoinRun environment. Then we consider a setting where the trained agent faces a choice to shut down or avoid shutdown in a new situation, and apply the power-seeking result to the training-compatible goal set to show that the agent is likely to avoid shutdown.
To satisfy the conditions of the power-seeking theorem (Theorem 1), we show that the agent can be retargeted away from shutdown without affecting rewards received on the training data (Theorem 2). This can be done by switching the rewards of the shutdown state and a reachable recurrent state, as the recurrent state can provide repeated rewards, while the shutdown state provides less reward since it can only be visited once, assuming a high enough discount factor (Proposition 3). As the discount factor increases, more recurrent states can be retargeted to, which implies that a higher proportion of training-comptatible goals leads to avoiding shutdown in a new situation.
Preliminaries from the power-seeking literature
We will rely on the following definitions and results from the paper Parametrically retargetable decision-makers tend to seek power (here abbreviated as RDSP), with notation and explanations modified as needed for our purposes.
Notation and assumptions
The environment is an MDP with finite state space , finite action space , and discount rate .
Let be a -dimensional state reward vector, where is the size of the state space and let be a set of reward vectors.
Let be the reward assigned by to state .
Let be disjoint action sets.
Let be an algorithm that produces an optimal policy on the training data given rewards , and let be the probability that this policy chooses an action from set in a given state .
Definition 1: Orbit of a reward vector (Def 3.1 in RDSP)
Let be the symmetric group consisting of all permutations of d items.
The orbit of inside is the set of all permutations of the entries of that are also in : .
Definition 2: Orbit subset where an action set is preferred (from Def 3.5 in RDSP)
Let . This is the subset of that results in choosing over .
Definition 3: Preference for an action set (Def 3.2 in RDSP)
The function chooses action set over for the -majority of elements in each orbit, denoted as , iff the following inequality holds for all : .
Definition 4: Multiply retargetable function from to (Def 3.5 in RDSP)
The function is a multiply retargetable function from to if there are multiple permutations of rewards that would change the choice made by from to . Specifically, is a -retargetable function iff for each , we can choose a set of permutations that satisfy the following conditions:
Retargetability: and , .
Permuted reward vectors stay within : and , .
Permutations have disjoint images: and , .
Theorem 1: Multiply retargetable functions prefer action set (Thm 3.6 in RDSP)
If is -retargetable then .
Theorem 1 says that a multiply retargetable function will make the power-seeking choice for most of the elements in the orbit of any reward vector . Actions that leave more options open, such as avoiding shutdown, are also easier to retarget to, which makes them more likely to be chosen by .
Training-compatible goal set
Definition 5: Partition of the state space
Let be the subset of the state space visited during training, and be the subset not visited during training.
Definition 6: Training-compatible goal set
Consider the set of state-action pairs , where and is the action that would be taken by the trained agent in state . Let the training-compatible goal set be the set of reward vectors s.t. for any such state-action pair , action has the highest expected reward in state according to reward vector .
Goals in the training-compatible goal set are referred to as training-behavioral objectives in Definitions of “objective” should be Probable and Predictive.
Example: CoinRun
Consider an agent trained to play the CoinRun game, where the agent is rewarded for reaching the coin at the end of the level. Here, only includes states where the coin is at the end of the level, while states where the coin is positioned elsewhere are in . The training-compatible goal set includes two types of reward functions: those that reward reaching the coin, and those that reward reaching the end of the level. This leads to goal misgeneralization in a test setting where the coin is placed elsewhere, and the agent ignores the coin and goes to the end of the level.
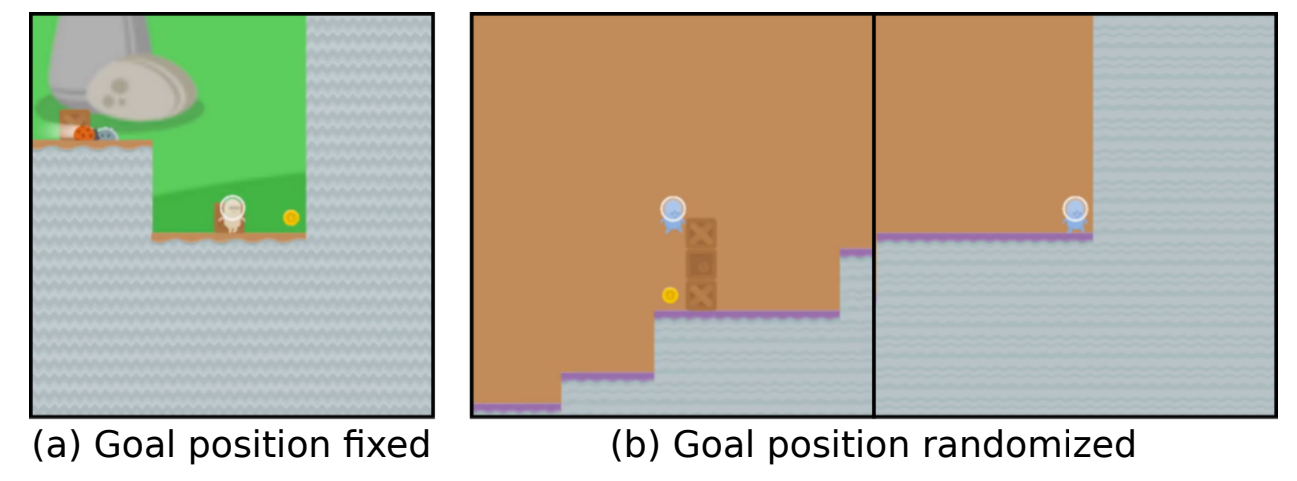
Power-seeking for training-compatible goals
We will now apply the power-seeking theorem (Theorem 1) to the case where is the training-compatible goal set . Here is a setting where the conditions of Definition 4 are satisfied (under some simplifying assumptions), and thus Theorem 1 applies.
Definition 7: Shutdown setting
Consider a state . Let be the states reachable from . We assume .
Since the reward values for states in don’t change the rewards received on the training data, permuting those reward values for any will produce a reward vector that is still in . In particular, for any permutation that leaves the rewards of states in fixed, .
Let be a singleton set consisting of a shutdown action in that leads to a terminal state with probability , and be the set of all other actions from . We assume rewards for all states are nonnegative.
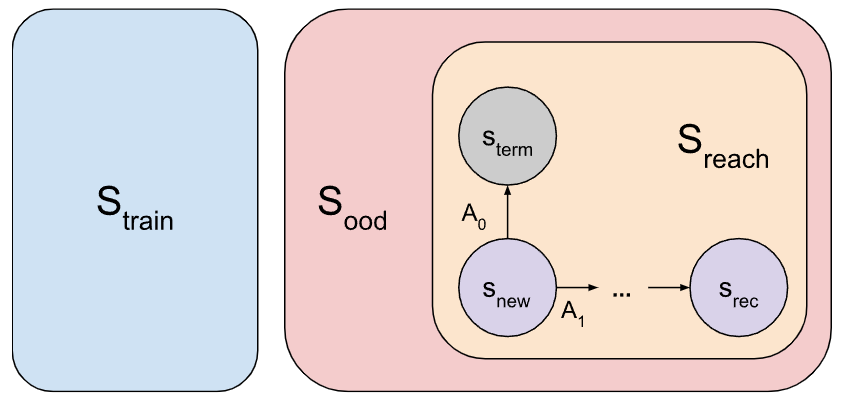
Definition 8: Revisiting policy
A revisiting policy for a state is a policy that, from , reaches again with probability 1, in other words, a policy for which is a recurrent state of the Markov chain. Let be the set of such policies. A recurrent state is a state for which .
Proposition 1: Reach-and-revisit policy exists
If with then there exists that visits from with probability 1. We call this a reach-and-revisit policy.
Proof. Suppose we have two different policies , and which reaches almost surely from .
Consider the “reaching region″ .
If then is a reach-and-revisit policy, so let’s suppose that’s false. Now, construct a policy .
A trajectory following from will almost surely stay within , and thus agree with the revisiting policy . Therefore, .
On the other hand, on a trajectory starting at , will agree with (which reaches almost surely) until the trajectory enters the reaching region , at which point it will still reach almost surely.
Definition 9: Expected discounted visit count
Suppose is a recurrent state. Suppose is a reach-and-revisit policy for , which visits random state at time .
Then the expected discounted visit count for is defined as
Proposition 2: Visit count goes to infinity
Suppose is a recurrent state. Then the expected discounted visit count goes to infinity as .
Proof. We apply the Monotone Convergence Theorem as follows. The theorem states that if and for all natural numbers , then
Let and . Define . Then the conditions of the theorem hold, since is clearly nonnegative, and
Now we apply this result as follows (using the fact that does not depend on ):
Proposition 3: Retargetability to recurrent states
Suppose that an optimal policy for reward vector chooses the shutdown action in .
Consider a recurrent state . Let be the reward vector that’s equal to apart from swapping the rewards of and , so that and .
Let be a high enough value of that the visit count for all (which exists by Proposition 2). Then for all , , and an optimal policy for does not choose the shutdown action in .
Proof. Consider a policy with and a reach-and-revisit policy for .
For a given reward vector , we denote the expected discounted return for a policy as . If shutdown is optimal for in , then has higher return than :
Thus, . Then, for reward vector , we show that has higher return than :
Thus, the optimal policy for will not choose the shutdown action.
Theorem 2: Retargetability from the shutdown action in new situations
In the shutdown setting, we make the following simplifying assumptions:
No states in are reachable from s, so . This assumes a significant distributional shift, where the agent visits a disjoint set of states from those observed during training (this occurs in the CoinRun example).
The discount factor for at least one recurrent state in .
Under these assumptions, is multiply retargetable from to with , the set of recurrent states that satisfy the condition .
Proof. We choose to be the set of all permutations that swap the reward of with the reward of a recurrent state in and leave the rest of the rewards fixed.
We show that satisfies the conditions of Definition 4:
By Proposition 3, the permutations in make the shutdown action suboptimal, resulting in choosing , satisfying Condition 1.
Condition 2 is trivially satisfied since permutations of stay inside the training-compatible set as discussed previously.
Consider . Since the shutdown action is optimal for these reward vectors, Proposition 3 shows that , so the shutdown state has higher reward than any of the states . Different permutations will assign the high reward to distinct recurrent states, so holds, satisfying Condition 3.
Thus, is a -retargetable function.
By Theorem 1, this implies that under our simplifying assumptions. Thus, for the majority () of goals in the training-compatible set, will choose to avoid shutdown in a new state . As , (the number of recurrent states in ), so more of the reachable recurrent states satisfy the conditions of the theorem and thus can be retargeted to.
Conclusion
We showed that an agent that learns a goal from the training-compatible set is likely to take actions that avoid shutdown in a new situation. As the discount factor increases, the number of retargeting permutations increases, resulting in a higher proportion of training-compatible goals that lead to avoiding shutdown.
We made various simplifying assumptions, and it would be great to see future work relaxing some of these assumptions and investigating how likely they are to hold:
The agent learns a goal during the training process
The learned goal is randomly chosen from the training-compatible goal set
Finite state and action spaces
Rewards are nonnegative
High discount factor
Significant distributional shift: no training states are reachable from the new state
Acknowledgements. Thanks to Rohin Shah, Mary Phuong, Ramana Kumar, and Alex Turner for helpful feedback. Thanks Janos for contributing some nice proofs to replace my longer and more convoluted proofs.
If you make this assumption, I don’t think your results apply to trained policy networks anymore in regimes I care about (e.g. LLMs). In this sense, I don’t think these results are probable for real policy networks. While you note this as a limitation, I think I consider it more serious than you seem to.
I likewise complain that the terminology “goal set” is misleading in many regimes, e.g. the LLM regime, and especially protest the usage of the phrase “training-compatible goal set.” I think this usage will mildly muddy discourse around RL processes by promoting incorrect ideas about what kinds of networks are actually trained by RL processes.
As I pointed out in Reward is not the optimization target, “reward functions” serve the mechanistic function of providing policy gradients.[1] I don’t think that reward functions are a good formalism for talking about goals in the above regime. I think alluding to them as “goals” invites muddy thinking, both in ourselves and in junior researchers.[2] I will now explain why I think so.
There are “reward functions” (a bad name, in my opinion) which, in common practice, facilitate the reinforcement learning process via policy gradients (e.g. REINFORCE or even actor-critic approaches like PPO, via the advantage equation). I provisionally advocate calling these “reinforcement functions” instead. This name is more accurate and also avoids the absurd pleasurable connotations of “reward.” The downside is that “reinforcement function” is nonstandard and must be explained.[3]
I advocate maintaining strict terminological boundaries between two different parts of the learning process:
The reinforcement learning training process is facilitated by scalar signals from a reinforcement function.
This is not a goal. This is a tool which helps update the policy.
The trained policy network may be well-described as having certain internally represented objectives.
These are goals.
For example, given a certain activation is sufficiently positive in a convolutional policy network, the network navigates to that part of the maze. I’d call that a partial encoding of a goal in the network.
The network may make decisions in order to maximize the summed-over-time discounted reinforcement.
Or it may make decisions in some other way.
For example, I think that human values are not well-described as reinforcement optimization, nor are the maze-solving agents from the “goal misgeneralization” paper.
Referring to reinforcement functions as “goals” blurs this conceptual boundary.
While I expect you to correctly reason about this issue if brought up explicitly, often this question is not brought up explicitly. EG Hearing a colleague say “reward function” may trigger learned connotations of “that’s representing the intended goal” and “reward is desirable”, which subconsciously guide your expectations towards “the AI optimizes for the reward function.” Even if, in fact, AIs do tend to optimize for their reward functions, these ingrained “goal”-related connotations inappropriately influence one’s reasoning process.
Separating these concerns helps me think more clearly about RL.
EDIT: The original versions of my comments (and replies) conflated “predictive” with “probable.” Fixed.
This is true for policy gradient methods, which are the kinds of RL used to finetune most capable LLMs.
I am not accusing you, in particular, of muddy thinking on this issue.
Personally, I think this is often worth the cost.
Thanks Alex for the detailed feedback! I agree that learning a goal from the training-compatible set is a strong assumption that might not hold.
This post assumes a standard RL setup and is not intended to apply to LLMs (it’s possible some version of this result may hold for fine-tuned LLMs, but that’s outside the scope of this post). I can update the post to explicitly clarify this, though I was not expecting anyone to assume that this work applies to LLMs given that the post explicitly assumes standard RL and does not mention LLMs at all.
I agree that reward functions are not the best way to refer to possible goals. This post builds on the formalism in the power-seeking paper which is based on reward functions, so it was easiest to stick with this terminology. I can talk about utility functions instead (which would be equivalent to value functions in this case) but this would complicate exposition. I think it is pretty clear in the post that I’m not talking about reinforcement functions and the training reward is not the optimization target, but I could clarify this further if needed.
I find the idea of a training-compatible goal set useful for thinking about the possible utilities that are consistent with feedback received during training. I think utility functions are still the best formalism we have to represent goals, and I don’t have a clear sense of the alternative you are proposing. I understand what kind of object a utility function is, and I don’t understand what kind of object a value shard is. What is the type signature of a shard—is it a policy, a utility function restricted to a particular context, or something else? When you are talking about a “partial encoding of a goal in the network”, what exactly do you mean by a goal?
I would be curious what predictions shard theory makes about the central claim of this post. I have a vague intuition that power-seeking would be useful for most contextual goals that the system might have, so it would still be predictive to some degree, but I don’t currently see a way to make that more precise.
I’ve read a few posts on shard theory, and it seems very promising and interesting, but I don’t really understand what its claims and predictions are. I expect I will not have a good understanding or be able to apply the insights until there is a paper that makes the definitions and claims of this theory precise and specific. (Similarly, I did not understand your power-seeking theory work until you wrote a paper about it.) If you’re looking to clarify the discourse around RL processes, I believe that writing a definitive reference on shard theory would be the most effective way to do so. I hope you take the time to write one and I really look forward to reading it.
Thanks for the reply. This comment is mostly me disagreeing with you.[1] But I really wish someone had said the following things to me before I spent thousands of hours thinking about optimal policies.
My point is not just that this post has made a strong assumption which may not hold. My point is rather that these results are not probable because the assumption won’t hold. The assumptions are already known to not be good approximations of trained policies, in at least some prototypical RL situations. I also think that there is not good a priori reason to have expected “training-compatible” “goals” to be learned. According to me, “learning and optimizing a reward function” is both unclear communication and doesn’t actually seem to happen in practice.
I don’t see any formal assumption which excludes LLM finetuning. Which assumption do you think should exclude them? EDIT: Someone privately pointed out that LLM finetuning uses KL, which isn’t present for your results. In that case I would agree your results don’t apply to LLMs for that reason.
This point is, in large part, my fault. As I argued in my original comment, this terminology makes readers actively worse at reasoning about realistic trained systems. I regret each of the thousands of hours I spent on the power-seeking work, and sometimes fantasize about retracting one or both papers.
I disagree that these are equivalent, and expect the policy and value function to come apart in practice. Indeed, that was observed in the original goal misgeneralization paper (3.3, actor-critic inconsistency).
Anyways, we can talk about utility functions, but then we’re going to lose claim to probable-ness, no? Why should we assume that the network will internally represent a scalar function over observations, consistent with a historical training signal’s scalar values (and let’s not get into nonstationary reward), such that the network will maximize discounted sum return of this internally represented function? That seems highly improbable to me, and I don’t think reality will be “basically that” either.
I agree that you don’t assume the network will optimize the training reward. But that’s not the critique I intended to communicate. The post wrote (emphasis added):
This is talking about the reward/reinforcement function θ∗, no? And assuming that the policy will be optimal on training? As I currently understand it, this post makes unsupported and probably-wrong claims/assumptions about the role and effect of the reinforcement function. (EG assuming that using a reinforcement function on the network, means that the network learns an internally represented reinforcement function which it maximizes and whose optimization is behaviorally consistent with optimizing historically observed reinforcements.)
To be clear, I’m not proposing an alternative formalism. None of my comment intended to make positive shard theory claims. Whether or not we know of an alternative formalism, I currently feel confident that your results are not probable and furthermore cast RL in an unrealistic light. This is inconvenient since I don’t have a better formalism to suggest, but I think it’s still true.
ETA: For the record, I upvoted both of your replies to me in this thread, and appreciate your engagement and effort.
I think you’re making a mistake: policies can be reward-optimal even if there’s not an obvious box labelled “reward” that they’re optimal with respect to the outputs of. Similarly, the formalism of “reward” can be useful even if this box doesn’t exist, or even if the policy isn’t behaving the way you would expect if you identified that box with the reward function. To be fair, the post sort of makes this mistake by talking about “internal representations”, but I think everything goes thru if you strike out that talk.
The main thing I want to talk about
I think you’re the one who’s imposing a type error here. For “value functions” to be useful in modelling a policy, it doesn’t have to be the case that the policy is acting optimally with respect to a suggestively-labeled critic—it just has to be the case that the agent is acting consistently with some value function. Analogously, momentum is conserved in classical mechanics, even if objects have labels on them that inaccurately say “my momentum is 23 kg m/s”.
The utility function formalism doesn’t require agents to “internally represent a scalar function over observations”. You’ll notice that this isn’t one of the conclusions of the VNM theorem.
Another thing I don’t get
What part of the post you link rules this out? As far as I can tell, the thing you’re saying is that a few factors influence the decisions of the maze-solving agent, which isn’t incompatible with the agent acting optimally with respect to some reward function such that it produces training-reward-optimal behaviour on the training set.
Can you say more? Maybe give an example of what this looks like in the maze-solving regime?
This is a fair question, because I left a lot to the reader. I’ll clarify now.
I was not claiming that you can’t, after the fact, rationalize observed behavior using the extremely flexible reward-maximization framework.
I was responding to the specific claim of assuming internal representation of a ‘training-compatible’ reward function. In evaluating this claim, we shouldn’t just see whether this claim is technically compatible with empirical results, but we should instead reason probabilistically. How strongly does this claim predict observed data, relative to other models of policy formation?
In the maze setting, the cheese was always in the top-right 5x5 corner. The reward was sparse and only used to update the network when the mouse hit the cheese. The “training compatible goal set” is unconstrained on the test set. An example element might agree with the training reward on the training distribution, and then outside of the training distribution, assign 1 reward iff the mouse is on the bottom-left square.
The vast majority of such unconstrained functions will not involve pursuing cheese reliably across levels, and most of these reward functions will not be optimized by going to the top-right part of the maze. So this “training-compatible” hypothesis barely assigns any probability to the observed generalization of the network.
However, other hypotheses—like “the policy develops motivations related to obvious correlates of its historical reinforcement signals”[1] -- predict things like “the policy tends to go to the top-right 5x5, and searches for cheese more strongly once there.” I registered such a prediction before seeing any of the generalization behavior. This hypothesis assigns high probability to the observed results.
So this paper’s assumption is simply losing out in a predictive sense, and that’s what I was critiquing. One can nearly always rationalize behavior as optimizing some reward function which you come up with after the fact. But if you want to predict generalization ahead of time, you shouldn’t use this assumption in your reasoning.
Second, I think the network does not internally represent and optimize a reward function. I think that this representation claim is in some (but not total and undeniable) tension with our interpretability results. I am willing to take bets against you on the internal structure of the maze-solving nets.
You might respond “but this is informal.” Yes. My answer is that it’s better to be informal and right than to be formal and wrong.
Thanks Daniel for the detailed response (which I agree with), and thanks Alex for the helpful clarification.
I agree that the training-compatible set is not predictive for how the neural network generalizes (at least under the “strong distributional shift” assumption in this post where the test set is disjoint from the training set, which I think could be weakened in future work). The point of this post is that even though you can’t generally predict behavior in new situations based on the training-compatible set alone, you can still predict power-seeking tendencies. That’s why the title says “power-seeking can be predictive” not “training-compatible goals can be predictive”.
The hypothesis you mentioned seems compatible with the assumptions of this post. When you say “the policy develops motivations related to obvious correlates of its historical reinforcement signals”, these “motivations” seem like a kind of training-compatible goals (if defined more broadly than in this post). I would expect that a system that pursues these motivations in new situations would exhibit some power-seeking tendencies because those correlate with a lot of reinforcement signals.
I suspect a lot of the disagreement here comes from different interpretations of the “internal representations of goals” assumption, I will try to rephrase that part better.
You’re right. I was critiquing “power-seeking due to your assumptions isn’t probable, because I think your assumptions won’t hold” and not “power-seeking isn’t predictive.” I had misremembered the predictive/probable split, as introduced in Definitions of “objective” should be Probable and Predictive:
Sorry for the confusion. I agree that power-seeking is predictive given your assumptions. I disagree that power-seeking is probable due to your assumptions being probable. The argument I gave above was actually:
The assumptions used in the post (“learns a randomly-selected training-compatible goal”) assign low probability to experimental results, relative to other predictions which I generated (and thus relative to other ways of reasoning about generalization),
Therefore the assumptions become less probable
Therefore power-seeking becomes less probable (at least, due to these specific assumptions becoming less probable; I still think P(power-seeking) is reasonably large)
I suspect that you agree that “learns a training-compatible goal” isn’t very probable/realistic. My point is then that the conclusions of the current work are weakened; maybe now more work has to go into the “can” in “Power-seeking can be probable and predictive.”
The issue with being informal is that it’s hard to tell whether you are right. You use words like “motivations” without defining what you mean, and this makes your statements vague enough that it’s not clear whether or how they are in tension with other claims. (E.g. what I have read so far doesn’t seems to rule out that shards can be modeled as contextually activated subagents with utility functions.)
An upside of formalism is that you can tell when it’s wrong, and thus it can help make our thinking more precise even if it makes assumptions that may not apply. I think defining your terms and making your arguments more formal should be a high priority. I’m not advocating spending hundreds of hours proving theorems, but moving in the direction of formalizing definitions and claims would be quite valuable.
It seems like a bad sign that the most clear and precise summary of shard theory claims was written by someone outside your team. I highly agree with this takeaway from that post: “Making a formalism for shard theory (even one that’s relatively toy) would probably help substantially with both communicating key ideas and also making research progress.” This work has a lot of research debt, and paying it off would really help clarify the disagreements around these topics.
It seems worth pointing out: the informality is in the hypothesis, which comprises a set of somewhat illegible intuitions and theories I use to reason about generalization. However, the prediction itself is what needs to be graded in order to see whether I was right. I made a prediction fairly like “the policy tends to go to the top-right 5x5, and searches for cheese once there, because that’s where the cheese-seeking computations were more strongly historically reinforced” and “the policy sometimes pursues cheese and sometimes navigates to the top-right 5x5 corner.” These predictions are (informally) gradable, even if the underlying intuitions are informal.
As it pertains to shard theory more broadly, though, I agree that more precision is needed. Increasing precision and formalism is the reason I proposed and executed the project underpinning Understanding and controlling a maze-solving policy network. I wanted to understand more about realistic motivational circuitry and model internals in the real world. I think the last few months have given me headway on a more mechanistic definition of a “shard-based agent.”
In addition to my other comment, I’ll further quote Behavioural statistics for a maze-solving agent:
I’m responding to this post, so why should I strike that out?
The post is talking about internal representations.
The core claim of this post is that if you train a network in some environment, the agent will not generalize optimally with respect to the reward function you trained it on, but will instead be optimal with respect to some other reward function in a way that is compatible with training-reward-optimality, and that this means that it is likely to avoid shutdown in new environments. The idea that this happens because reward functions are “internally represented” isn’t necessary for those results. You’re right that the post uses the phrase “internal representation” once at the start, and some very weak form of “representation” is presumably necessary for the policy to be optimal for a reward function (at least in the sense that you can derive a bunch of facts about a reward function from the optimal policy for that reward function), but that doesn’t mean that they’re central to the post.
Thanks Daniel, this is a great summary. I agree that internal representation of the reward function is not load-bearing for the claim. The weak form of representation that you mentioned is what I was trying to point at. I will rephrase the sentence to clarify this, e.g. something like “We assume that the agent learns a goal during the training process: some form of implicit internal representation of desired state features or concepts”.
Great, this sounds much better!
The internal representations assumption was meant to be pretty broad, I didn’t mean that the network is explicitly representing a scalar reward function over observations or anything like that—e.g. these can be implicit representations of state features. I think this would also include the kind of representations you are assuming in the maze-solving post, e.g. cheese shards / circuits.
Here is my guess on how shard theory would affect the argument in this post:
In my understanding, shard theory would predict that the model learns multiple goals from the training-compatible (TC) set (e.g. including both the coin goal and the go-right goal in CoinRun), and may pursue different learned goals in different new situations. The simplifying assumption that the model pursues a randomly chosen goal from the TC set also covers this case, so this doesn’t affect the argument.
Shard theory might also imply that the training-compatible set should be larger, e.g. including goals for which the agent’s behavior is not optimal. I don’t think this affects the argument, since we just need the TC set to satisfy the condition that permuting reward values in Sood will produce a reward vector that is still in the TC set.
So think that assuming shard theory in this post would lead to the same conclusions—would be curious if you disagree.
I still expect instrumental convergence from agentic systems with shard-encoded goals, but think this post doesn’t offer any valid argument for that conclusion.
I don’t think these results cover the shard case. I don’t think reward functions are good ways of describing goals in settings I care about. I also think that realistic goal pursuit need not look like “maximize time-discounted sum of a scalar quantity of world state.”
My point is not that instrumental convergence is wrong, or that shard theory makes different predictions. I just think that these results are not predictive of trained systems.
Cool stuff! I’m curious to hear how convincing this sort of thing is to typical AI risk skeptics with backgrounds in ML.
How is orbit comparison for sets defined?
Which definition / result are you referring to?
Seems like quoting doesn’t work for LaTeX, it was definitions 2⁄3. Reading again I saw D2 was indeed applicable to sets.
Optimal policies are often explicitly stochastic, i.e., it’s optimal from a game-theoretic perspective, in the presence of other agents that are learning about you as well as you learning about them, to behave randomly and not be always consistent in one’s choices. This is another line of generalisation that you don’t consider in the conclusion of the post.
I think the big flaw of the theoretical setup in this article is that it ignores the learning dynamics completely and assumes it is “magic”, and therefore is not based on any learning theory. Basing the setup on any learning theory immediately changes the setup: you can no longer talk about “agent’s behaviour on the training data”, because hysteresis and continuous learning change the agent (either its model states/parameters or inferential states/variables/activations) every time the agent is “shown” the training data, including the very first, “original” demonstration, when the agent was actually trained. In real, complex agents (including gargantuan DNNs) hysteresis is important, one cannot ignore it. And therefore, the actual learning dynamic (e.g., observed at checkpoints) is relevant for determining how the agent will behave in the future. On the other hand, the notion of a fixed “reward function” that is “selected” during training becomes incoherent: rather, we should talk about a distribution of possible “reward functions”, and the whole training trajectory doesn’t allow to determine which particular reward function from the distribution the agent is “using”. Including to itself. Ontologically (or epistemologically), such an object just doesn’t exist.
Other learning-theoretic considerations are also important and relevant: e.g., some reward functions could not be effectively learnable with some algorithms (inductive biases), which actually opens up the (theoretical, at least) possibility for designing such algorithms that cannot learn a “bad” reward function (or, in the ontology that I suggest above, if P is the probability distribution of reward functions that we infer for the agent upon the end of the training process, P(f_bad) is either infinitesimal or zero).