Abstraction, Evolution and Gears
Meta: this project is wrapping up for now. This is the second of probably several posts dumping my thought-state as of this week.
It is an empirical fact that we can predict the day-to-day behavior of the world around us—positions of trees or buildings, trajectories of birds or cars, color of the sky and ground, etc—without worrying about the details of plasmas roiling in any particular far-away star. We can predict the behavior of a dog without having to worry about positions of individual molecules in its cells. We can predict the behavior of reinforced concrete without having to check it under a microscope or account for the flaps of butterfly wings a thousand kilometers away.
Our universe abstracts well: it decomposes into high-level objects whose internal details are approximately independent of far-away objects, given all of their high-level summary information.
It didn’t have to be this way. We could imagine a universe which looks like a cryptographic hash function, where most bits are tightly entangled with most other bits and any prediction of anything requires near-perfect knowledge of the whole system state. But empirically, our universe does not look like that.
Given that we live in a universe amenable to abstraction, what sorts of agents should we expect to evolve? What can we say about agency structure and behavior in such a universe? This post comes at the question from a few different angles, looking at different properties I expect evolved agents to display in abstraction-friendly universes.
Convergent Instrumental Goals
The basic idea of abstraction is that any variable X is surrounded by lots of noisy unobserved variables, which mediate its interactions with the rest of the universe. Anything “far away” from X—i.e. anything outside of those noisy intermediates—can only “see” some abstract summary information f(X). Anything more than a few microns from a transistor on a CPU will only be sensitive to the transistor’s on/off state, not its exact voltage; the gravitational forces on far-apart stars depend only on their total mass, momentum and position, not on the roiling of plasmas.
One consequence: if an agent’s goals do not explicitly involve things close to X, then the agent cares only about controlling f(X). If an agent does not explicitly care about exact voltages on a CPU, then it will care only about controlling the binary states (and ultimately, the output of the computation). If an agent does not explicitly care about plasmas in far-away stars, then it will care only about the total mass, momentum and position of those stars. This holds for any goal which does not explicitly care about the low-level details of X or the things nearby X.
This sounds like instrumental convergence: any goal which does not explicitly care about things near X itself will care only about controlling f(X), not all of X. Agents with different goals will compete to control the same things: high-level behaviors f(X), especially those with far-reaching effects.
Natural next question: does all instrumental convergence work this way?
Typical intuition for instrumental convergence is something like “well, having lots of resources increases one’s action space, so a wide variety of agents will try to acquire resources in order to increase their action space”. Re-wording that as an abstraction argument: “an agent’s accessible action space ‘far away’ from now (i.e. far in the future) depends mainly on what resources it acquires, and is otherwise mostly independent of specific choices made right now”.
That may sound surprising at first, but imagine a strategic video game (I picture Starcraft). There’s a finite world-map, so over a long-ish time horizon I can get my units wherever I want them; their exact positions don’t matter to my long-term action space. Likewise, I can always tear down my buildings and reposition them somewhere else; that’s not free, but the long-term effect of such actions is just having less resources. Similarly, on a long time horizon, I can build/lose whatever units I want, at the cost of resources. It’s ultimately just the resources which restrict my action space, over a long time horizon.
(More generally, I think mediating-long-term-action-space is part of how we intuitively decide what to call “resources” in the first place.)
Coming from a different angle, we could compare to TurnTrout’s formulation of convergent instrumental goals in MDPs. Those results are similar to the argument above in that agents tend to pursue states which maximize their long-term action space. We could formally define an abstraction on MDPs in which X is the current state, and f(X) summarizes the information about the current state relevant to the far-future action space. In other words, two states X with the same long-run action space will have the same f(X). “Power”, as TurnTrout defined it, would be an increasing function of f(X) - larger long-run action spaces mean more power. Presumably agents would tend to seek states with large f(X).
Modularity
Fun fact: biological systems are highly modular, at multiple different scales. This can be quantified and verified statistically, e.g. by mapping out protein networks and algorithmically partitioning them into parts, then comparing the connectivity of the parts. It can also be seen more qualitatively in everyday biological work: proteins have subunits which retain their function when fused to other proteins, receptor circuits can be swapped out to make bacteria follow different chemical gradients, manipulating specific genes can turn a fly’s antennae into legs, organs perform specific functions, etc, etc.
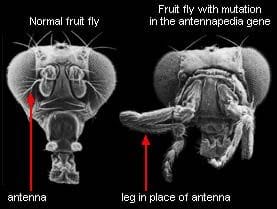
One leading theory for why modularity evolves is “modularly varying goals”: essentially, modularity in the organism evolves to match modular requirements from the environment. For instance, animals need to breathe, eat, move, and reproduce. A new environment might have different food or require different motions, independent of respiration or reproduction—or vice versa. Since these requirements vary more-or-less independently in the environment, animals evolve modular systems to deal with them: digestive tract, lungs, etc. This has been tested in simple simulated evolution experiments, and it works.
In short: modularity of the organism evolves to match modularity of the environment.
… and modularity of the environment is essentially abstraction-friendliness. The idea of abstraction is that the environment consists of high-level components whose low-level structure is independent (given the high-level summaries) for any far-apart components. That’s modularity.
Coming from an entirely different direction, we could talk about the good regulator theorem from control theory: any regulator of a system which is maximally successful and simple must be isomorphic to the system itself. Again, this suggests that modular environments should evolve modular “regulators”, e.g. organisms or agents.
I expect that the right formalization of these ideas would yield a theorem saying that evolution in abstraction-friendly environments tends to produce modularity reflecting the modular structure of the environment. Or, to put it differently: evolution in abstraction-friendly environments tends to produce (implicit) world-models whose structure matches the structure of the world.
Reflection
Finally, we can ask what happens when one modular component of the world is itself an evolved agent modelling the world. What would we expect this agent’s model of itself to look like?
I don’t have much to say yet about what this would look like, but it would be very useful to have. It would give us a grounded, empirically-testable outside-view correctness criterion for things like embedded world models and embedded decision theory. Ultimately, I hope that it will get at Scott’s open question “Does agent-like behavior imply agent-like architecture?”, at least for evolved agents specifically.
I think that there are some things that are sensitively dependant on other parts of the system, and we usually just call those bits random.
Suppose I had a magic device that returned the exact number of photons in its past lightcone. The answer from this box would be sensitively dependant on the internal workings of all sorts of things, but we can call the output random, and predict the rest of the world.
The flap of a butterflies wing might effect the weather in a months time. The weather is chaotic and sensitively dependant on a lot of things, but whatever the weather, the earths orbit will be unaffected (for a while, orbits are chaotic too on million year timescales)
We can make useful predictions (like planetary orbits, and how hot the planets will get) based just on the surface level abstractions like the brightness and mass of a star, but a more detailed models containing more internal workings would let us predict solar flares and supernova.
One key piece missing here: the parts we call “random” are not just sensitively dependent on other parts of the system, they’re sensitively dependent on many other parts of the system. E.g. predicting the long-run trajectories of billiard balls bouncing off each other requires very precise knowledge of the initial conditions of every billiard ball in the system. If we have no knowledge of even just one ball, then we have to treat all the long-run trajectories at random.
That’s why sensitive dependence on many variables matters: lack of knowledge of just one of them wipes out all of our signal. If there’s a large number of such variables, then we’ll always be missing knowledge of at least one, so we call the whole system random.
To expand on the billiard ball example, the degree of sensitivity is not always realised. Suppose that the conditions around the billiard table are changed by having a player stand on one side of it rather than the other. The difference in gravitational field is sufficient that after a ball has undergone about 7 collisions, its trajectory will have deviated too far for further extrapolation to be possible — the ball will hit balls it would have missed or vice versa. Because of exponential divergence, if the change were to move just the cue chalk from one edge of the table to another, the prediction horizon would be not much increased.
Do you have a source on that? My back-of-the-envelope says 7 is not enough. For 1 kg located 1 m away from 60 kg, gravitional force is on the order of 10^-9 N. IIRC, angular uncertainty in a billiards system roughly doubles with each head-on collision, so the exponential growth would only kick in around a factor of 128, which still wouldn’t be large enough to notice most of the time. (Though I believe the uncertainty grows faster for off-center hits, so that might be what I’m missing.)
I heard it a long long time ago in a physics lecture, but I since verified it. The variation in where a ball is struck is magnified by the ratio of (distance to the next collision) / (radius of a ball), which could be a factor of 30. Seven collisions gives you a factor of about 22 billion.
I also tried the same calculation with the motion of gas molecules. If the ambient gravitational field is varied by an amount corresponding to the displacement of one electron by one Planck length at a distance equal to the radius of the observable universe, I think I got about 30 or 40 collisions before the extrapolation breaks down.
Awesome. Thanks for the spot-check, I’ll probably use this as a dramatic example going forward.
I like this analysis. Whereas Seeking Power is Instrumentally Convergent in MDPs aimed to explain why seeking power is instrumentally convergent, this predicts qualitative properties of resource-hungry policies (“only cares about resource-relevant summary f(X) to the extent it affects long-term action spaces”). I think this frame also makes plain that most sensory reward functions don’t differentiate between “humans flourish + I have power” world histories, and “humans perish + I have power” world histories.
At this point, I ground my understanding of resources in the POWER(s) formulation (ability to achieve goals in general), and I think your take agrees with my model of that. Most goals we could have care more about the long-term action space, and so care about the stable and abstraction-friendly components of the environment which can widen that space (eg “resources”). Alternatively, resources are those things which tend to increase your POWER.
Mild progress on intentional stance for me: take a themostat. Realized you can count up the number of different temperatures the sensor is capable of detecting, number of states that the actuator can do in response (in the case of the thermostat only on/off) and the function mapping between the two. This might start to give some sense of how you can build up a multidimensional map out of multiple sensors and actuators as you do some sort of function combination.
Some parts of the universe are more amenable to abstraction than others—inside of a storm, the scope of it may be difficult to determine. From space, it may be trivial, up to a point. (Clarity from distance.)
Mostly, interconnection is limited by empty space everywhere.
The image this is a caption for isn’t showing up.
The low level details may be important as a means to an end.
Only given said resources, which is (presumably) the focus of said choices.
It seems this is more likely a result of how evolution works, i.e. modularity is good for refactoring.
The end in question being f(X), specifically. The agent will be indifferent between any X-values with the same f(X) - or, to put it differently, f(X) mediates the impact of X on the agent’s goals.
Similarly with the resources thing—the impact of current choices on far-future action space is mediated by resource quantities.
Thanks, this should be fixed now.