On martingales
Suppose we’re in Monaco (though not Monacan citizens) and itching for some roulette. We roll up to the Monte Carlo and bet $10 on black, but the ball stops on red. “No problem,” we think, “we just got unlucky.” We go to bet another $10, but pause for some quick math. We’re currently $10 in the hole; if we bet another $10, we’ll be down $20, and winning that bet will only bring us back to even. We realize that, in order to meet our original goal and leave the table $10 richer, we need to bet enough to recoup our losses, plus an extra $10, so instead we bet $20. Success! Congratulating ourselves on our brilliant strategy, we decide to spend the rest of the day milking it for all it’s worth, and by the evening we’re broke on the curb.
This sort of strategy is called a martingale, and it’s usually a bad idea, for a few reasons. For one, the Infinite Monkey theorem guarantees that, for any finite-size bankroll, we’ll eventually encounter a string of losses long enough that we can’t continue betting. For another, the size of our required bet grows at least exponentially in the number of consecutive losses, so the number of losses required to bankrupt us can be much lower than what one might expect. That said, the idea of the martingale has always kind of appealed to me (fortunately, I don’t live near Monaco), so I wanted to think about it a bit more quantitatively. Specifically, I wanted to know:
Given some level of risk tolerance and some betting strategy, how much profit can we make playing European roulette (which has slightly better odds than American), betting on black at 1:1 payout, using a martingale, assuming we don’t go bankrupt before hitting our risk threshold?
Let’s say we have dollars in our bank account, and we adopt the following strategy. On the first spin, we bet some fraction of our account size . If we lose, we bet to recoup our losses, plus an additional . We repeat this process until we win, in which case the bet resets to , or run out of money.
I’ll make a couple of simplifying assumptions, namely:
we neglect the growth of as we win
when the required bet size exceeds , we lose everything
Our bet size after losses is
We’d like to know the number of consecutive spins we can lose before going bankrupt , so we set this equation equal to and solve for . Unfortunately, this doesn’t have a nice solution in terms of elementary functions, but we can lower bound with and upper bound it with .
Solving for then gives
as a lower bound and
as an upper bound, where the comes from a switch from 0-indexing to 1-indexing. Let’s work with the upper bound for now. The probability of going broke each time we play the martingale (which I’ll call a ’’round”) is then
where is the probability of losing each spin, and for European roulette is .5135. Then the probability of going broke after $k$ rounds is
We have a risk tolerance ; we want the probability of going bankrupt to remain below . We solve for to find , the number of rounds we can play while remaining below our risk threshold:
If we successfully make it through these rounds, our winnings are
and our winnings as a fraction of our initial bankroll are
Let’s take a look at this function. Our winnings increase as increases; the higher the risk we can tolerate, the more we stand to win if we get lucky. The behavior in is a little trickier to intuit, but we can make some sense of it. The denominator increases as increases, so goes down; the more we bet each spin, the fewer rounds we can play before hitting our risk threshold. On the other hand, the numerator increases linearly in . Further complicating things is the embedded function, which will make the final overall function stepwise. Let’s plot it and see what it looks like:
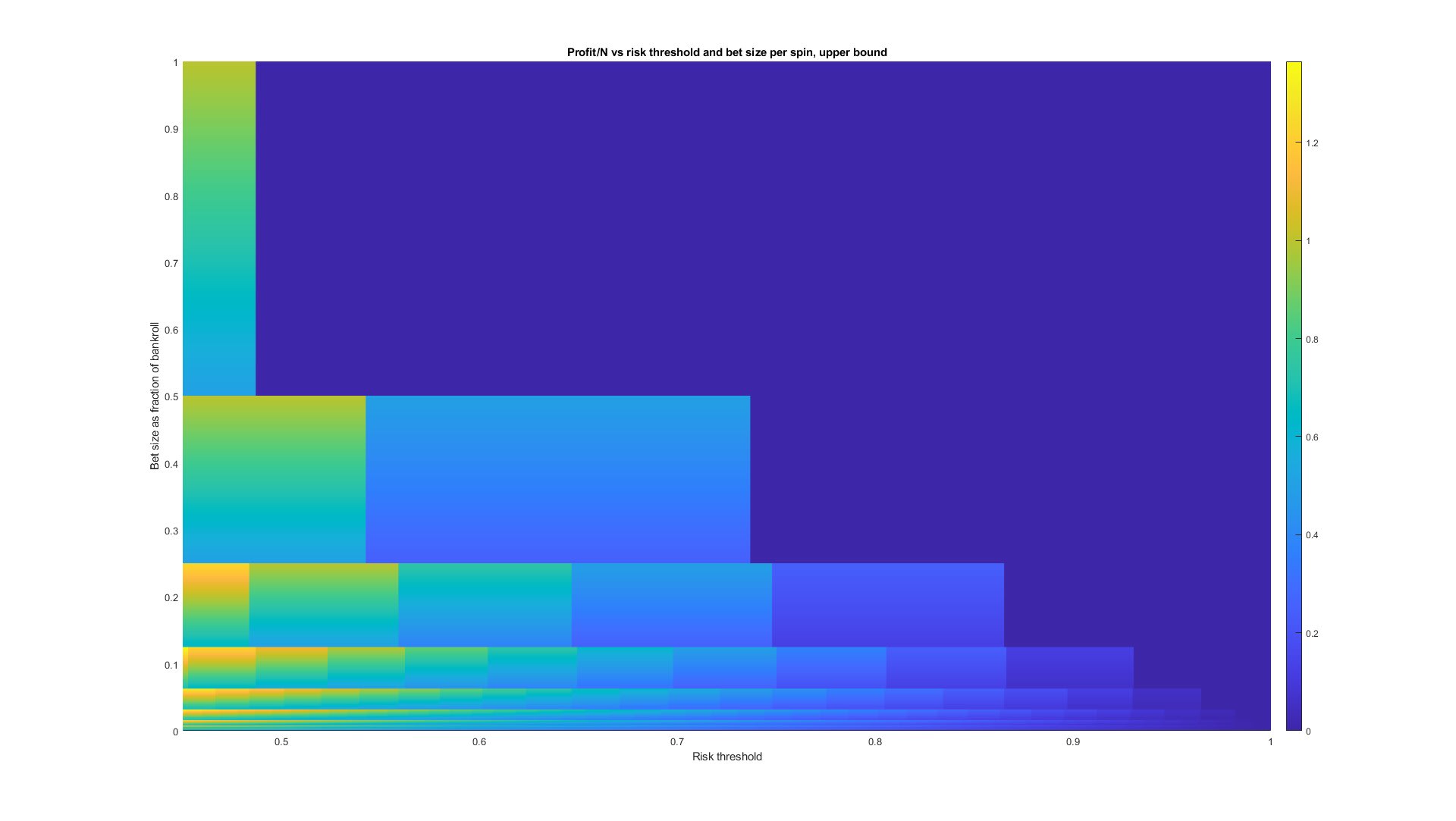
Nice! We see more or less the expected behavior, with the upper left corner representing betting everything on a single spin, and the upper right corner empty (there’s no way to e.g. bet 80% of your bankroll each spin and still keep your probability of winning above 90%). The lower left hand corner shows some interesting behavior; at first glance, it looks like we can win over 1.3 times our bankroll by betting about 3% per spin. Unfortunately, it’s easy to see that this can’t be right; in this case, our expected profit would be
and there’s no way to make money in expectation by playing a game with losing odds. In reality, this is a result of taking the upper bound mentioned earlier. Looking instead at the lower bound
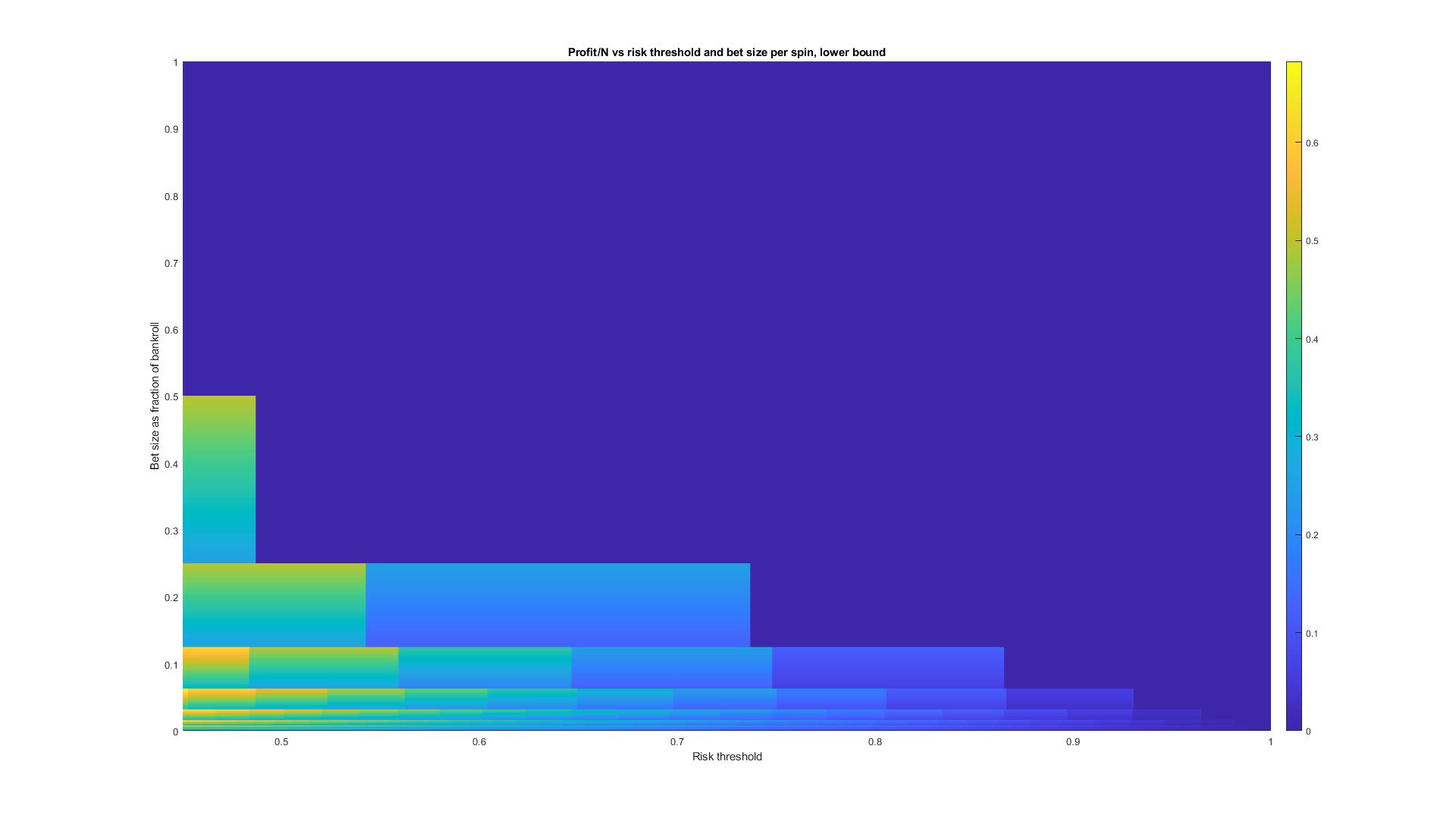
it’s clear that the martingale can’t do better than betting it all on black if we’re willing to accept a 51% chance of losing, and has negative expectation value everywhere. As rationalists, we don’t want to be playing negative expectation value games, so I suppose it’s time to give up on the martingale…
unless we jack up the probabilities by enough orders of magnitude that we can mumble something about Pascal’s Mugging and go back to spinning that wheel! So let’s do just that.
Suppose we’re Elon Musk and have dollars. We incur about a 1 in risk of death every time we hop on our jet, so we reason that we’re willing to risk our fortune at those odds. How much money can we make using the martingale with these parameters? We can’t solve the equation for , but we can fix and and plot our winnings:
By betting about 3e-8 of our fortune each round, we can make between ~$4500 and $9000 (taking the lower and upper bound, respectively) while staying below a 1 in risk of going broke! That covers about half of a first class flight from Austin to Monaco. Even worse, at that betting rate we can only play the martingale once before hitting our risk threshold, so we don’t even get to enjoy the free drinks. Better stake our billions elsewhere.
For a fixed, known, negative-expectation game, no betting strategy can change the mean outcome. It CAN change the distribution of outcomes, including the median and modal outcome. Well, depending on how you model the overall game (multiple iterations). One common analysis is “play until you win X or lose Y”, sometimes “or Z iterations”, but that makes generalization much harder, and is irrelevant most of the time.
In this approach, repeated Martingale bets of less than X is simply worse than Martingale starting at X. This is because your “bet handle”, the total money at risk, including re-betting winnings, is higher.
Much more interesting is postive-value bets, where you get to use logarithms. There’s a fair bit of LW discussion under the tag https://www.lesswrong.com/tag/kelly-criterion .
There are many plausible scenarios in which playing games with superficially negative outcomes is wise. The businessman who is facing bankruptcy unless he can deliver a million dollars to his creditors is rational to put his half-million on black.
Sure, one can always embed a game inside another one and so alter the overall expectation values how one likes. That said, we still only want to play the meta-game if it had positive expectation value, no?
Minor semantic quibble: I would say we always want positive expected utility, but how that translates into money/time/various intangibles can vary tremendously both situationally and from person to person.