DSLT 0. Distilling Singular Learning Theory
TLDR; In this sequence I distill Sumio Watanabe’s Singular Learning Theory (SLT) by explaining the essence of its main theorem—Watanabe’s Free Energy Formula for Singular Models—and illustrating its implications with intuition-building examples. I then show why neural networks are singular models, and demonstrate how SLT provides a framework for understanding phases and phase transitions in neural networks.
Epistemic status: The core theorems of Singular Learning Theory have been rigorously proven and published by Sumio Watanabe across 20 years of research. Precisely what it says about modern deep learning, and its potential application to alignment, is still speculative.
Acknowledgements: This sequence has been produced with the support of a grant from the Long Term Future Fund. I’d like to thank all of the people that have given me feedback on each post: Ben Gerraty, @Jesse Hoogland , @mfar, @LThorburn , Rumi Salazar, Guillaume Corlouer, and in particular my supervisor and editor-in-chief Daniel Murfet.
Theory vs Examples: The sequence is a mixture of synthesising the main theoretical results of SLT, and providing simple examples and animations that illustrate its key points. As such, some theory-based sections are slightly more technical. Some readers may wish to skip ahead to the intuitive examples and animations before diving into the theory—these are clearly marked in the table of contents of each post.
Prerequisites: Anybody with a basic grasp of Bayesian statistics and multivariable calculus should have no problems understanding the key points. Importantly, despite SLT pointing out the relationship between algebraic geometry and statistical learning, no prior knowledge of algebraic geometry is required to understand this sequence—I will merely gesture at this relationship. Jesse Hoogland wrote an excellent introduction to SLT which serves as a high level overview of the ideas that I will discuss here, and is thus recommended pre-reading to this sequence.
SLT for Alignment Workshop: This sequence was prepared in anticipation of the SLT for Alignment Workshop 2023 and serves as a useful companion piece to the material covered in the Primer Lectures.
Thesis: The sequence is derived from my recent masters thesis which you can read about at my website.
Developmental Interpretability: Originally the sequence was going to contain a short outline of a new research agenda, but this can now be found here instead.
Introduction
Knowledge to be discovered [in a statistical model] corresponds to a singularity.
...
If a statistical model is devised so that it extracts hidden structure from a random phenomenon, then it naturally becomes singular.
Sumio Watanabe
In 2009, Sumio Watanabe wrote these two profound statements in his groundbreaking book Algebraic Geometry and Statistical Learning where he proved the first main results of Singular Learning Theory (SLT). Up to this point, this work has gone largely under-appreciated by the AI community, probably because it is rooted in highly technical algebraic geometry and distribution theory. On top of this, the theory is framed in the Bayesian setting, which contrasts the SGD-based setting of modern deep learning.
But this is a crying shame, because SLT has a lot to say about why neural networks, which are singular models, are able to generalise well in the Bayesian setting, and it is very possible that these insights carry over to modern deep learning.
At its core, SLT shows that the loss landscape of singular models, the KL divergence , is fundamentally different to that of regular models like linear regression, consisting of flat valleys instead of broad parabolic basins. Correspondingly, the measure of effective dimension (complexity) in singular models is a rational quantity called the RLCT [1], which can be less than half the total number of parameters. This fact means that classical results of Bayesian statistics like asymptotic normality break down, but what Watanabe shows is that this is actually a feature and not a bug: different regions of the loss landscape have different tradeoffs between accuracy and complexity because of their differing information geometry. This is the content of Watanabe’s Free Energy Formula, from which the Widely Applicable Bayesian Information Criterion (WBIC) is derived, a generalisation of the standard Bayesian Information Criterion (BIC) for singular models.
With this in mind, SLT provides a framework for understanding phases and phase transitions in neural networks. It has been mooted that understanding phase transitions in deep learning may be a key part of mechanistic interpretability, for example in Induction Heads, Toy Models of Superposition, and Progress Measures for Grokking via Mechanistic Interpretability, which relate phase transitions to the formation of circuits. Furthermore, the existence of scaling laws and other critical phenomena in neural networks suggests that there is a natural thermodynamic perspective on deep learning. As it stands there is no agreed-upon theory that connects all of this, but in this sequence we will introduce SLT as a bedrock for a theory that can tie these concepts together.
In particular, I will demonstrate the existence of first and second order phase transitions in simple two layer feedforward ReLU neural networks which we can understand precisely through the lens of SLT. By the end of this sequence, the reader will understand why the following phase transition in the Bayesian posterior corresponds to a changing accuracy-complexity tradeoff of the different phases in the loss landscape:
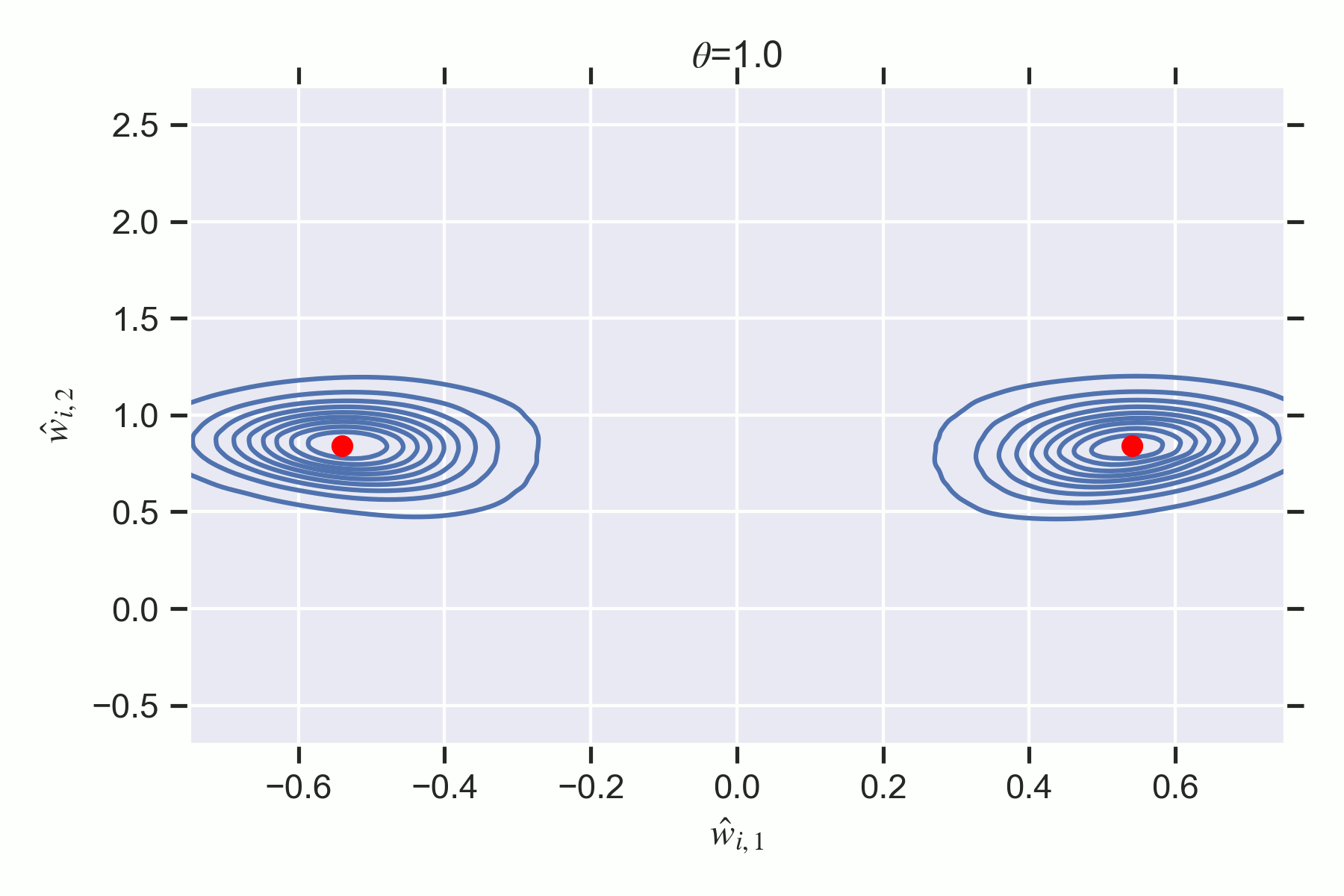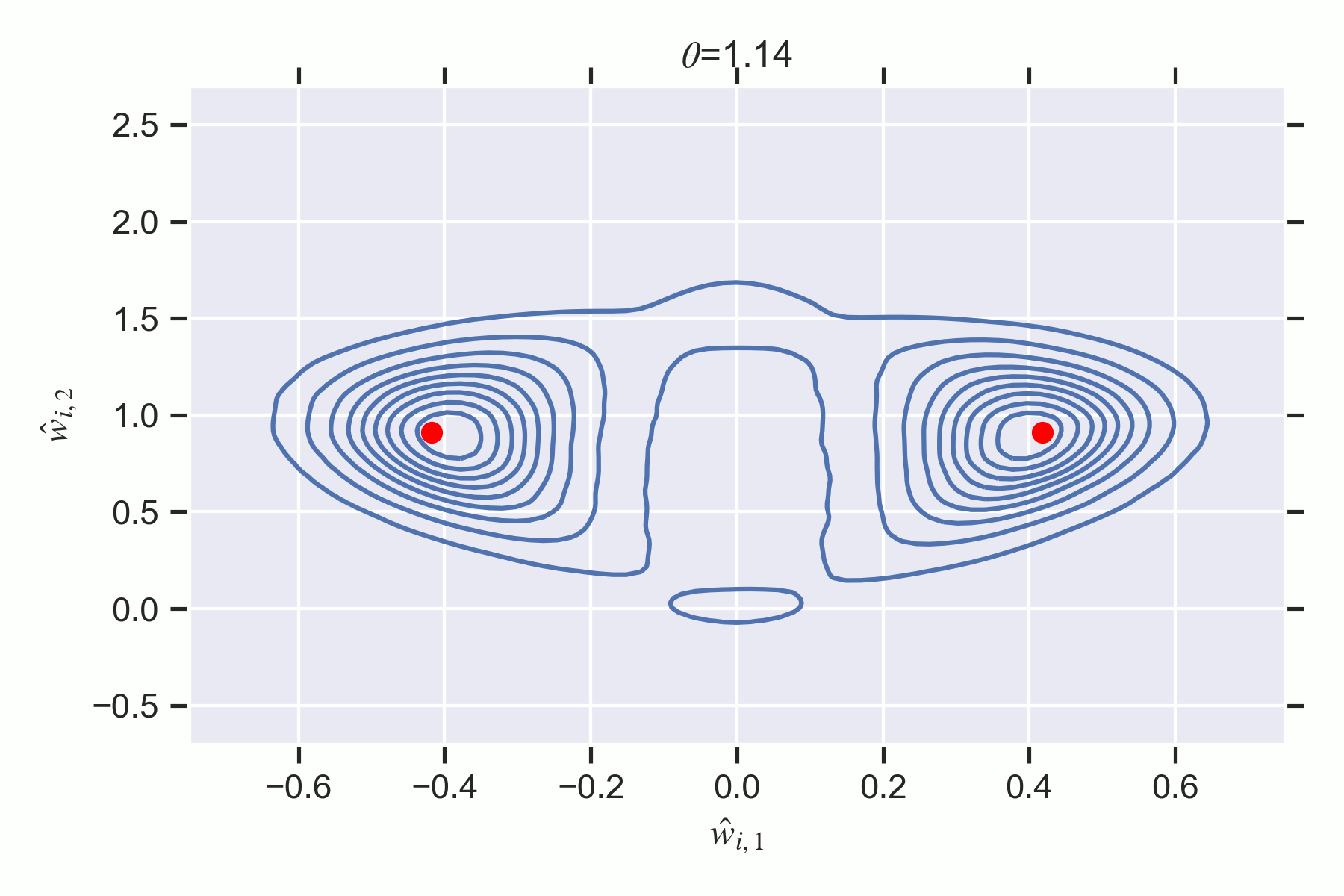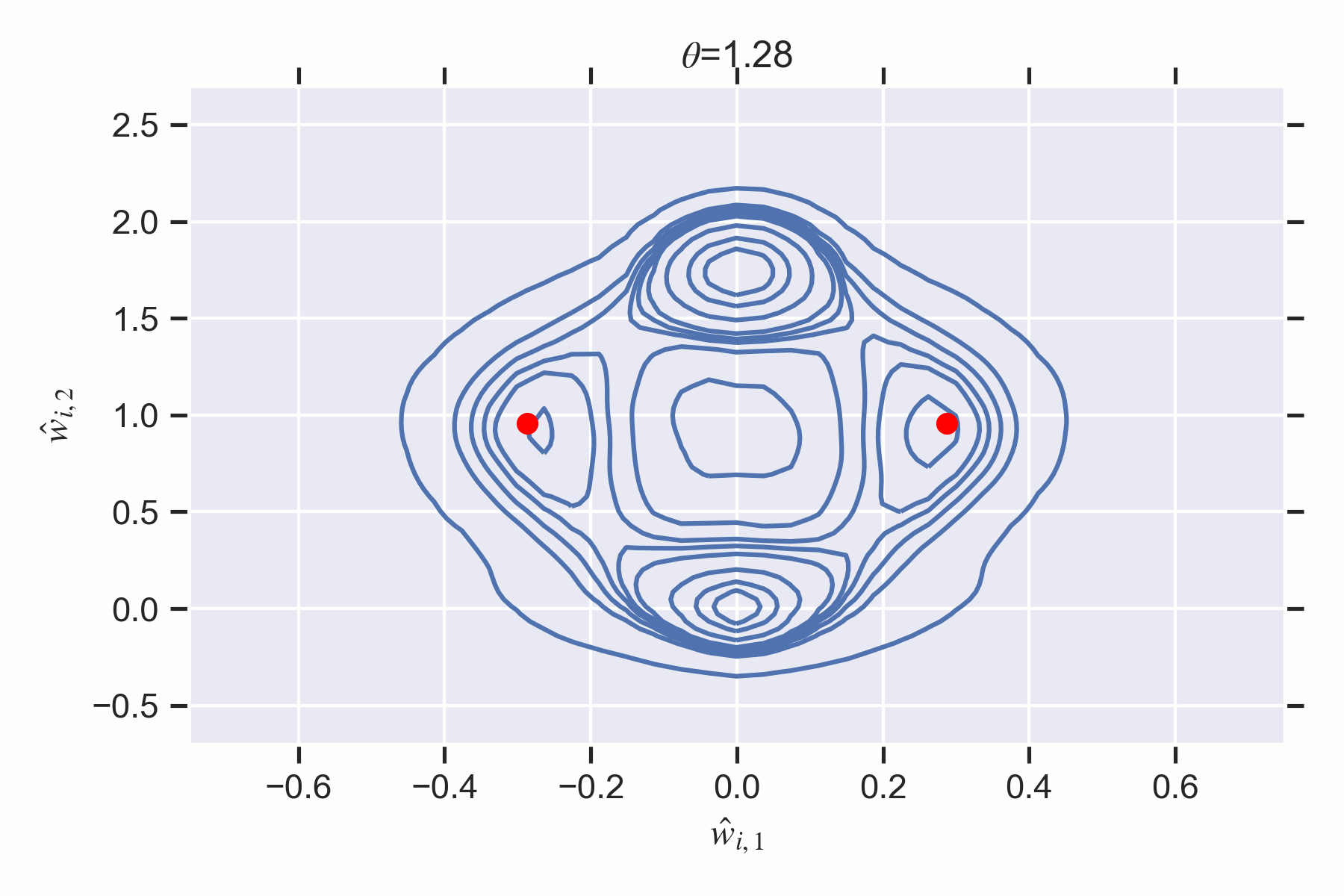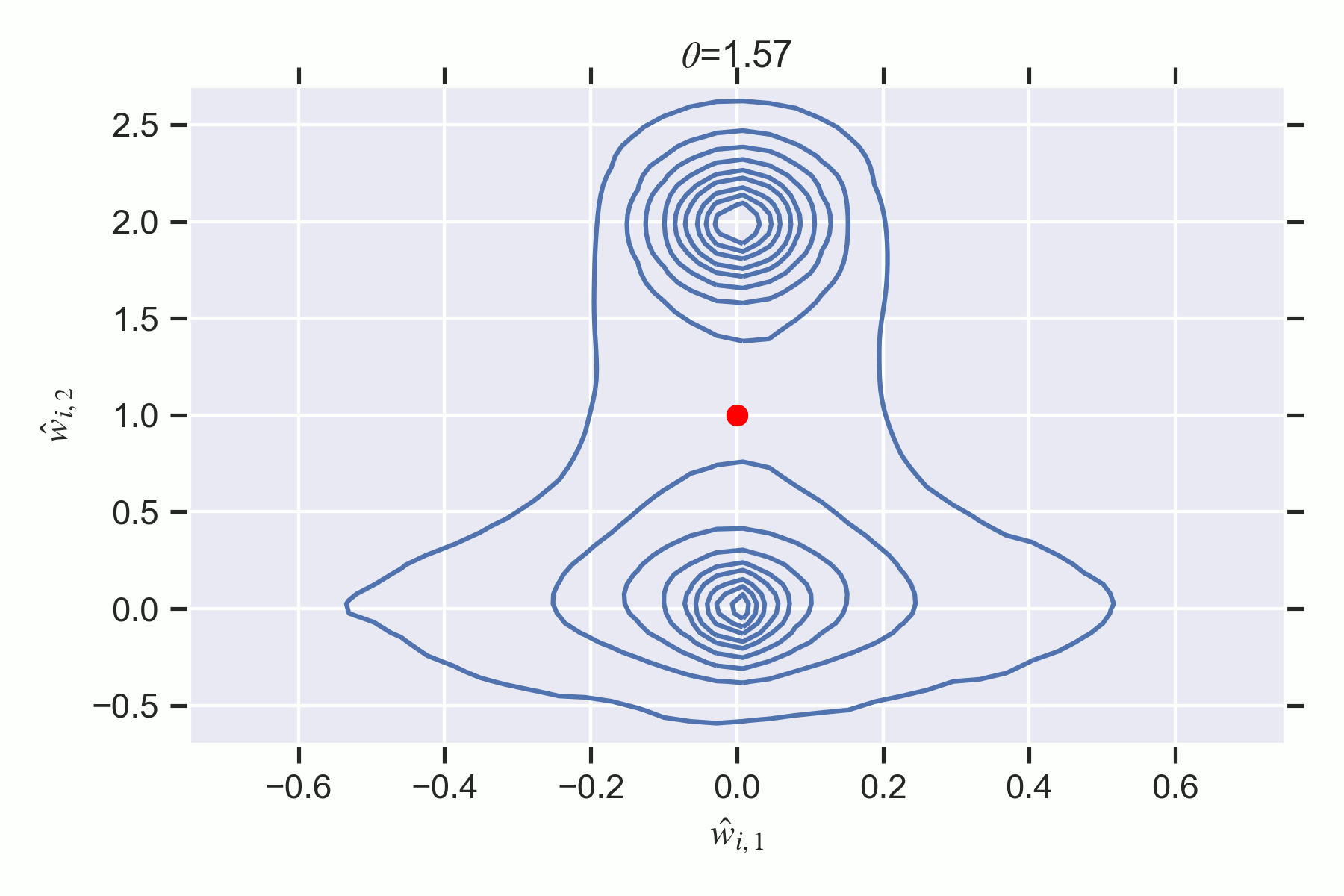
Key Points of the Sequence
To understand phase transitions in neural networks from the point of view of SLT, we need to understand how different regions of parameter space can have different accuracy-complexity tradeoffs, a feature of singular models that is not present in regular models. Here is the outline of how these posts get us there:
- DSLT 1. The RLCT Measures the Effective Dimension of Neural Networks
Singular models (like neural networks) are distinguished from regular models by having a degenerate Fisher information matrix, which causes classical results like asymptotic normality and the BIC to break down. Thus, singular posteriors do not converge to a Gaussian.
Because of this, the effective dimension of singular models is measured by a rational algebraic quantity called the RLCT , which can be less than half the dimension of parameter space.
DSLT 2. Why Neural Networks obey Occam’s Razor
The WBIC, which is a simplification of Watanabe’s Free Energy Formula, generalises the BIC for singular models, where complexity is measured by the RLCT and can differ across different regions of parameter space. (This is related to Bayesian generalisation error).
The WBIC can be interpreted as an accuracy-complexity tradeoff, showing that singular models obey a kind of Occam’s razor because:
As the number of datapoints , true parameters that minimise are preferred according to their RLCT.
Non-true parameters can still be preferred at finite if their RLCT is sufficiently small.
DSLT 3. Neural Networks are Singular
Neural networks are singular because there are many ways to vary their parameters without changing the function they compute.
I outline a full classification of these degeneracies in the simple case of two layer feedforward ReLU neural networks so that we can study their geometry as phases.
DSLT 4. Phase Transitions in Neural Networks
Phases in statistical learning correspond to a singularity of interest, each with a particular accuracy-complexity tradeoff. Phase transitions occur when there is a drastic change in the geometry of the posterior as some hyperparameter is varied.
I demonstrate the existence of first and second order phase transitions in simple two layer ReLU neural networks when varying the underlying true distribution.
(Edit: Originally the sequence was going to contain a post about SLT for Alignment, but this can now be found here instead, where a new research agenda, Developmental Interpretability, is introduced).
Resources
Though these resources are relatively sparse for now, expanding the reach of SLT and encouraging new research is the primary longterm goal of this sequence.
SLT Workshop for Alignment Primer
In June 2023, a summit, “SLT for Alignment”, was held, which produced over 20hrs of lectures. The details of these talks can be found here, with recordings found here.
Research groups
Research groups I know of working on SLT:
Prof. Sumio Watanabe’s research group at the Tokyo Institute of Technology.
Dr. Daniel Murfet and the Melbourne Deep Learning Group (MDLG), which runs a weekly seminar on metauni.
Literature
The two canonical textbooks due to Watanabe are:
[Wat09] The grey book: S. Watanabe Algebraic Geometry and Statistical Learning Theory 2009
[Wat18] The green book: S. Watanabe Mathematical Theory of Bayesian Statistics 2018
The two main papers that were precursors to these books:
[Wat07] S. Watanabe Almost All Learning Machines are Singular 2007 (paper)
[Wat13] S. Watanabe A Widely Applicable Bayesian Information Criterion 2013 (paper)
This sequence is based on my recent thesis:
[Car21] Liam Carroll’s MSc Thesis, October 2021 Phase Transitions in Neural Networks
MDLG recently wrote an introduction to SLT:
[Wei22] S. Wei, D. Murfet, M. Gong, H. Li , J. Gell-Redman, T. Quella “Deep learning is singular, and that’s good” 2022.
Other theses studying SLT:
[Lin11] Shaowei Lin’s PhD thesis, 2011, Algebraic Methods for Evaluating Integrals in Bayesian Statistics.
[War21] Tom Waring’s MSc thesis, October 2021, Geometric Perspectives on Program Synthesis and Semantics.
[Won22] Spencer Wong’s MSc thesis, May 2022, From Analytic to Algebraic: The Algebraic Geometry of Two Layer Neural Networks.
[Far22] Matt Farrugia-Roberts’ MCS thesis, October 2022, Structural Degeneracy in Neural Networks.
Other introductory blogs:
Jesse Hoogland’s blog posts: general intro to SLT, and effects of singularities on dynamics.
Edmund Lau’s blog Probably Singular.
- Growth and Form in a Toy Model of Superposition by (8 Nov 2023 11:08 UTC; 87 points)
- You’re Measuring Model Complexity Wrong by (11 Oct 2023 11:46 UTC; 82 points)
- Stagewise Development in Neural Networks by (20 Mar 2024 19:54 UTC; 80 points)
- The Low-Hanging Fruit Prior and sloped valleys in the loss landscape by (23 Aug 2023 21:12 UTC; 79 points)
- DSLT 1. The RLCT Measures the Effective Dimension of Neural Networks by (16 Jun 2023 9:50 UTC; 45 points)
- DSLT 4. Phase Transitions in Neural Networks by (24 Jun 2023 17:22 UTC; 30 points)
- DSLT 3. Neural Networks are Singular by (20 Jun 2023 8:20 UTC; 24 points)
- DSLT 2. Why Neural Networks obey Occam’s Razor by (18 Jun 2023 0:23 UTC; 20 points)
I’m kind of puzzled by the amount of machinery that seems to be going into these arguments, because it seems to me that there is a discrete analog of the same arguments which is probably both more realistic (as neural networks are not actually continuous, especially with people constantly decreasing the precision of the floating point numbers used in implementation) and simpler to understand.
Suppose you represent a neural network architecture as a map A:2N→F where 2={0,1} and F is the set of all possible computable functions from the input and output space you’re considering. In thermodynamic terms, we could identify elements of 2N as “microstates” and the corresponding functions that the NN architecture A maps them to as “macrostates”.
Furthermore, suppose that F comes together with a loss function L:F→R evaluating how good or bad a particular function is. Assume you optimize L using something like stochastic gradient descent on the function L with a particular learning rate.
Then, in general, we have the following results:
SGD defines a Markov chain structure on the space 2N whose stationary distribution is proportional to e−βL(A(θ)) on parameters θ for some positive constant β>0. This is just a basic fact about the Langevin dynamics that SGD would induce in such a system.
In general A is not injective, and we can define the “A-complexity” of any function f∈Im(A)⊂F as c(f)=Nlog2−log(|A−1(f)|). Then, the probability that we arrive at the macrostate f is going to be proportional to e−c(f)−βL(f).
When L is some kind of negative log likelihood, this approximates Solomonoff induction in a tempered Bayes paradigm insofar as the A-complexity c(f) is a good approximation for the Kolmogorov complexity of the function f, which will happen if the function approximator defined by A is sufficiently well-behaved.
Is there some additional content of singular value theory that goes beyond the above insights?
Edit: I’ve converted this comment to a post, which you can find here.
Edit: Originally the sequence was going to contain a post about SLT for Alignment, but this can now be found here instead, where a new research agenda, Developmental Interpretability, is introduced. I have also now included references to the lectures from the recent SLT for Alignment Workshop in June 2023.
I’m looking forward to both this series, and the workshop!
I think I (and probably many other people) would find it helpful if there was an entry in this sequence which was purely the classical story told in a way/with language which makes its deficiencies clear and the contrasts with the Watanabe version very easy to point out. (Maybe a −1 entry, since 0 is already used?)
The way I’ve structured the sequence means these points are interspersed throughout the broader narrative, but its a great question so I’ll provide a brief summary here, and as they are released I will link to the relevant sections in this comment.
In regular model classes, the set of true parameters W0 that minimise the loss K(w) is a single point. In singular model classes, it can be significantly more than a single point. Generally, it is a higher-dimensional structure. See here in DSLT1.
In regular model classes, every point on K(w) can be approximated by a quadratic form. In singular model classes, this is not true. Thus, asymptotic normality of regular models (i.e. every regular posterior is just a Gaussian as n→∞) breaks down. See here in DSLT1, or here in DSLT2.
Relatedly, the Bayesian Information Criterion (BIC) doesn’t hold in singular models, because of a similar problem of non-quadraticness. Watanabe generalises the BIC to singular models with the WBIC, which shows complexity is measured by the RLCT 2λ∈Q>0, not the dimension of parameter space d. The RLCT satisfies λ≤d2 in general, and λ=d2 when its regular. See here in DSLT2.
In regular model classes, every parameter has the same complexity d2. In singular model classes, different parameters w have different complexities λw according to their RLCT. See here in DSLT2.
If you have a fixed model class, the BIC can only be minimised by optimising the accuracy (see here). But in a singular model class, the WBIC can be minimised according to an accuracy-complexity tradeoff. So “simpler” models exist on singular loss landscapes, but every model is equally complex in regular models. See here in DSLT2.
With this latter point in mind, phase transitions are anticipated in singular models because the free energy is comprised of accuracy and complexity, which is different across parameter space. In regular models, since complexity is fixed, phase transitions are far less natural or interesting, in general.
Hi! I am in the process of reading this sequence and would love some supplemental lecture materials (particularly at the intersection of alignment research) and was very excited by the prospect of the lectures form the June summit, however the YouTube channels appears to 404 now. Is there somewhere else I can listen to these lectures?
Ah! Thanks for that—it seems the general playlist organising them has splintered a bit, so here is the channel containing the lectures, the structure of which is explained here. I’ll update this post accordingly.