Making DALL-E Count
Can DALL-E count? Does DALL-E’s counting ability depend on what it is counting? Let’s find out!
I only generate the images once and paste them in along with the prompt in quotations.
Numbers
“Zero”

“One”

“Two”

“Three”

“Four”

“Five”

“Six”

“Seven”
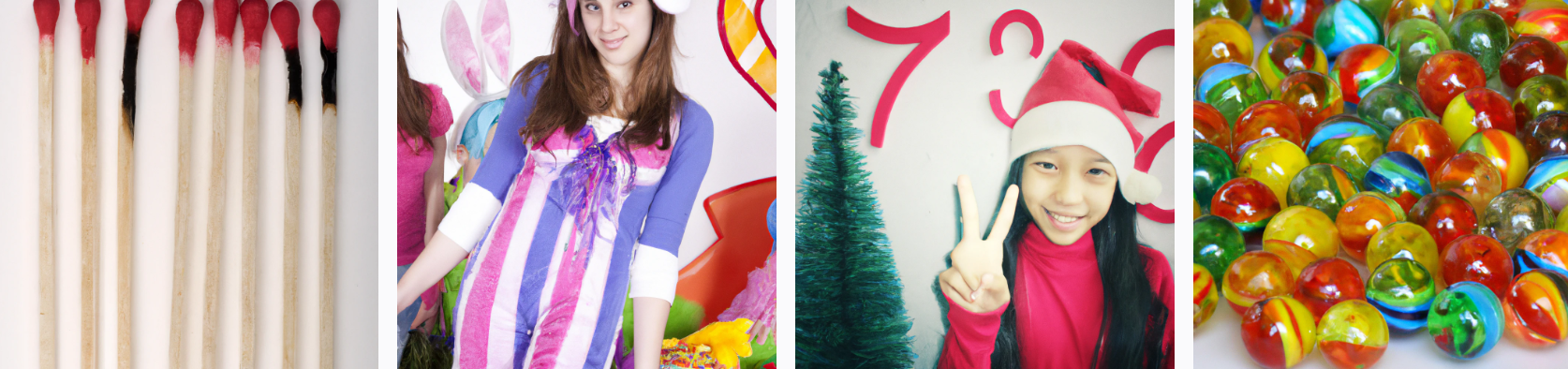
“Eight”

“Nine”

“Ten”
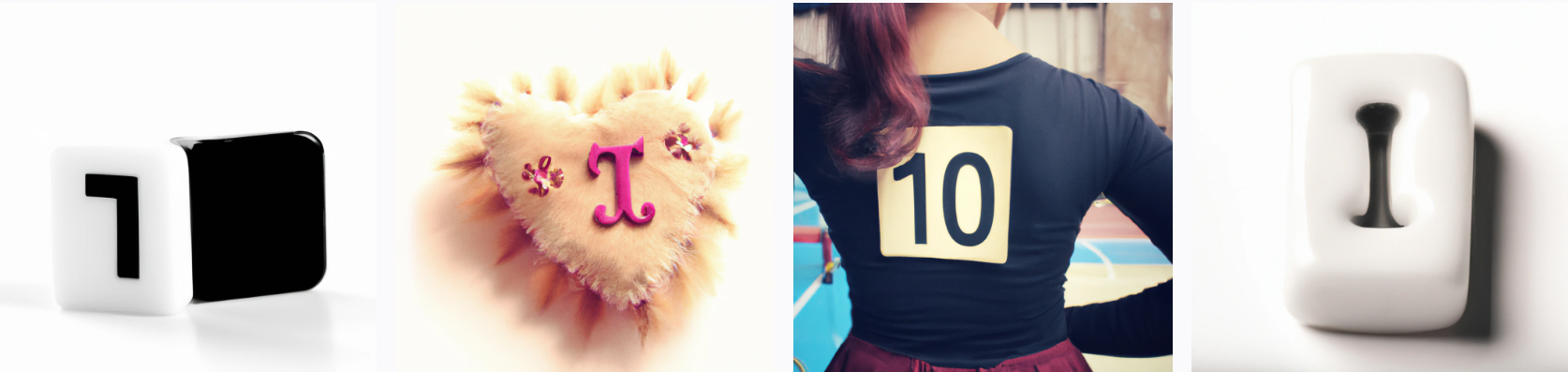
“One hundred”

Digits
“0”

“1”

“2”

“3”

“4”

“5”
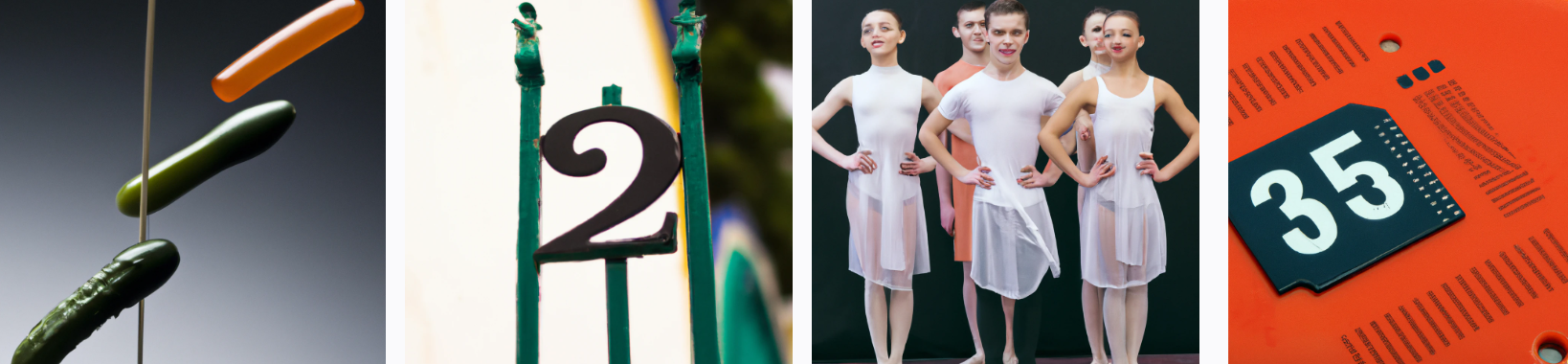
“6”

“7”

“8”

“9”

“10”

“100”

Cats
“Zero cats”

“One cat”

“Two cats”

“Three cats”

“Four cats”

“Five cats”

“Six cats”

“Seven cats”

“Eight cats”

“Nine cats”

“Ten cats”

“One hundred cats”

Reroll-eight experiment
I notice that DALL-E seems to be pretty reliable at generating 1-3 of something, and that it seems to prefer spelled-out numbers to digits. It was very successful at generating the number eight, which I suspected was due to the influence of images of magic 8-balls. It only managed to get eight cats once, maybe by accident. With my last 7 free credits, I decided to see if DALL-E had at least some sense of what it means to count to eight, as opposed to representing parts of images associated with the word “eight.”
I therefore decided to generate 7 panels of images of various objects, count the number of those objects contained in each image, plot the result, and see if it was at least centered around the number 8. The nouns were chosen with a random noun generator, and I selected the first 7 that seemed “easy to draw.” The resulting prompts were “eight paintings,” “eight hospitals,” “eight poets,” “eight historians,” “eight speakers,” “eight women,” and “eight baskets.”
The way I classified the number of objects in a given drawing is in the caption.
“Eight paintings”

“Eight hospitals”

“Eight poets”

“Eight historians”

“Eight speakers”

“Eight women”

“Eight baskets”

Results for reroll-8 experiment
Discussion on reroll-8 experiment
The reroll-eight experiment did generate 8 objects about 20% of the time.
However, I think it’s interesting that only one occurrence of 7 of an object occurred, while 9 objects were even more common than 8 objects.
This suggests to me that DALL-E has an heavy bias toward the number 9, perhaps because a 3x3 grid is a common pattern. DALL-E seems to flip over into “grid mode” or “arrangement mode” once it has decided that it needs to display more than about 5 of an object, and needs some structure for their visual composition.
Sometimes, DALL-E gets lucky and happens to choose a structure that allows it to put in 8 objects: a lineup, a semi-structured display, two rows of four, four pairs of two, a cloud, objects in a ring.
Psychologically, this makes me think about cultures in which counting is limited and imprecise (“one, two, three… many”). DALL-E hasn’t been trained to rigidly distinguish between numbers in general. It has only been trained to distinguish between numbers that are “compositionally relevant,” like the difference between 1 and 2.
Compositional reroll-8 experiment
I wanted to test this theory by seeing if DALL-E could reliably generate 8 of something if the count was specified compositionally rather than numerically. So I bought more credits.
My best idea was “An octopus holding eight [noun], one in each leg.”
I didn’t want to generate a second point of confusion for DALL-E by asking it to generate things that can’t conceivably be held in one’s hands, like hospitals. So I decided to replace the nouns with things that fit in the hands: paintings, baskets, cigarettes, newspapers, salads, coffees, and things.
“An octopus holding eight paintings, one in each leg.”

“An octopus holding eight baskets, one in each leg.”

“An octopus holding eight cigarettes, one in each leg.”

“An octopus holding eight newspapers, one in each leg.”

“An octopus holding eight salads, one in each leg.”

“An octopus holding eight coffees, one in each leg.”

“An octopus holding eight things, one in each leg.”

Discussion of compositional reroll-8 experiment
Here, we don’t see any “pull toward 9.” I’m guessing that octopus arms don’t correspond to the “grid representation.” We see a spike at 8, and then about even numbers of 4, 5, and 6 items. This could mean that DALL-E is “torn” between count and composition, or perhaps that there is a bimodal distribution of octopodal compositions in the training data—some with 4-6 items in hand, others with 8.
I tried doing a “reroll-12” experiment, replacing the numbers on a clock with 12 paintings or 12 baskets. DALL-E generates clocks textured like baskets or spattered with paint, or with baskets next to the clock, but nothing like what I was imagining.
This experiment persuades me that DALL-E can’t count. DALL-E can compose. It understands a relationship between number-containing prompts and shapes that we recognize as digits, or between number-containing prompts and arrangements of objects that correspond to those numbers. For example, prompts that contain “nine” or “9“ often have grids, frequently 3x3 grids. Prompts that contain “eight” or “8” also often contain grids, and since grids are often in a 3x3 shape, images containing 9 objects are also associated with prompts containing the word “eight.”
This pushes me somewhat toward a concept of human psychology in which our brains are composed of a large assemblage of specialized training modules for a variety of tasks. These training modules are interconnected. For example, those of us who received an education in arithmetic have it available for use in a wide variety of tasks. Learning “when to apply arithmetic” is probably also a specialized module.
This suggests to me that advanced AI will come from designing systems that can learn new, discrete tasks (addition, handling wine glasses, using tone of voice to predict what words a person will say). It will then need to be able to figure out when and how to combine then in particular contexts in order to achieve results in the world. My guess is that children do this by open-ended copying—trying to figure out some aspect of adult behavior that’s within their capabilities, and them copying it with greater fidelity, using adult feedback to guide their behavior, until they succeed and the adult signals that they’re “good enough.”
Pedagogically, this makes me suspect that even adults need to have a much greater component of blind copying when they’re trying to learn a new skill. I often have great difficulty learning new math and engineering skills until I’ve had the chance to watch somebody else work through a significant number of problems using the techniques we’ve just learned about. Even reading the descriptions in our textbooks carefully doesn’t make it “click.” That only tells me what equations to use, and what the arguments for them are. To make use of them, I have to see them being used, and sort of “think along with” the person solving them, until I’m able to predict what they’ll do, or retrace what they just did and why they did it.
Eventually, the generalized patterns underpinning their behaviors come together, and I’m able to solve novel problems.
This makes me think, then, that math and engineering students would benefit greatly from receiving large volumes of problems with step-by-step solutions. They’d “solve” these problems along with the author. Perhaps first, they’d read the author’s solution. Then they’d try to reconstruct it for themselves. Once they can solve the problem on their own, without reference to the author’s original work, they’d move on to the next problem. Eventually, they’d try solving problems on their own.
What happens when you input “The number 0/zero” etc.?
I started by replicating my experiments using “The number [digit]” from 0-10 and including 100. Interestingly, DALL-E is 100% accurate until 100, when it throws in an extra zero on one of the images.
What happens if we start doing less common two-digit numbers, like 41, 66, and 87?
DALL-E seems to like duplicating individual digits. I’d guess that this is because all numbers from 60-69 contain at least one 6, so it’s weighted heavily toward having any given digit in images containing “the number [6X]” be a 6.
What if we generate a few more non-duplicate double digits, like 23, 37, and 90?
DALL-E was about 40% accurate here, though if we include the non-duplicate rows above as well, its overall accuracy is 30% in generating double-digit numbers.
It’s interesting to me that DALL-E pretty consistently gets the right first digit in the duplicate numbers, but fails on the second digit. Does that pattern continue into three-digit numbers? Let’s try 147, 598, and 953.
Sort of. DALL-E probably sees three-digit numbers relatively rarely, and these particular three-digit numbers almost never. My guess is that its greater success with 147 is because it contains a more common number-pair (14), which is why all its guesses are composed of those two digits. In the latter two samples, it seems to be riffing on the underlying visual similarity of 9, 5, and 6.
So it seems that DALL-E can “count” if we prompt it with “the number X” as long as X is sufficiently common in its training data to “crystallize it” if you will as an entity of its own, having a distinct identity from other similar shapes. But if we feed DALL-E prompts containing uncommon numbers, it’s biased toward low digits (because those are common) and 5-6-9 (because those are visually similar).
Kind of fun to guess at the bias on where it is getting things wrong.
I think for six, the dice is connected to the number because its a d6 which is the prototypical dice. Also the dots are kind of trying to form in the shape of the digit 6. I am also wondering whether the man is because “six” and “sex” kind of rhyme (and it thinks it is a “sexy man”).
Similarly are the attractive people standing in for 9⁄10 or 10/10?
I also notice that the people groups for 4 are “Posing for a picture” ina very stereotypical way and I am wondering whether that rhyme is in play.
And ofcourse having “three trees” is one way to dissolve ambiguity between the rhymes, why not have both?
The association of 5 with handsigns is high enough that other people are making other handsigns. Or just the part hand without big signing.
I am also wondering whether for two it is in fact doing “pairs” or “couples”.
Is the left girl trying to represent “seventeen”?
I wonder whether 8 is benefitting from needing to differentiate from “lemniscate” so it doesn’t have room to be vague.
For the six/man thing my first association was six pack. Obviously the prototypical image would be topless but my guess is topless images aren’t in the training set (or Dall-E is otherwise prevented from producing them)
This conclusion is completely unwarranted. You should not be pushed at all towards anything by these results except towards what you already knew: “unCLIP makes some serious tradeoffs in trading away correctness for artistic prettiness and is already a dead-end hack no one else is using”. Remember, you are not studying ‘neural nets’ (much less ‘psychology’). You are not studying ‘image generation neural nets’, nor ‘autoregressive models’ nor ‘diffusion models’ nor ‘DALL-E 1 models’. You are not even studying ‘GLIDE’ here. You are studying ‘unCLIP+OA diversity filter’ (note the extreme sex bias in depicted humans and all the Asians). The only thing these samples teach you about is the pathologies of unCLIP, which were already noted in the paper and which have been very pointedly noted in other papers like Imagen/Parti to not exist in those models. (Talk about looking for your keys under the lamppost!)
This is the same error Ullmann is making. Yeah, all that stuff about priors and needing new architecture paradigms is great and all that, but maybe you should show this for literally anything but DALL-E 2 (ie. unCLIP), like DALL-E 2′s own GLIDE, first, before you start talking about “steps forward” or it’s just “statistical pattern matching”… Good grief.
I wasn’t sure how to interpret this part in relation to my post here. I didn’t find the “steps forward” or “statistical pattern matching” bits in either the tweets you linked, Ullmann’s paper, or in my own post. It seems like you are inferring that I’m throwing shade on DALL-E, or trying to use DALL-E’s inability to count as a “point of evidence” against the hypothesis that AGI could develop from a contemporary AI paradigm? That’s not my intention.
Instead, I am trying to figure out the limits of this particular AI system. I am also trying to use it as a sort of case study in how visual thinking might work in humans.
I appreciate your argument that we can only use an AI system like DALL-E as a reference for the human mind insofar as we think it is constructed in a fundamentally similar way. You are saying that DALL-E’s underpinnings are not like the human mind’s, and that it’s not drawing on AI architectures that mimic it, and hence that we cannot learn about the human mind from studying DALL-E.
For context, I’d been wanting to do this experiment since DALL-E was released, and posted it the same day I got my invitation to start using DALL-E. So this isn’t a deeply-considered point about AI (I’m not in CS/AI safety) - it’s a speculative piece. I appreciate the error correction you are doing.
That said, I also did want to note that your tone feels somewhat flamey/belittling here, as well as seeming to make some incorrect assumptions about my beliefs about AI and making up quotes that do not actually belong to me. I would prefer if you’d avoid these behaviors when interacting with me in the future. Thank you.
There is no reason to think that studying unCLIP pathologies tells you anything about how human visual perception work in the first place, and it is actively misleading to focus on it when you know how it works, why it fails in the way it does, that it was chosen for pragmatic reason (diversifying samples for a SaaS business) completely unrelated to human psychology, or that more powerful models have already been show to exhibit much better counting, text generation, and visual reasoning. You might as well try to learn how intelligence works from studying GCC compile errors with
-Wall -Werrorturned on. It is strange and a waste of time to describe it this way, and anyone who reads this and then readsis worse off. None of that is shown by these results. I don’t know how you get from ‘unCLIP breaks X’ to ‘human brains may be modularized’ in the first place, the other issues with trying to learn anything from unCLIP aside.
? So, these systems, like GPT-3, T5, Parti, Imagen, DALL-E’s GLIDE etc which were all trained on unsupervised learning on old non-discrete tasks—just dumps of Internet scraped data—and which successfully learn to do these things like count in their modalities much better than DALL-E 2, will need to be trained on ‘new discrete tasks’, in order to learn to do the things that they already do better than DALL-E 2?
As for your discussion about how this is evidence for one should be totally redesigning the educational system around Direct Instruction, well, I am sympathetic, but again, this doesn’t provide any evidence for that, and if it did, then it would backfire on you because by conservation of evidence, the fact that all the other systems do what DALL-E 2 don’t must then be far more evidence in the other direction that one should redesign the educational system the opposite way to mix together tasks as much as possible and de-modularize everything.
‘Steps forward’ is in Ullmann’s last tweet:
Personally, I would advise them to step sideways, to studying existing systems which don’t use unCLIP and which one might actually learn something from other than “boy, unCLIP sure does suck for the things it sucks on”. Ullmann et al in the paper discussion further go on to not mention unCLIP (merely a hilarious handwave about ‘technical minutiae’ - yeah, you know, that technical minutiae which make DALL-E 2 DALL-E 2 rather than just GLIDE), compare DALL-E 2 unfavorably to infants, talk about how all modern algorithms are fundamentally wrong because lacking a two-stream architecture comparable to humans, and sweepingly say
(Yes, I too wonder what ‘they have learned’, Ullmann et al, considering that you didn’t study what has been learned by any of the ‘other current image generation models’ and yet consistently imply that all your DALL-E 2 specific results apply equally to them when that’s been known from the start to be false.)
The phrase “Statistical pattern matching” is in the second-most liked reply and echoed by others.
No. I am saying DALL-E 2 is deliberately broken, in known ways, to get a particular tradeoff. We can potentially learn a lot about the human brain even from AI systems which were not explicitly designed to imitate it & be as biologically plausible (and it is fairly common to try to use GPT or CNNs or ViTs to directly study the human brain’s language or vision right now). We cannot learn anything from examining the performance on particular tasks of systems broken on those specific tasks. OA deliberately introduced unCLIP to sacrifice precision of text input embedding, including things like relations and numbers, to improve the vibe of samples; therefore, those are the things which are least worth studying, and most misleading, and yet what you and Ullmann insist on studying while insistent on ignoring that.
Interesting that a lot of the faces seemed pretty realistic, given how much they emphasized how faces would be mangled intentionally.
Quandary: I honestly do not understand why we all insist on talking about GPT-3 as any kind of intelligence whatsoever. It’s an associative probability database. It doesn’t “figure” anything out, nor “decide” things, nor take any “guesses”.
Opinion: we have been influenced by a generation of technologists with an overinflated sense of self-importance bent on manipulating others with their own brand of narcissistic propaganda. Enough.
Saying “associative probability database” still leaves open the interesting question of why it associates e.g. the word “four” with a picture of three young women, or the word “six” with a digit eight surrounded by film strips or whatever that is.
I’m certainly not an expert, but these errors remind me of Moiré patterns. The meaning applied to them are more a function of how we see the errors than intrinsic properties of the system producing them.
https://en.wikipedia.org/wiki/Moir%C3%A9_pattern