The correct response to uncertainty is *not* half-speed
Related to: Half-assing it with everything you’ve got; Wasted motion; Say it Loud.
Once upon a time (true story), I was on my way to a hotel in a new city. I knew the hotel was many miles down this long, branchless road. So I drove for a long while.
After a while, I began to worry I had passed the hotel.
So, instead of proceeding at 60 miles per hour the way I had been, I continued in the same direction for several more minutes at 30 miles per hour, wondering if I should keep going or turn around.
I wasn’t sure if I was a good enough writer to write a given doc myself, or if I should try to outsource it. So, I sat there kind-of-writing it while also fretting about whether the task was correct.
(Solution: Take a minute out to think through heuristics. Then, either: (1) write the post at full speed; or (2) try to outsource it; or (3) write full force for some fixed time period, and then pause and evaluate.)
I wasn’t sure (back in early 2012) that CFAR was worthwhile. So, I kind-of worked on it.
An old friend came to my door unexpectedly, and I was tempted to hang out with her, but I also thought I should finish my work. So I kind-of hung out with her while feeling bad and distracted about my work.
A friend of mine, when teaching me math, seems to mumble specifically those words that he doesn’t expect me to understand (in a sort of compromise between saying them and not saying them)...
Duncan reports that novice Parkour students are unable to safely undertake certain sorts of jumps, because they risk aborting the move mid-stream, after the actual last safe stopping point (apparently kind-of-attempting these jumps is more dangerous than either attempting, or not attempting the jumps)
It is said that start-up founders need to be irrationally certain that their startup will succeed, lest they be unable to do more than kind-of work on it...
- Speaking of Stag Hunts by (6 Nov 2021 8:20 UTC; 192 points)
- Impact obsession: Feeling like you never do enough good by (EA Forum; 23 Aug 2023 11:32 UTC; 164 points)
- Cryonics signup guide #1: Overview by (6 Jan 2021 0:25 UTC; 151 points)
- Meadow Theory by (9 Mar 2022 17:13 UTC; 136 points)
- EA & “The correct response to uncertainty is *not* half-speed” by (EA Forum; 9 Apr 2023 16:39 UTC; 83 points)
- Unofficial Canon on Applied Rationality by (15 Feb 2016 13:03 UTC; 65 points)
- “Which chains-of-thought was that faster than?” by (22 May 2024 8:21 UTC; 37 points)
- 's comment on The Parable of the King and the Random Process by (4 Mar 2023 4:26 UTC; 35 points)
- Are you allocated optimally in your own estimation? by (EA Forum; 20 Aug 2022 21:19 UTC; 28 points)
- 's comment on Don’t Over-Update On Others’ Failures by (EA Forum; 15 Feb 2023 18:53 UTC; 25 points)
- Confidence all the way up by (17 Jan 2016 2:00 UTC; 25 points)
- 's comment on Social Dark Matter by (22 Nov 2023 8:29 UTC; 24 points)
- 's comment on #3: Choosing a cryonics provider by (20 Jan 2021 17:38 UTC; 23 points)
- Confidence all the way up by (EA Forum; 17 Jan 2016 6:00 UTC; 16 points)
- What are the top 1-10 posts / sequences / articles / etc. that you’ve found most useful for yourself for becoming “less wrong”? by (27 Mar 2022 0:37 UTC; 14 points)
- 's comment on Probabilistic decision-making as an anxiety-reduction technique by (17 Jul 2018 10:44 UTC; 13 points)
- 's comment on Why I No Longer Prioritize Wild Animal Welfare by (EA Forum; 16 Feb 2023 15:04 UTC; 10 points)
- EAGT Coffee Talks: Two toy models for theoretically optimal pre-paradigmatic research by (EA Forum; 22 Aug 2022 21:33 UTC; 8 points)
- 's comment on Shutting Down the Lightcone Offices by (17 Mar 2023 18:47 UTC; 6 points)
- Are you allocated optimally in your own estimation? by (20 Aug 2022 19:46 UTC; 6 points)
- 's comment on Finding Useful Things by (19 Sep 2023 11:37 UTC; 5 points)
- EAGT Coffee Talks: Two toy models for theoretically optimal pre-paradigmatic research by (24 Aug 2022 11:49 UTC; 5 points)
- 's comment on Some advice on independent research by (EA Forum; 9 Nov 2022 14:40 UTC; 4 points)
- 's comment on Why I No Longer Prioritize Wild Animal Welfare by (EA Forum; 15 Feb 2023 19:13 UTC; 4 points)
- 's comment on On Doing the Improbable by (21 Nov 2019 19:52 UTC; 4 points)
- Weighing in solipsism by (EA Forum; 28 Apr 2023 16:57 UTC; 3 points)
- 's comment on Why defensive writing is bad for community epistemics by (EA Forum; 11 Oct 2022 6:38 UTC; 3 points)
- 's comment on Anthropic Commits To Model Weight Preservation by (6 Nov 2025 17:29 UTC; 3 points)
- 's comment on Shutting Down the Lightcone Offices by (20 Mar 2023 9:30 UTC; 3 points)
- 's comment on Research snap-shot: question about Global Workspace Theory by (16 Jun 2020 8:21 UTC; 2 points)


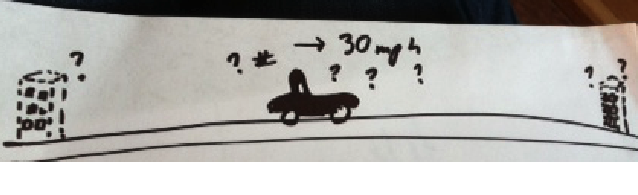
I think for me the problem is that I’m not being Bayesian. I can’t make my brain assign 50% probability in a unified way. Instead, half my brain is convinced the hotel’s definitely behind me, half is convinced it’s ahead, they fail to cooperate on the epistemic prisoner’s dilemma and instead play tug-of-war with the steering wheel. And however I decide to make up my mind, they don’t stop playing tug-of-war with the steering wheel.
My brain often defaults to thinking of these situations in terms of potential loss, and I find the CFAR technique of reframing it as potential gain helpful. For example, my initial state might be “If I go ahead at full speed and the hotel is behind me, I’ll lose half an hour. But if I turn around and the hotel is ahead of me, I’ll also lose time.” The better state is “By default, driving at half speed might get me to the hotel in 15 minutes if I’m going in the right direction, and I’ll save ~8 minutes by going faster. Even if the hotel is behind me, I’ll save time by driving ahead faster.”
Reminds me of the motto “Strong Opinions, Weakly Held”. There’s no point having a blurry opinion, or not expressing what you believe to be the most likely candidate for a good way forward, even if it’s more likely by only a small margin. By expressing (and/or acting on) a clearly expressed, falsifiable opinion, you expose it to criticism, refutation, improvement, etc. And if you hold it weakly, then you will be open to reconsidering. Refusing to make up your mind, and kindof oscilating between a few options, perhaps waiting to see where the wind blows, has its advantages, but especially when it comes to getitng things done, is most often a clear loser. Despite this, our brains seem to prefer it instinctively, maybe due to some ancestral environment echoes about being proven wrong in the eyes of the tribe?
Very good and timely observation. A study came out just a few a days ago in Nature Neuroscience showing that the brain tends to implement competing sensorimotor policies simultaneously (a sort of model averaging), at least at the beginning of a movement: Parallel specification of competing sensorimotor control policies for alternative action options. (With this link you should be able to go through the paywall.)
By the way, this form of policy averaging is not wrong per se; it is wrong with respect to a given goal (aka loss function). It’s not ideal if you want to reach the hotel (0-1 loss); it could be locally optimal (probably still not globally optimal, depending on your posterior), if you wanted to minimize the average (squared) distance from the hotel. Which is not what we usually want to do for hotels (if we are uncertain between building A and building B we are not just happy to stand in the middle), but it might be the right loss function in other cases.
I thought the heuristic was “if I think I passed the hotel, I was going too fast to notice. I better slow down so I see it when I come up on it, or so I might recognize a landmark/road that indicates I went too far.” We slow down not because we are splitting the difference between turning around and continuing on. We slow down to make it easier to gather more information, a perfectly rational response.
Yes, Thays what I think happens. I guess that stopping could be a “better” way of doing it, but if you’re unsure the hotel might be ahead, keep going while trying to gather proper orientation may not be the worse. That would require lower speeds. If the example was about a frozen lake and you were driving over what you thought was thin ice, maybe being very careful with any momentum change should apply. I guess that may be the core underlying concern in sensitive situations.
Wasn’t sure if should have stayed at a job or applied for grad school, so I quarter-assedly worked on school applications while quarter-assedly pretending to work until I got fired.
Anyone have a better procedure for fixing this than the following?
Notice the feeling.
Treat it as a signal that your S1 wants you to search for cheaper ways to figure out which option is right than continuing to drive. Search for cheaper ways and execute them. Make it a thorough search and show your S1 the thoroughness of your search. Acknowledge the awfulness of “drive back and forth in an expensive search pattern” and only choose that as a last resort.
If you don’t immediately become much more certain of which way the hotel is in, and the “go 30mph” feeling does not go away, treat it as a signal that your S1 thinks the thought process by which you chose (under evidence-starvation) is wrong, which does not necessarily mean that the conclusion is wrong.
List the ways your S1 thinks you’re biased which are screwing up your evidenced-starved reasoning.
Perform sanity-inducing rituals to counter those biases. (Think about your actual goal of getting to the hotel as soon as possible, forgive yourself for maybe driving past it, imagine all 4 outcomes (60mph forward, 60mph backward) x (get to hotel on next try after this, don’t get to hotel on next try after this) and how you would feel about them)
If the feeling is still there, this procedure has failed.
My procedure is probably similar cost, but more general:
State my goal(s), e.g. “get to the hotel”
Find the point of highest uncertainty towards the goal, e.g. “not sure if the hotel is ahead or behind me”
Come up with plans for reducing the uncertainty, e.g. “find the next gas station and ask someone”
Check whether the plan I have actually feels like it’ll work
Note that this can be applied pretty broadly, e.g. to business strategy, software design, making friends etc.
My current model is that closed/exploitation mode just can not handle ambiguity. So the generalized cue becomes: notice ambiguity->pop into open/exploration mode and figure out what heuristic I actually endorse->back to closed mode.
Open mode: generating checklists
Closed mode: executing checklists
Open and closed research summary: https://www.youtube.com/watch?v=Qby0ed4aVpo
When the implications of the situation are clearly perceived, the right action is effortless.
I agree, for a certain sense of the word “clearly”. The procedure is to make you clearly understand the implications of the situation, which can be harder for some instantiations of the situation.
My solution is rather simple: use a map.
http://lesswrong.com/lw/bwp/please_dont_fight_the_hypothetical/
Whomever downvoted this, can you explain what’s so bad about looking at a map before you go to directions unknown? Maps are simple to use AND provide useful information. There’s no reason not to use a map.
It wasn’t me, but at a guess I’d say, irrelevance to the subject of the post. Which is not about how to find a hotel.
Imagine an undirected graph where each node has a left and right neighbor (so it’s an infinitely long chain). You are on a node in this graph, and somewhere to the left or right of you is a hotel (50/50 chance to be in either direction). You don’t know how far—k steps for an arbitrarily large k that an adversary picks after learning how you will look for a hotel.
The solution that takes 1 step left, 2 steps right, 3 steps left, etc. will find the hotel in O(k^2) steps. Is it possible to do better?
I can get O(k).
Since the problem posed is scale free, so should the solution be, and if there is a solution it must succeed in O(k) steps. Increase step size geometrically instead of linearly, picking an arbitrary distance for the first leg, and the worst-case is O(k), with a ratio of 2 giving the best worst-case value approaching 9k. The adversary chooses k to be much larger than the first leg and just after one of your turning points.
In the non-adversarial case, if log(k) is uniformly distributed between the two turning points in the right direction that enclose k, the optimum ratio is still somewhere close to 2 and the constant is around 4 or 5 (I didn’t do an exact calculation).
ETA: That worst-case ratio of 9k is not right, given that definition of the adversary’s choices. If the adversary is trying to maximise the ratio of distance travelled to k, they can get an unbounded ratio by placing k very close to the starting point and in the opposite direction to the first leg. If we idealise the search path to consist of infinitely many steps in increasing geometric progression, or assume that the adversary is constrained to choose a k at least one quarter of the first step, then the value of 9k holds.
They can’t, because this is all happening in a discrete setting (“Imagine an undirected graph...”) where the minimum possible distance is 1 and your initial distance isn’t going to vary over a very large range.
Grow your steps in powers of 2 instead of linearly.
Does the solution have to be deterministic? If an adversary places the hotel after looking at my algorithm, my first inclination is introduce uncertainty into my search.
No. But you can’t do better than O(k) anyways, and you can do O(k) deterministically.
Randomising the length of the first step will improve on the constant factor by about 2. Similar analysis to the non-adversarial case, and with the same ETA I just added to my earlier comment.
If you make the run lengths increase exponentially instead of linearly then you get O(k) unconditionally.
I know. I was improving the constant factor.
Ah yes, OK, essentially the same randomization helps against an adversary when you’re growing exponentially as when you’re growing only linearly. Fair enough.
I suspect half speed is actually a rational decision given some underlying model AnnaSalamon was not aware of explicitly.
For instance, she may intuitively feel that she just passed the hotel. If so, then being extra careful to look well for features and marks around you that could give you hints of whether this happened could work best at half speed. Are there fewer hotels around? Is it a residential area? Does the amount of economic activity seems to be increasing or decreasing as I move in this direction? Then, you can turn around and get there faster.
Formalizing the precise model that would make half-speed the rational choice may be a bit complicated. But that’s what the Bayesian approach to cognitive sciences would try to do first.
The old joke about the guy searching for his spectacles under the stoplight even though he lost them elsewhere feels applicable.
In many cases people’s real drive is to reduce the internal pressure to act, not to succeed at whatever prompted that pressure. Going full speed and turning around both might provoke the shame function (I am ignoring my nagging doubts...), but doing something, anything, in response to it quiets the inner shouting, even if it is nonsensical.
Although not as clearly as the other links, Lawful Uncertainty seems quite relevant to this article.
This article only makes sense if there’s no confusion about whether a building is your hotel or not. Half-speed makes a lot of sense if you’re interested in paying close attention to what is going on around you. It’s also very useful to slow down if you become drastically uncertain, because if you don’t know where you’re going it’s better not to be going in random direction at full speed while you’re thinking about it.
I read this and all I could think of was myself and a script I have just been running away from writing. I talk more about it than I do actually writing it because the first draft got some criticism. I should just write the 2nd draft, get to know what I did wrong, what I did better and keep writing. How else would I improve if the thought remains only in my head?
For the hotel example I think slowing down initially isn’t a bad idea. It allows your mind room to think but you don’t want to stay at that speed because you do want to get to the hotel eventually. You need to in that time make a decision, forward or backward and strategy to adopt so you don’t speed up and still maybe miss seeing the hotel because you are driving fast in unfamiliar territory.
Having a strategy with which is speed N can be a good approach and also stopping to ask questions. Either way, i think the tug of war going on in the mind is a necessary tool that slows us down, gives the mind time to think before preceding
Huh. I think I’ve been doing this at my current (crappy, unlikely to lead anywhere, part-time remote contract programming) job. Timely!
Nah… in the hotel example, you slow down as to not maximize your mistake if you’ve made one. If you have doubts, they are probably justified enough to do something to examine the evidence while minimizing the fallout.
Before you set out on the trip, you’d likely have checked some map and had an idea of how far to travel along the road the hotel is located on. You’d say, “Oh. It’s 17.8 miles after I turn onto highway 99. Got it.”
Then, you turn onto highway 99, but you’d be thinking about something other than “17.8 miles to go”. You’d be thinking about the big meeting you had the next day, or the cramp in your leg, or your ex-girlfriend, etc. So x miles would pass, and you’d lose track of what the value of x was.
At this point, you’re right that driving full speed either forward or back would optimize your arrival time IF you guess right. But during the time you are trying to make a decision, it makes rational sense to slow your speed a bit and think. (30 mph seems excessive in a 60mph zone)
You probably didn’t pass the hotel yet. I’d say it’s north of 50% probability. While you were daydreaming about the big meeting and your ex, you weren’t completely distracted from the task of finding your hotel—you were just daydreaming, not actually dreaming. Add this to the fact you’d have some reasonable idea of how many miles you’d traveled since turning onto hwy 99, and it’s a 50.1%+ chance you didn’t miss your hotel yet.
Slowing down for a minute is certainly preferable to just turning around the moment you have a doubt. It’s also better than just proceeding through your doubts at the same speed and making the problem worse.
Slowing down gives you a chance to look around and check for clues that you may have missed, or not yet arrived at the hotel. It allows you to think and reason through the evidence. Did you already pass a commercial district and now you are in the rural boonies? Or have you not yet seen an area where a hotel might be?
The other examples don’t seem to fit the first analogy that well. If the point is “it’s rational to commit to one thing since half-assing two things tends not to work” then I agree, but it’s not terribly novel stuff. (65 upvotes? Really?)
I’ve been making this mistake for the past few years of my life
#feelsbadman
If you believe that you will have evidence in the future that enables you to decide between in front of you and in back of you, driving slowly may be the optimal decision. For instance, assume you think that the hotel can be in one of two locations, either a specific spot ahead of you or a specific spot behind you, and you are not equidistant from those two locations, you will receive evidence a fixed time in the future, and if you travel at half speed you will receive the evidence when you are equidistant between the two possible locations. Then travelling at any speed (that doesn’t pass the hotels) will not change the average distance to the hotel at the moment you find the evidence, but travelling at a speed designed to put you in the middle when you get the evidence will reduce the worst case scenario without affecting the average. Therefore you should travel at half speed. Furthermore, it may reduce the average as well if the chance of receiving evidence varies on how much total distance you have travelled (seeing a landmark that you know is past or before the hotel would be evidence, for instance).
Of course I’ve defined this scenario in a bunch of arbitrary ways, but they aren’t really necessary to make the optimal result travelling at half speed, they just make the optimality easier to demonstrate.
When there’s no clear winner, the winner can’t take all.
https://en.wikipedia.org/wiki/Winner-take-all_in_action_selection
Happens all the time in decision theory & reinforcement learning: the average of many good plans is often a bad plan, and a bad plan followed to the end is often both more rewarding & informative than switching at every timestep between many good plans. Any kind of multi-modality or need for extended plans (eg due to upfront costs/investments) will do it, and exploration is quite difficult—just taking the argmax or adding some randomness to action choices is not nearly enough, you need “deep exploration” (as Osband likes to call it) to follow a specific hypothesis to its limit. This is why you have things like ‘posterior sampling’ (generalization of Thompson sampling), where you randomly pick from your posterior of worlds and then follow the optimal strategy assuming that particular world. (I cover this a bit in two of my recent essays, on startups & socks.)
Good post.
Though as is often the case, there is already a well-known saying that encapsulates this idea: “do it properly or not at all”.
There’s an important category of choices: the ones where any good choice is “acting as if” something is true.
That is, there are two possible worlds. And there’s one choice best if you knew you were in world 1, and another choice best if you knew you were in world 2. And, in addition, under any probabilistic mixture of the two worlds, one of those two choices is still optimal.
The hotel example falls into this category. So, one of the important reasons to recognize this category is to avoid a half-speed response to uncertainty.
Many choices don’t fall into this category. You can tell because in many decision-making problems, gathering more information is a good decision. But, this is never acting as if you knew one of the possibilities for certain.
Arguably in your example, information-seeking actually was the best solution: pull over and take out a map or use a GPS.
It seems like another important category of choices is those where the best option is trying the world 1 choice for a specified amount of time and then trying the world 2 choice. Perhaps these are the choices where the best source of information is observing whether something works? Reminds me of two-armed bandit problems, where acting-as-if and investigating manifest in the same kind of choice (pulling a lever).
As a general response to uncertainty, half-speed can have advantages. Specifically:
This signals your uncertainty to others—someone more familiar with the area may offer to help.
When (and if) help is offered, you are less likely to have gone too far the wrong way.
Now, neither of these were applicable in your specific hotel case—had there been anyone to ask, you could have stopped and asked, and going slowly in a car doesn’t really help you. So it makes a lot of sense to ignore the default strategy in that case—and, in fact, in several other cases as well (it’s a common heuristic, but it really doesn’t apply in a lot of situations)
Averages don’t work that way because you did the math wrong: you should have stopped! I understand the point that you’re trying to make with this post, but there are many cases in which uncertainty really does mean you should stop and think, or hedge your bets, rather than go full speed ahead. It’s true there are situations in which this isn’t the case, but I think they’re rare enough that it’s worth acknowledging the value of hesitation in many cases and trying to be clear about distinguishing valid from invalid hesitation.
It seems to me that thinking through uncertainties and scenarios is often really really important, as is making specific safeguards that will help you if your model turns out to be wrong; but I claim that there is a different meaning of “hesitation” that is like “keeping most of my psyche in a state of roadblock while I kind-of hang out with my friend while also feeling anxious about my paper”, or something, that is very different from actually concretely picturing the two scenarios, and figuring out how to create an outcome I’d like given both possibilities. I’m not expressing it well, but does the distinction I am trying to gesture at make sense?
Yup.
If you take a weighted sum of (75% likely 60mph forward) + (25% likely 60 mph backward), you get (30 mph forward).
Stopping briefly to choose a plan might’ve been sensible, if it was easier to think while holding still; stopping after that (I had no GPS or navigation ability) wouldn’t’ve helped; I had to proceed in some direction to find out where the hotel was, and there was no point in doing that not at full speed.
Often a person should hedge bets in some fashion, or should take some action under uncertainty that is different from the action one would take if one were certain of model 1 or of model 2. The point is that “hedging” or “acting under uncertainty” in this way is different in many particulars from the sort of “kind of working” that people often end up accidentally doing, from a naiver sort of average. Often it e.g. involves running info-gathering tests at full speed, one after another. Or e.g., betting “blue” each time in this experiment, while also attempting to form better models.
I suppose this is a good example of such roads. My general impression is that people are nitpicky because it would be rather difficult to miss a hotel, especially on a long, visual-infinity, featureless roads like that.