Problem Solving with Mazes and Crayon
I want to talk about a few different approaches to general problem solving (for humans). It turns out that they can all be applied to mazes, so I’ll use some disney-themed mazes to illustrate each approach.
We’ll start off with some traditional path-search algorithms (DFS, BFS, heuristic). Next, we’ll talk about how these algorithms can fall short for everyday problem solving. Then we’ll move on to the interesting part: two techniques which often work better for everyday problem solving, and lend some interesting insights when applied to mazes.
I’ll assume no technical background at all, so if you’ve seen some of this stuff before, feel free to skim it.
DFS and BFS
You have a maze, with a start point and an end point, and you are searching for a path through it. In algorithms classes, this problem is called “path search”.

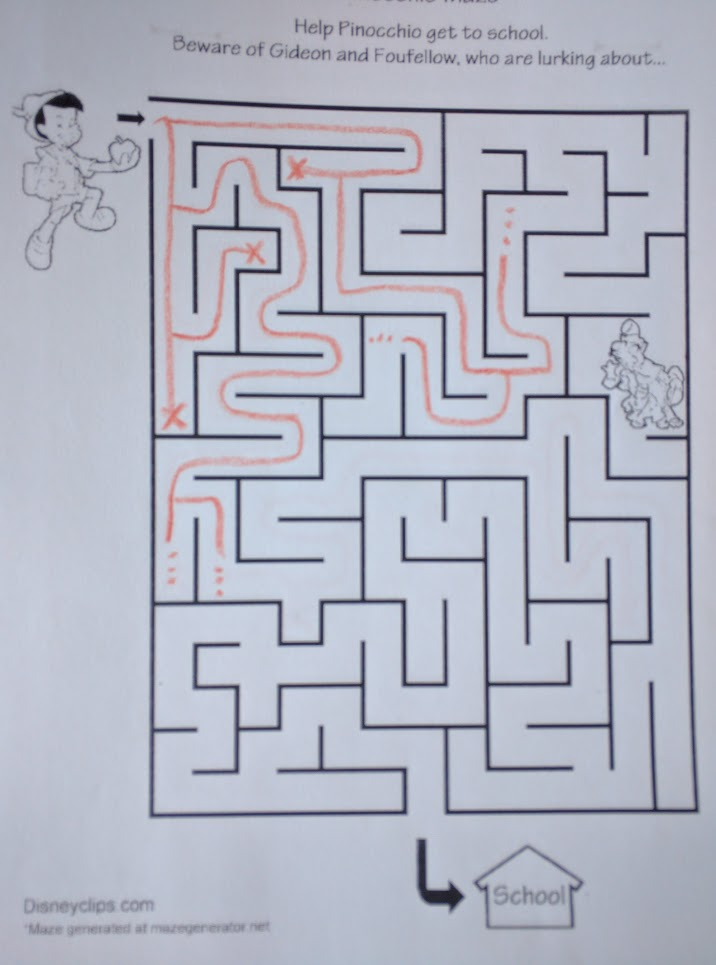
The very first path search algorithms students typically learn are depth-first search (DFS) and breadth-first search (BFS). Here’s DFS, applied to the Pinocchio maze above:
Basically, the DFS rule is “always take the right-most path which you haven’t already explored”. So, in the Pinoccchio maze, we start out by turning right and running until we hit a wall (the first “x”). Then we turn around and go back, find another right turn, and hit another dead end. Turn around again, continue…
That’s depth-first search. We go as far as we can down one path (“depth-first”) and if we hit a dead end, we turn around, back up, and try another path.
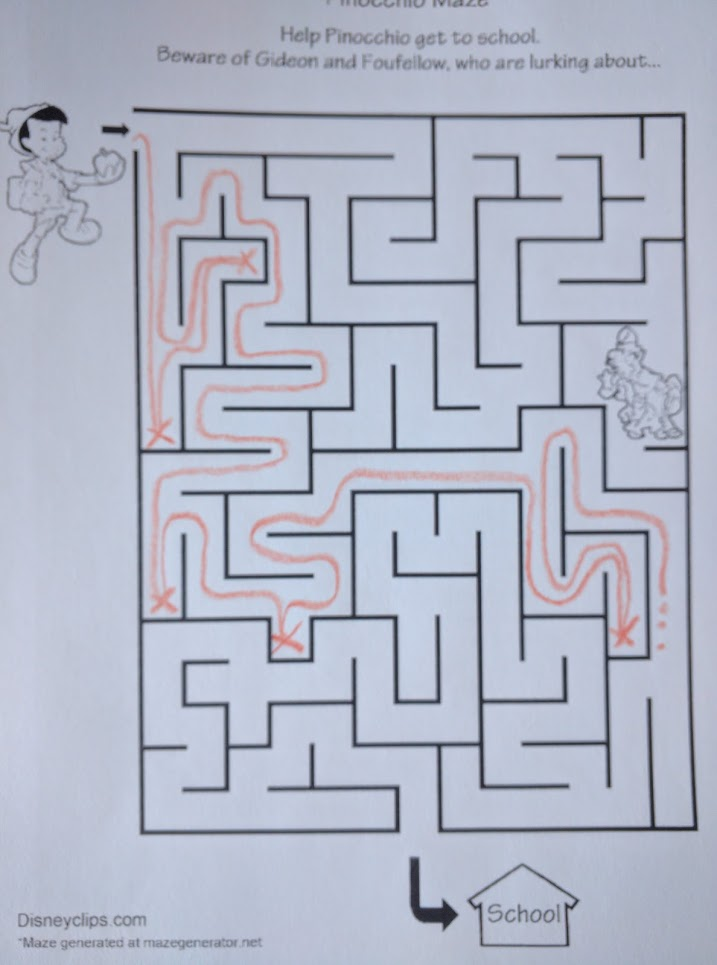
Breadth-first search, on the other hand, tries all paths in parallel:
In this snapshot, we’ve hit three dead ends, and we have four separate “branches” still exploring the maze. It’s like a plant: every time BFS hits an intersection, it splits and goes both ways. It’s “breadth-first”: it explores all paths at once, keeping the search as wide as possible.
There’s lots more to say about these two algorithms, but main point is what they have in common: these are brute-force methods. They don’t really do anything clever, they just crawl through the whole maze until they stumble on a solution. Just trying out paths at random will usually solve a maze about as quickly as DFS or BFS (as long as you keep track of what you’ve already tried).
Let’s be smarter.
Heuristic Search
A human solving a maze usually tries to work their way closer to the end. If we’re not sure which way to go, we take the direction which points more toward the goal.
Formalizing this approach leads to heuristic search algorithms. The best-known of these is A*, but we’ll use the more-human-intuitive “greedy best-first” search. Like breadth-first search, best-first explores multiple paths in parallel. But rather than brute-force searching all the paths, best-first focuses on paths which are closest to the goal “as the bird flies”. Distance from the goal serves as an heuristic to steer the search.
Here’s an example where best-first works very well:
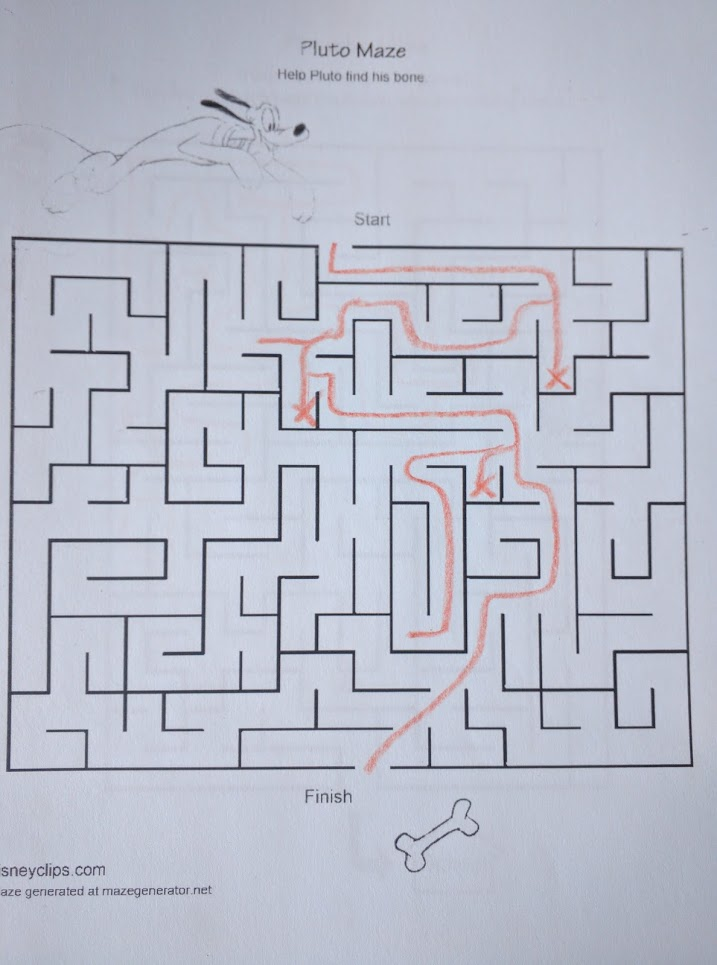
By aggressively exploring the path closest to the goal, Pluto reaches his bone without having to explore most of the maze.
But heuristic search comes with a catch: it’s only as good as the heuristic. If we use straight-line distance from the goal as an heuristic, then heuristic search is going to work well if-and-only-if the solution path is relatively straight. If the solution path wiggles around a lot, especially on a large scale, then heuristic search won’t help much. That’s what happens if we apply best-first to the Pinocchio maze:
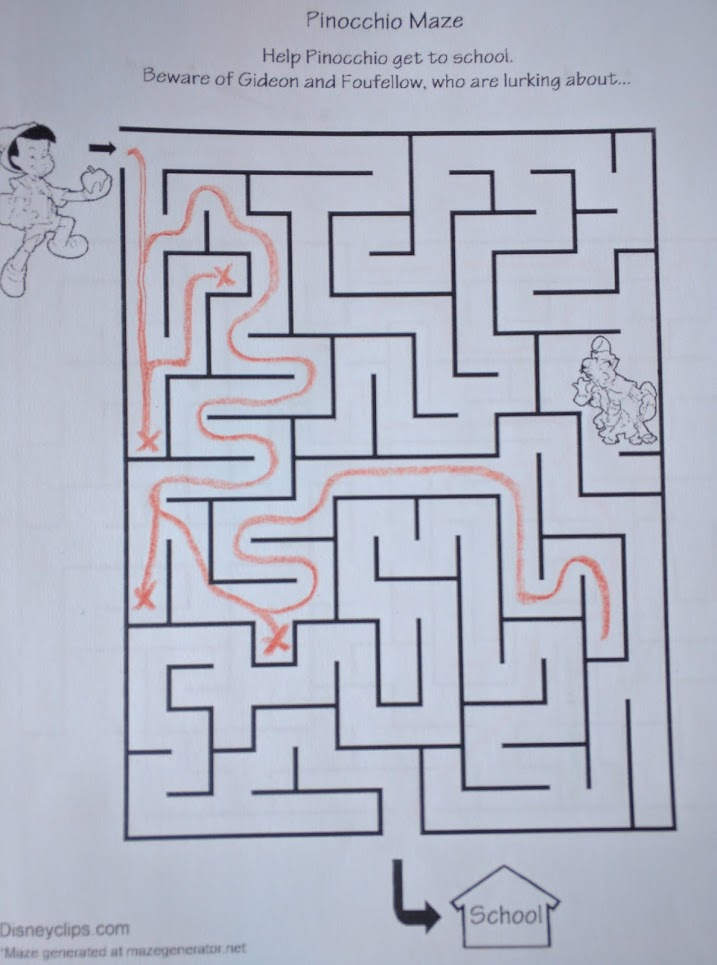
… the best-first solution in this case is almost identical to DFS.
General Problem Solving
In AI, path search is used to think about solving problems in general. It turns out all sorts of things can be cast as path search problems: puzzles, planning, and of course navigation. Basically any problem whose solution is a sequence of steps (or can be made a sequence of steps).
What do our maze-solving algorithms look like in a more general problem-solving context?
Brute-force search is, well, brute-force search. It’s trying every possible solution until you hit on one which works. If we use the random variant, it’s randomly trying things out until you hit something which works. I do not recommend solving problems this way unless they are very small, very simple problems.
Heuristic search is more like how most people solve problems, at least in areas we aren’t familiar with. We’ll have some heuristics, and we’ll try stuff which the heuristics suggest will work well.
One common version of heuristic search in real-world problem solving is babble and prune: brainstorm lots of random ideas, then pick out a few which seem promising based on heuristics. Lather, rinse, repeat. This goes by many names; in design, for example, it’s called “flare and focus”. It’s like e-coli path search: flail around, run in a random direction, and if it looks like it’s working, keep going. Otherwise, flail around some more and run in a new direction.
The problem with any heuristic search is that it’s only as good as our heuristic. In particular, most heuristics are “local”: like the straight-line distance heuristic, they’re bad at accounting for large-scale problem structure. Without some knowledge of large-scale problem structure, local heuristics will lead us down many dead ends. Eventually, when we find the “right” solution, we realize in hindsight that we weren’t really solving the right problem, in some intuitive sense — more on that later.
Upping our Game
So we have algorithms which correspond to blindly flailing about (brute force), and we have algorithms which roughly correspond to how humans solve many problems (heuristics). But the real goal is to come with better ways for us humans to solve problems. We need to up our game.
For single-shot problem solving, it’s tough to do better than heuristic path search. One way or another, you have to explore the problem space.
But in the real world, we more often face multiple problems in the same environment. We have jobs, and our jobs are specialized. It’s like needing to find paths between many different pairs of points, but all in the same maze. In this context, we may be able to invest some effort up-front in better understanding the problem space (e.g. the maze) in order to more easily solve problems later on.
(Technical note: here, the usual textbook pathfinding algorithms are not so good. All-pairs path search tries to explicitly represent distances between each pair of points, which is out of the question for real-world high-dimensional problem solving.)
Bottlenecks
Here’s an interesting way to look at the Pinocchio maze:
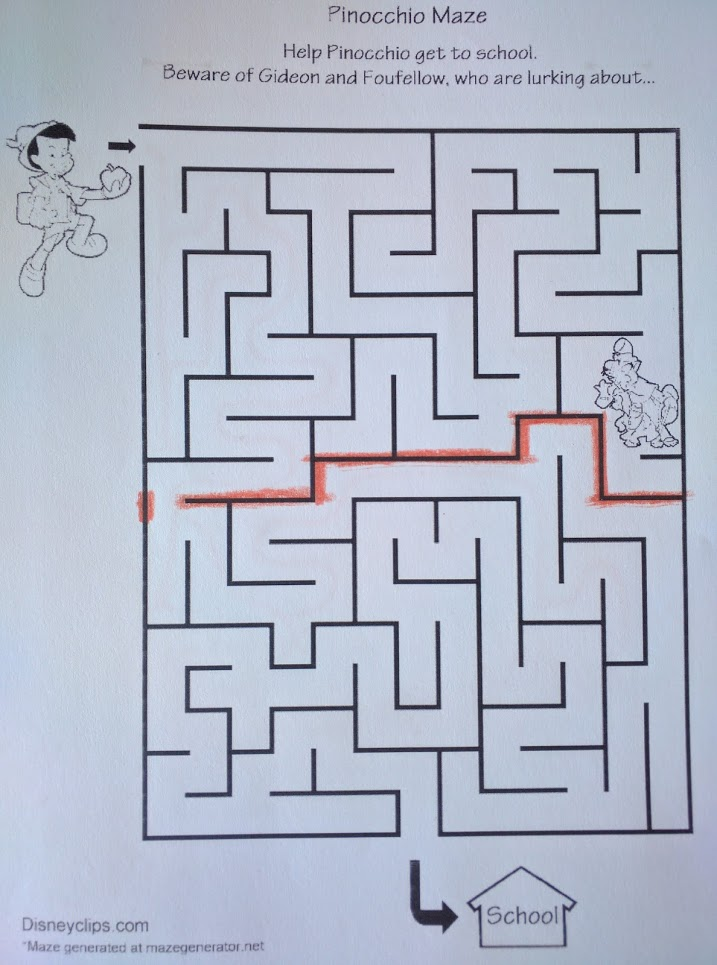
Note that the highlighted walls have exactly one gap in them. If Pinocchio wants to get from one side of the highlighted walls to the other, then he has to go through that gap.
This observation lets us break the original problem up into two parts. First, Pinocchio needs to get from the start to the gap. Next, he has to get from the gap to the end. During the first half, he can completely ignore all of the maze below the highlight; during the second half, he can completely ignore all of the maze above the highlight.
This is a bottleneck: it’s a subproblem which must be solved in order to solve the main problem.
Once we have identified a bottleneck, we can use it in conjunction with other search algorithms. For instance, rather than running heuristic search on the full maze, we can use heuristic search to get Pinocchio to the gap in the wall, and then run a second heuristic search from the gap to the end. This will do at least as well as the original heuristic search, and usually better.
Even more powerful: unlike search methods, a bottleneck can be re-used for other problems. It’s a property of the problem space, not the problem itself. If Pinocchio is starting anywhere in the top half of the maze, and needs to get anywhere in the bottom half, then the same bottleneck applies. It can even be useful to know about the bottleneck when we don’t need to solve it for the problem at hand; consider this maze:
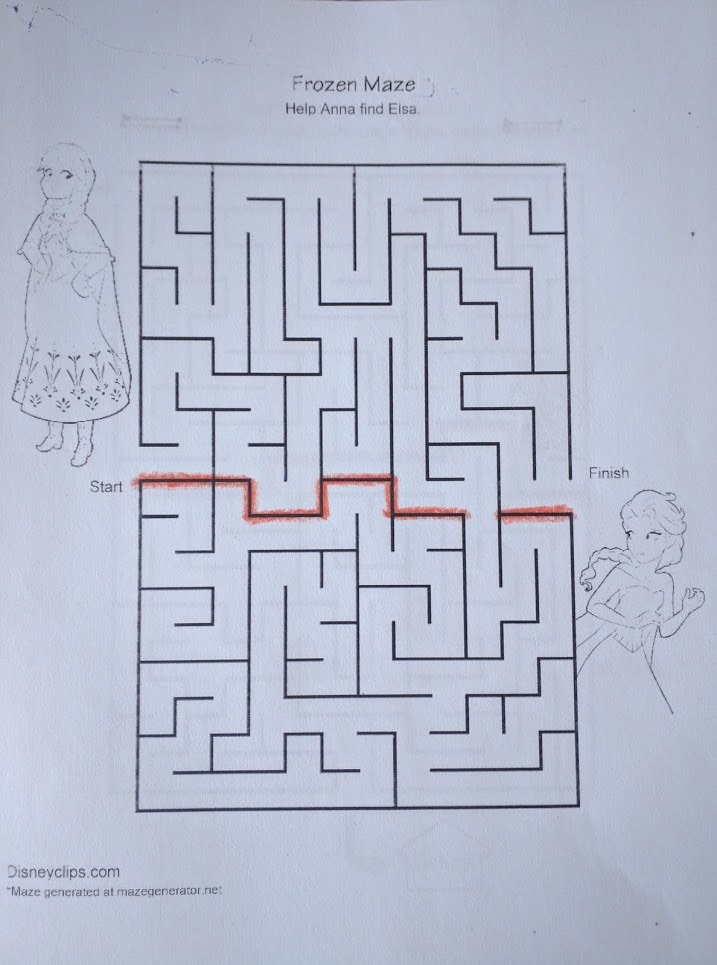
Having identified the bottleneck, we can see at a glance that the entire bottom half of the maze is irrelevant. If Anna crosses the gap, sooner or later she’ll have to turn around and come back out again in order to reach Elsa. In other words: knowing about a bottleneck you don’t need to solve is useful, because you can avoid it.
Bottlenecks in Real-World Problems
Note that, in order for the bottleneck to add value on top of heuristic search, the bottleneck should be something which the heuristic search would not efficiently solve on its own. For instance, if we’re using a straight-line-distance heuristic in a maze, then a bottleneck is most useful to know about if it’s notnear the straight line between start and finish. If there’s a bottleneck we must cross which is way out to the side, then that’s a useful bottleneck to know about.
Another way to word this: the ideal bottleneck is not just a subproblem which must be solved. It’s a maximally difficult subproblem, where difficulty is based on the original heuristics.
This is how we usually recognize bottlenecks in real-world problems. If I’m a programmer trying to speed up some code, then I time each part of the program and then focus on the section which takes longest: the slowest part is the “most difficult” subproblem, the limiting factor for performance. If I want to improve the throughput of a factory, then I look for whichever step currently has the lowest throughput. If I’m designing a tool or a product, then I start by thinking about the most difficult problem which that product needs to solve: once that’s figured out, the rest is easier.
Personally, I find a lot of “shower insights” come this way. I’m thinking about some problem, mulling over the hardest part. I focus in on the hard part, the bottleneck itself, forget about the broader context… and suddenly realize that there’s a really nice solution to the bottleneck in isolation. What’s hard with the original heuristic often becomes easy when we focus on the bottleneck itself, and apply bottleneck-specific heuristics.
In a maze, a bottleneck way to the side is hard using the straight-line distance to the finish as an heuristic. But if we aim for the gap in the wall from the start, then it’s easier.
To find the “right” solution, focus on the right problem. That’s what bottlenecks are all about.
Chunking
Let’s go back to the Anna and Elsa maze. Here’s an equivalent way to represent the bottleneck we highlighted in that maze:
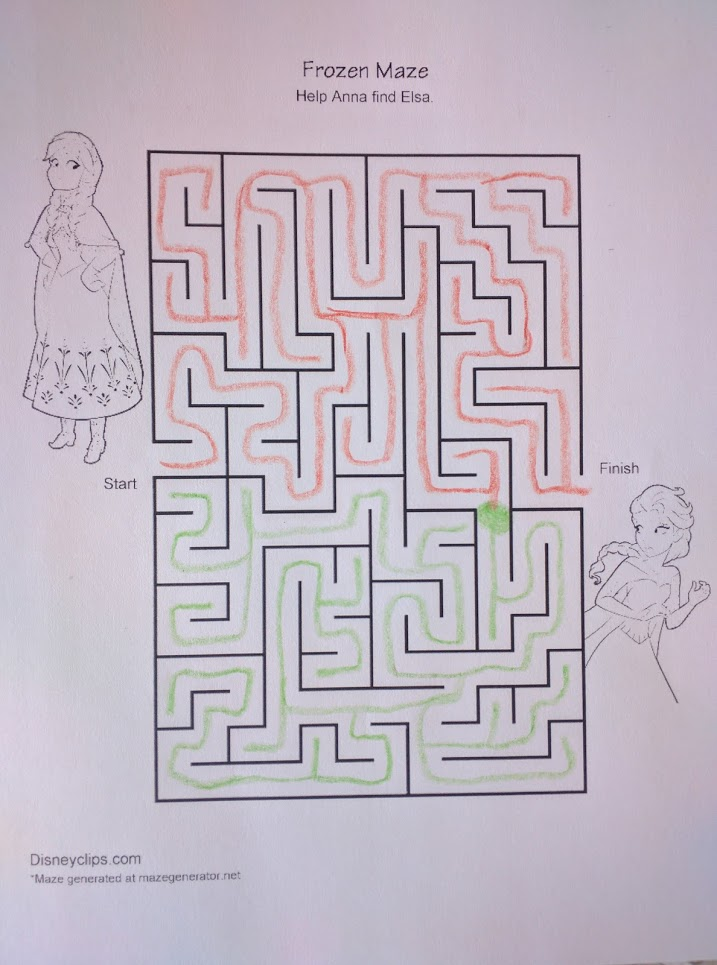
Half the maze is orange, the other half is green, and the two touch at exactly one point: the green dot, right where we identified a bottleneck. If we want to go from an orange point to another orange point, then we only need to worry about the orange part of the maze. If we want to move between orange and green, then we must cross the green point.
Here, we’ve “chunked” the maze into two pieces, and we can think about those two pieces more-or-less independently. Here’s chunking on the Pinocchio maze, with a few more colors:
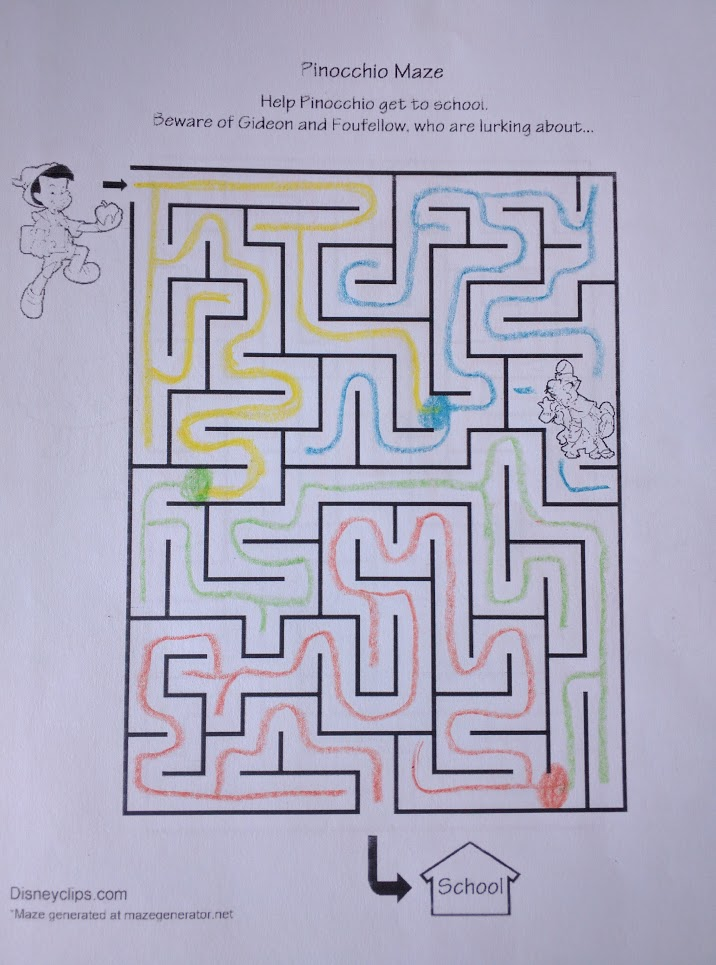
For Pinocchio to get to school, he must start in the yellow chunk and get to the orange chunk. We can only get from yellow to orange via green, so the color path must be yellow → green → orange (and we can ignore the blue part of the maze entirely). The original maze is broken into three parts, one within each color chunk, and each problem can be solved separately.
(Side question: there’s at least one more-human-intuitive way to apply chunking to mazes. Can you figure it out?)
Once we’ve represented the maze using colored chunks, and once we know how to use that information, we can use it to move between any two points in the maze. “Local” moves, within the same color chunk, can ignore all the other chunks. Larger-scale travel can focus first on the sequence of color moves — essentially a path through a larger-scale, more abstracted maze — and then zoom in to find paths within each chunk. Ideally, we choose the chunks so that an heuristic works well within each piece.
This is actually how humans think about moving around in space. Our mental map of the world contains five or six different levels, each one more granular than the last. When planning a path, we start with the highest-abstraction-level map, and then zoom in.
More generally, experts in a field process information more efficiently by chunking things together into more abstract pieces. Expert chess players don’t think in terms of individual pieces; they think in terms of whole patterns and how they interact. For a human, this is basically what it means to understand something.
Conclusion
I frequently see people tackle problems with tools which resemble heuristic path search — e.g., a brainstorming session, followed by picking out the most promising-sounding ideas.
I think a lot of people just don’t realize that there are other ways to tackle a problem. It’s possible to look at properties of the problem space — like bottlenecks or chunks — before proposing solutions. These are (some of) the pieces from which understanding is built, and when they work, they allow much more efficient and elegant approaches to problems.
- Gears-Level Models are Capital Investments by (22 Nov 2019 22:41 UTC; 181 points)
- What’s General-Purpose Search, And Why Might We Expect To See It In Trained ML Systems? by (15 Aug 2022 22:48 UTC; 158 points)
- How (not) to choose a research project by (9 Aug 2022 0:26 UTC; 79 points)
- What’s your big idea? by (18 Oct 2019 15:47 UTC; 30 points)
- 's comment on Benito’s Shortform Feed by (2 Dec 2019 0:06 UTC; 20 points)
- How well does your research adress the theory-practice gap? by (8 Nov 2023 11:27 UTC; 20 points)
- 's comment on What’s Your Cognitive Algorithm? by (18 Jun 2020 23:27 UTC; 19 points)
- 's comment on Babble by (21 Nov 2019 18:42 UTC; 14 points)
- San Francisco Meetup: Articles by (22 Jul 2018 4:32 UTC; 12 points)
- 's comment on Novelty Generation—The Art of Good Ideas by (20 Aug 2022 4:43 UTC; 3 points)
Promoted to curated, here are my thoughts:
Pro:
This post was really easy to get into, was fluently written and generally was engaging to read.
It actually taught me a potential new mental motion, or at least heavily clarified one, in the way it illustrated how bottlenecks in mazes influence the optimal strategy. I’ve done an undergraduate in CS, and so done lots of path-searching problems, and was familiar with the basic concept, but this connected my abstract idea of identifying bottlenecks with my intuitive planning sense.
Great use of pictures and visual media. I have a guess that we are lacking that on LessWrong, and that a lot of our posts could be made a lot better with more diagrams. And for that I also liked how the diagrams were kinda janky photos of pieces of papers with crayon on them, because it set an example of how you can add diagrams to a post without needing to put in a ton of time and effort in illustrator or something.
Cons:
I think I would have loved a bit more generalization of the concept of mazes. There is the difficult question of what problems are actually shaped like the maze problem analyzed in this post, and I think the biggest thing preventing me from using the ideas in this post, is a lot of uncertainty about when it is actually a good idea to apply them.
This is good as a stand-alone post, and I think it’s valuable to have stand-alone posts, but I am also always in favor of linking to existing discussion of a concept, that we’ve had on LessWrong. In this case links to the section of the sequences were Eliezer talks about a bunch of graph-search algorithms, and some of the existing writing on chunking would have been great, but I understand that finding those posts can be quite a bit of a pain.
Overall, very happy about this post.
This is great. Just one nitpick
It won’t literally do “at least as well as the original heuristic”, I’m pretty sure. You could construct a maze where going in the direction of the bottleneck leads you into a longer path than going into the direction of the end. It’ll of course do better in expectation.
Yeah, on reflection that’s right, I didn’t think it through properly.
I like the post. People naturally stick with one of the first few solutions that make sense to them (us), without investing a little more time into investigating the general properties of the problem space. We software designers are very prone to this. A couple more general patterns: working with the duals, working backwards.
Could you give a few examples of what you mean by working with the duals, both in the maze context and otherwise? It brings at least one good maze strategy to mind for me, but the word is used in multiple ways, so I’m curious whether we’re thinking of similar things.
Do you perchance know anything about higher-dimensional mazes or labyrinths? As actual games, rather than metaphors for higher-dimensional problem solving.
I do not, but I have always suspected there must be a community of such people somewhere.
No idea. Just off the top of my head, the exponential growth in volume would be an issue for mazes in higher dimensions. Four would probably still be workable, though.
There’s this http://miegakure.com/ in development for several years now
A neat example of the failings of heuristics when applied to mazes is the hedge maze at Egeskov Castle, Denmark (aerial photo, 2D diagram). It’s constructed such that if you choose paths seemingly pointing towards the goal, you’ll get caught in an infinite loop—and in fact, the most effective route can be found through a heuristic of choosing the path seemingly pointing away from the goal.
This is really interesting and easy to understand, except I feel like I’m still missing a sense of how to actually apply this to the real world. I think this would really benefit from some examples of how one might apply each strategy to specific real-world problems.
This reply is several years late, but what’s a specific real-world problem (tho maybe one closer to a ‘toy’ problem like the mazes in this post) that you think would serve as a good example for which to (try to) apply the strategies described in the post?
I won’t give any spoilers, but I recommend “how to efficiently reach orbit without using a rocket” as a fun exercise. More generally, the goal is to reach orbit in a way which does not have exponentially-large requirements in terms of materials/resources/etc. (Rockets have exponential fuel requirements; see the rocket equation.)
Does “reach orbit” mean put something in orbit or put a human being (and not kill them)? The latter seems pretty hard to do, practically, with current technology, without using rockets (to at least setup an ‘efficient’ system initially).
(Would you link to some spoilers? I’m curious what you have in mind as solutions!)
Live human being is indeed the harder version. I recommend the easier version first, harder version after.
Ah, but what specific bottlenecks make it hard? What are the barriers, and what chunking of the problem do they suggest?
Also: it’s totally fine to assume that you can use rockets for setup, and then go back and remove that assumption later if the rocket-based initial setup is itself the main bottleneck to implementation.
This is totally cruel nerd sniping by-the-way :)
;)
Excellent post! Your explanations were interesting and intuitive for me, even though I don’t know much of anything about computer science.
Thanks! Glad it made sense, I wasn’t sure it would.
I really like the maze analogy! The pictures help a whole bunch in explaining the concepts!
Related: I don’t know if this has a direct analog to a CS algorithm, but one other heuristic which seemed like it might have been good to try was drawing a line from both start and finish incrementally to see how they could touch in the middle.
Also not sure if it’s a standard concept in path search, but searching from both ends seems fruitful, even in its most naive implementations:
if the graph is sufficiently random, I think it should take the expected fraction of the maze you have to walk from N/2 to sqrt(N)
you can apply it to either BFS or DFS, though I suspect that in practice DFS works better (and even better still if you DFS by switching your first decision (rather than the OP’s algorithm of switching your last)
naturally, there’s plenty of room for layering heuristics on top, like seeking towards the opposing cursor, or even the nearest point of the opposing explored-so-far surface...
What comes to my mind is a kind of algorithm for auto-chunking: repeatedly take a dead end and fill it in until the point where it branches off from a hallway or intersection. Eventually you’re left with a single hallway from entrance to exit.
I’m not certain how it’s an improvement over DFS, though.
Answering my own musing: it’s implementable as a 2-state cellular automaton, rather than requiring the ~5 states that distributed DFS does. So there’s that.
I’m sold on the ideas of heuristics and identifying bottlenecks in solving problems. The concepts are very generally applicable. But I’m not convinced the particular mental motions for solving mazes are the correct ones for solving problems in general.
When I’m solving a math exercise like “Show that the complement of a finite set of k points in R^n is simply-connected if n ≥ 3”, I do things like
contemplate the nature of the complement of a finite set of k points in R^n until I can visualize it and correctly answer basic questions about it, like “is it finite or infinite” and “why isn’t it simply-connected if n<3″
list all the theorems in the relevant chapter of the topology book, especially the ones that tell why sets are simply-connected (probably I need to use the van Kampen theorem, but there could be others)
think about properties of the set in question that might lead me closer to the hypotheses
repeat steps 2-3 until I develop a general plan that seems likely to work (“Show that the set is homeomorphic to a different set S; partition S into sets that satisfy the hypotheses of the van Kampen theorem; use the van Kampen theorem to show that S is simply-connected; conclude that the original set is simply-connected”)
implement the plan
There are definitely heuristics here! But in topology exercises, identifying a bottleneck as severe as a one-empty-space wall is pretty rare, and chunking is usually not possible before the problem is already almost-solved. The core steps in the solution seem to be deconfusion, forward-chaining, and back-chaining, with chunking as an incidental step and identifying a bottleneck as something to happen if you’re really lucky.
When I’m answering an open-ended question like “how do I solve alignment”, I notice the same thing, with two complications:
There is often no single obvious path, either forwards or backwards. This means we need more deconfusion and better heuristics.
I also need to do much more conscious backchaining than conscious forward-chaining, so there’s also an asymmetry between the forward and reverse searches.
But it still seems to be true that bottlenecks are hard to find deliberately. I’m guessing that the examples of bottlenecks—“programmer trying to speed up some code”, or “throughput of a factory”, have a special structure that makes bottlenecks easy to find. They are already factored into serial steps, and it’s possible to find the bottleneck just by thinking about each of the steps separately.
It sounds like your current strategies are mostly adapted to the sorts of problems found in textbooks or homework assignments—problems which are “easy” in some sense. Such problems are typically already expressed in an ontology which reduces the search-space to something reasonably small, so just listing everything, forward-chaining, and back-chaining will probably be enough. In a large search space in which solutions are rare, those methods do not have the big-O efficiency to work.
That said, many of those methods are still necessary steps even on questions with larger search spaces—for instance, visualizing the main objects in the problem.
I really like this post, it’s very informative about the kind of search algorithms that exist. I had one question though, in my experience as a child solving mazes with a crayon I stumbled upon the tactic of starting at the end and getting to the beginning. This worked really well for me, but it always confused me as to why it was easier. Does anyone have a hypothesis as to why this might be?
The mazes may have been constructed to be hard from the front. (Lesser hypotheses: If you switch to the back when you notice it’s hard from the front, on average it’s going to become easier. If you switch after having explored the maze a little from the front, you already know where to go.)
Also: Searching from the back in addition to searching from the front can be really helpful in reconstructing the overall path!
In computer science, we might call this “breadth-first search from both sides” or “bidirectional search” (image); the insight being that you keep searching until your two search trees have some point in common. This is nice because you explore fewer total paths—in a large maze, the number of paths you explore grows exponentially as you get farther away from the starting location.
The analog in general problem solving might be to look both backwards and forwards. If I want to e.g. be happily married with kids in 5 years, I should not only think about my possible actions today (“go on more dates”, “reconnect with old crushes”), but also backwards from my destination (“which marriages are happy”, “how to raise children”), and look for how the two can connect (“ah, Eve is an old friend from high school who shares this interest in child rearing”).
This is also a technique in math proofs. From XKCD:
Except: sometimes, instead of tricking the grader, you actually just find the correct derivation!
I know someone who successfully used that “handy exam trick” in the International Mathematical Olympiad.
(Of course this isn’t relevant to the actual discussion, but it might amuse you as it amuses me. Further details that I find pleasing: 1. He took care to make sure that the “seam” lay between the end of one page of working and the start of the next. 2. The people marking the script claimed to have found an entirely different error which was not in fact an error, but of course the country’s team leaders didn’t send it back and complain because they knew that if they did the much more serious error in logic was likely to be noticed. For the avoidance of doubt, the person in question was not me.)