The Bellman equation does not apply to bounded rationality
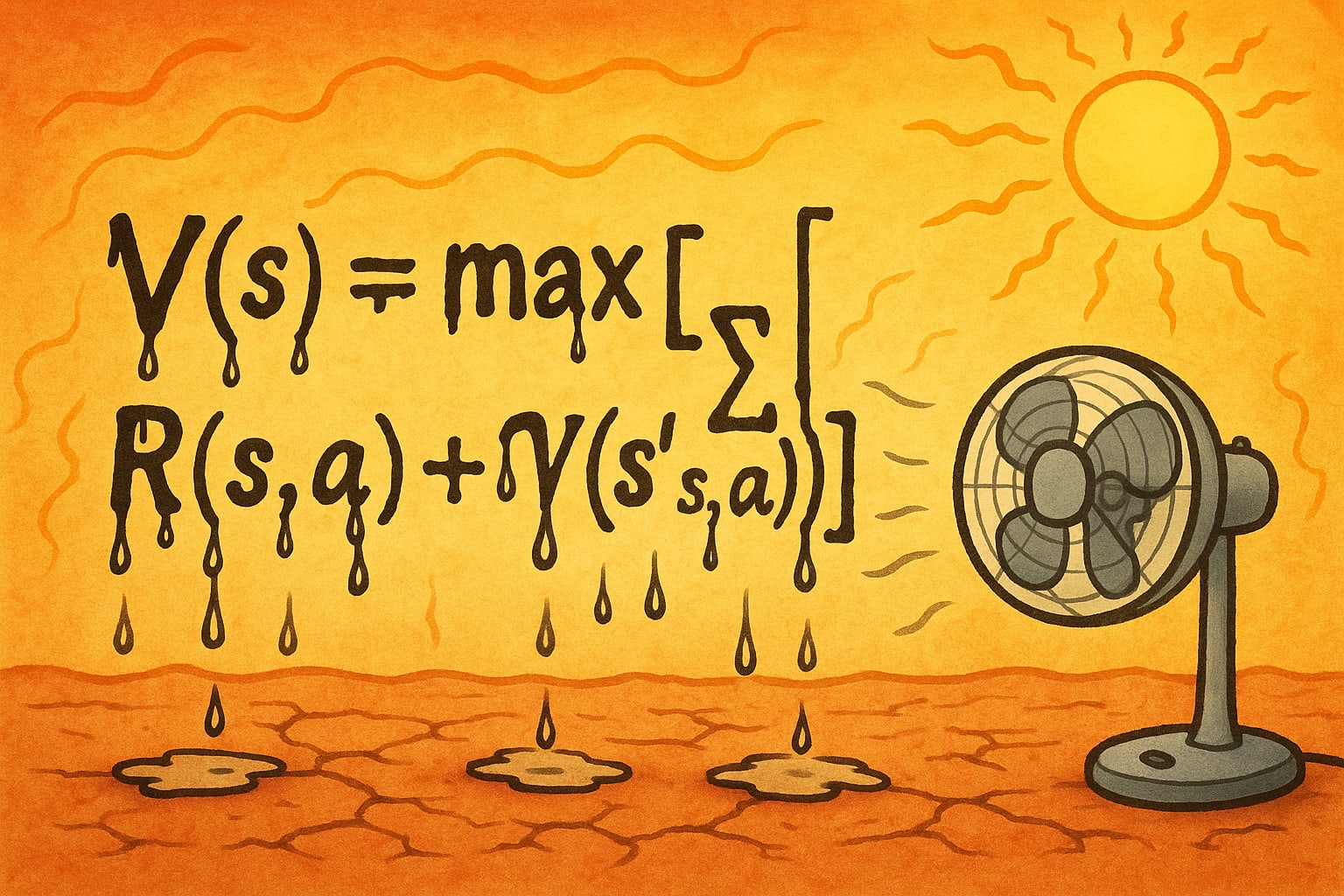
Quick quiz: which of the following is the definition of a rational agent?
An agent who follows the policy with the highest expected utility
An agent who follows the policy of choosing the action with the highest expected utility
Are those even different things? In the case of unbounded rationality, it is a bit of a trick question. Usually (1) is taken as the definition of rational, but according to the Bellman equation, the optimal policy is the one that chooses an optimal action in every state. Seems obvious, right?
Bounded rationality is a form of rationality where the policy must given by an algorithm, and the computational resources used by that algorithm matters. For example, if computation produces heat, than when it is (just for example) extremely unreasonably hot out, the agent might do less computation, or use a computer to do computations for it. (An unbounded rational agent never uses a computer, since it can just simulate computers “in its head”.)
In bounded rationality, (1) and (2) are different, and (2) isn’t even well-defined (there might not be a policy that can always choose the best action, and even if there is that action might depend on the amount of computation that has been done).
So, we cannot say whether a given action is bounded rational, only whether the entire policy is bounded rational.
Example: Guessing a preimage
For example, consider the following problem: given a random 512 bits, guess how many es are in the SHA-3 preimage of those bits.
In the specific case of 3fbef366d350d95ec6ef948dfc2fd1ebd6f1de928c266d86e2ed8e408b2f7b30cad0e14714830369f96ad41c2b58da80bab3bff90a6770910244e28b4f9e80be, you might be tempted to say “32 es”, since you know nothing about that string and 512⁄16 is 32.
However, a better guess is 10, since the preimage is b12ee4ed50edf33e4a388924f35f0190da54ee82ca0338d7dcc4adc3214da21e69d0b0b32789074fef3c05f02d6814da2c8d72057f50835d8f83265e6a4c3b57, which has exactly 10 es.
However, assuming reasonable computational limits, it is unlikely that the optimal policy says 10.b12ee4ed50edf33e4a388924f35f0190da54ee82ca0338d7dcc4adc3214da21e69d0b0b32789074fef3c05f02d6814da2c8d72057f50835d8f83265e6a4c3b57 is just a random string of bits I generated, and for any given random strings of bits, it is unlikely for any given policy (including the optimal policy) to have hard-coded it. There are simply too many possible inputs to hard-code a significant fraction of them! I am guessing that a policy that says 32 es on every input, including b12ee4ed50edf33e4a388924f35f0190da54ee82ca0338d7dcc4adc3214da21e69d0b0b32789074fef3c05f02d6814da2c8d72057f50835d8f83265e6a4c3b57 in particular, is close to optimal.
(Actually formalizing this is too hard for me left as an exercise to the reader. If you do so, I suggest going with a random oracle as a stand-in for SHA-3.)
I’m somewhat confused by the example at the end. SHA-3 (and other hash functions) are not injective, so it’s not at all clear what “the preimage” means here. The example appears to choose a preimage of length 512 bits (matching the output), but SHA-3 is not designed to be injective on that domain either. It almost certainly is not, and therefore also not surjective so that some bitstrings have no such preimage.
It would be possible to restrict the chosen preimages further, e.g. to the lexicographically first preimage, but then just knowing that SHA3(x) = y does not guarantee that x is the preimage as defined.
Maybe a function that is guaranteed to be bijective yet difficult to invert would work better here?
Hmm true. A random permutation oracle I guess? Or “random preimage” of SHA-3?