The Power to Make Scientific Breakthroughs
This is Part IV of the Specificity Sequence
So far, everything we’ve accomplished with our specificity powers has been admittedly kind of destructive: demolishing bad arguments, judging startup ideas as being either definitely bad or only maybe bad… it would be nice to accomplish something more constructive.
Let’s try activating our specificity powers for science. Because at least in science, if we destroy a currently-accepted theory, then it’s a good sign that we’re probably on our way to inventing a better theory!
Choosing Where to Zoom In
In The Power to Demolish Bad Arguments, we zoomed into generic claims by inspecting specific examples of those claims. Actually, “zooming in” is an incomplete description of what we did. There’s a one-to-many relationship between generic claims and specific examples. How do you choose the examples? How do you choose where to zoom into a claim?
It depends if you’re trying to check basic coherence or pinpoint a contradiction.
Checking Basic Coherence
If you’re confused about what the claim even means, you can just try zooming in anywhere to look for any coherent meaning of the claim.
This was our strategy for zooming into Steve’s claim that “Uber exploits its drivers by paying them too little”. We asked Steve to give us any specific example of what he was talking about, and there were none to be found, so the discussion came to an abrupt stop.

Some readers accused me of hunting for the weakest part of Steve’s claim, so I explained in a comment why it’s really not like that:
I’m not saying to hunt for a counterexample that demolishes a claim. I’m saying to ask the person making the claim for a single specific example that’s consistent with the general claim.
Imagine that a general claim has 900 examples and 100 counterexamples. Then I’m just asking to see one of the 900 examples :)
Pinpointing a Contradiction
When a general claim has already shown you plenty of specific examples, but it also has some questionable implications that may be contradictory or nonsensical, that’s when you want to go on the hunt for a counterexample.
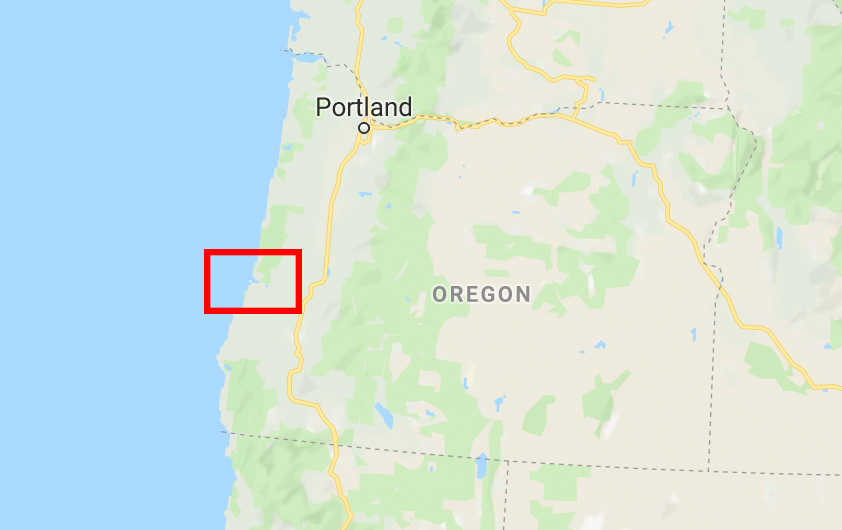
This is how we chose where to zoom into Steve’s claim that “Oregon’s coastline is too straight. I wish all coastlines were less straight so that they could all have a bay!” We purposely chose to zoom in on the most questionable part of Oregon’s coastline, the least straight part, the part that would best contradict his generalization, in order to best help me disambiguate what his point is supposed to be.
Similarly, in “Surely You’re Joking, Mr. Feynman!” (h/t Eliezer), Richard Feynman talks about his trick to check whether a proposed theorem is true by zooming into a specific example designed to pinpoint a contradiction:
I had a scheme, which I still use today when somebody is explaining something that I’m trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they’re all excited. As they’re telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) - disjoint (two halls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn’t true for my hairy green ball thing, so I say, “False!”
If it’s true, they get all excited, and I let them go on for a while. Then I point out my counterexample.
“Oh. We forgot to tell you that it’s Class 2 Hausdorff homomorphic.”
“Well, then,” I say, “It’s trivial! It’s trivial!”
Note that if Feynman were just making up the simplest or most obvious examples, then the proposed theorems would probably always come out true about those examples, because the mathematicians wouldn’t bother using easily-falsifiable theorems as challenges. In order to successfully notice when the proposed theory is false, Feynman must always be picking the craziest examples he can get away with under the mathematicians’ growing list of conditions.
Thought Experiments
In mathematical logic, there’s a formal term for zooming into a theory: model-checking. Given a collection of axioms about sets or numbers or whatever, you probe their implications by looking at specific examples of structures that obey those axioms. Eliezer explains:
Suppose you want to know whether it’s true that all positive integers less than 5, when multiplied by 7, are less than 50. If you prove the general truth that all integers less than 5, times 7, are less than 35, by manipulating the axioms of multiplication and inequality, that’s deduction. If you notice that the only positive integers less than 5 are just {1, 2, 3, 4} and enumerate their products {7, 14, 21, 28}, which are all less than 50, that’s model-checking.
But if we’re doing science, rather than mathematical logic, then zooming into a theory in order to probe its implications is called by a different name: thought experiment.
Say you want to make a revolutionary breakthrough in humanity’s understanding of the age-old concepts of space, time, light, and motion.
What Albert Einstein said was, “Specificity powers, activate! Form of: thought experiment!” And he zoomed into the previously-understood laws of physics so he could get a better view of why they didn’t hold together.

Einstein looked for specific scenarios that would strain the existing theories of his time the most. But he was always careful to stay within the space of scenarios that the existing theories could still reason about, careful not to break any of a theory’s rules or assumptions, but just zooming into the parts that felt to him like loose screws.
He famously described scenarios like riding on a beam of light, or riding a fast-moving train and watching for a lightning flash while other people standing on the platform are watching for it too.
In one famous thought experiment, Einstein imagined a man in a walled room in the setup shown here, and observed that the man wouldn’t be able to distinguish whether his room is fixed in place and he’s in a gravitational field that pulls him leftward (his “down”), or someone is yanking on a rope to accelerate him and the room rightward (his “up”).
Einstein then spent a few years doing hard math to figure out how the laws of physics had to work in order for those two specific situations to be fundamentally equivalent, and the answer he got was his General Theory of Relativity.
What exactly is a “thought experiment” and how does it work? Wikipedia puts it like this:
As opposed to physical experiments, thought experiments do not report new empirical data. They can only provide conclusions based on deductive or inductive reasoning from their starting assumptions. Thought experiments invoke particulars that are irrelevant to the generality of their conclusions. It is the invocation of these particulars that give thought experiments their experiment-like appearance.
Aha, they don’t work by cajoling the universe into giving us new data. All they do is give our brains meaty “particulars”—a.k.a. specifics — to chew on. Thought experiments are yet another demonstration of how specificity makes our brains, and Einstein’s brain, work better.
When I asked Steve about zooming into a strategically-chosen area of Oregon’s coastline and looking at an indented area full of water, that was basically a simple thought experiment to challenge his “Oregon’s coastline is straight” theory. Einstein’s thought experiments were the same thing: zooming into the previously-understood theories of physics so he could get a better view of why they didn’t hold together.
You might think Steve’s statement about Oregon’s coastline was hardly a theory, and it’s too ridiculous to perform a real thought experiment on. But that’s only because we already know that Steve isn’t making sense. Concepts like “phlogiston”, “luminiferous aether”, and even Newtonian gravity are also pretty ridiculous in light of our current scientific understanding, but they’re all still perfectly valid theories to thought-experiment with.
Zooming Out From Specifics
So far, we’ve seen a lot about the power of zooming into specifics. Let’s see the power of starting with a focus on collecting specifics and then zooming out to a general theory.
In the 1830s, many intellectuals were passionately debating the question: Do species of life evolve gradually from other species, or does God put them on Earth in one or more discrete “creation events”?

Charles Darwin had a passion for making observations of the natural world. In his famous 5-year voyage on the H.M.S. Beagle (whose main purpose was supposed to be mapping the coast of South America for the British government), he observed a wide variety of animal species in South America and the Galapagos islands and noted their similarities in detail.
For example, he saw a bunch of Galapagos tortoise species which seemed almost identical to one another, only differing in little traits that made them adapted to their respective environments:

Galápagos tortoises are adapted for different feeding habits. The “saddle-backed” tortoises have shells that rise in the front like a saddle. This adaptation makes it easier for them to lift their necks and feed on taller cactus. “Dome-shaped” tortoises live on islands where most of the vegetation is close to the ground, making it unnecessary for them to raise their heads to feed. Source
Plus, since Darwin also had a passion for geology, he was also digging up fossils and comparing them to the area’s living species. By the time he got back to Britain, he was ready to generalize what he saw:
Species are gradually evolving all the time. There seem to be no discrete creation events.
Next, he wanted to answer another question: What kind of natural process drives species to evolve?
Once again, he set out to collect a bunch of specific observations. He spent a lot of time with British pigeon breeders to understand the specifics of how the breeding process creates new types of of pigeons.

The carrier pigeon (bottom left) and the Brunner pouter (bottom right) were derived from the wild rock pigeon (top). Source
Zooming out from his observations of pigeon breeding, Darwin put forth this generalization:
Some kind of natural force that acts on species the way breeders do would be able to cause the observed evolution of species.
As far as I know, those were Darwin’s breakthroughs leading to the Theory of Evolution by Natural Selection, and they both consist of observing a bunch of specific examples before venturing to zoom out and make a general claim.
(Also, he and Alfred Russel Wallace simultaneously figured out that this “natural breeding force” is a consequence of Thomas Malthus’s observation that all populations are eventually forced to compete for resources.)
So now you have two ways you can activate your specificity powers to help make scientific breakthroughs:
Zoom into existing theories: Take the current theories of your time and think about how they apply to specific hypothetical scenarios in order to understand the contradictions you’ll need to fix with new theories.
Zoom out from specific observations: Make specific observations of a kind of thing in the world until you can generalize a theoretical insight that neatly organizes all the specific stuff you’ve been observing.
Try these out and let us know what you discover.
Next post: The Power to Solve Climate Change
Companion post: Examples of Examples
I have a very different impression how the einstein thought-process worked. There is the issue of how thought experiments can be used to illustrate the findingds and then there is the issue how they were used to generate the findings. To my understanding he thought about all sorts of weird and edge scenarios to explore the rules and then when he found that the theory could not say what happens or that it would say contradictory things that there was reason to suspect it was wrong. He was not suspicous that the theories are wrong and set out to find where but drove them to their limits or even somewhat beyond in order to discover that another theory needs to hold in order to say about the inapplicable territority. And I was of the impression that most of the explorings of the old theory found the old theory to be adequate, although such trips might have served as fuel how to set up a even crazier trip.
For example in the scenario about pulling a rope vs falling I thought that the initial thought process expected that there would be a difference that would point it out. Having diffculty formulating what it would be, would lead to trying to imagine what would be the needed properties. The conceptual analysis leads to suspecting that maybe there is no fact of the matter which situation is which. This all involves a lot of different cognitive processes which is very different from simple “observing” (or is analogous how anything that is analytically provable is “trivial”)
The bit about ridicolousness and thought experiment also has funny connotation to it. Thought experiments are not offensive tools to aim at things you want to destroy. Sure they can wreck theories. But general relativity is a perfectly valid thing to thought experiment with. And in fact because black holes form singularities GR has been “wrecked” by them. GR accepts closed timelike curves examples of which can be thought as thought experiments. And we know that in their current state quantum theories are irreconciable even if they are valid in their own domains. Set up a sitatuation where both have a relevant thing to say and it becomes dicey to say what if anything our current understanding says should happen. Note that shördinger’s cat was supposed to show quantum theory as absurd. Things like aether are not conceptually that inconsistent it’s more that actual experiment speak against them. We knew how to test for the existence of aether pretty staighforwardly and not finding it made us think of crazy alternatives. I t was not the case that aether was found to be conceptually inelegant or silly and I woudl htink it was actually the occam razor favourite. Again demonstarting that a position is faulty is a very different thing from discovering that it is. And the tool is not resricted to tearing down string thoery tries “constructive thought experiment”. If you can tell a story that has basic ontology of strings but which contains the appearance of matter then that could give clues how to setup experiments that would yield otherwise unexpected results.
Thanks, you’re making lots of good points and improvements on the role of thought experiments that I didn’t adequately capture in the post.