Entangled Photons
Previously in series: Decoherence as Projection
Today we shall analyze the phenomenon of “entangled particles”. We’re going to make heavy use of polarized photons here, so you’d better have read yesterday’s post.
If a particle at rest decays into two other particles, their net momentum must add up to 0. The two new particles may have amplitudes to head off in all directions, but in each joint configuration, the directions will be opposite.
By a similar method you can produce two entangled photons which head off in opposite directions, and are guaranteed to be polarized oppositely (at right angles to each other), but with a 50% prior probability of going through any given polarized filter.
You might think that this would involve amplitudes over a continuous spectrum of opposite configurations—an amplitude for photon A to be polarized at 0° and for photon B to be polarized at 90°, an amplitude for A to be 1° polarized and for B to be 91° polarized, etc. But in fact it’s possible to describe the quantum state “unknown but opposite polarizations” much more compactly.
First, note that the two photons are heading off in opposite directions. This justifies calling one photon A and one photon B; they aren’t likely to get their identities mixed up.
As with yesterday, the polarization state (1 ; 0) is what passes a 90° filter. The polarization state (0 ; 1) is what passes a 0° filter. (1 ; 0) is polarized up-down, (0 ; 1) is polarized left-right.
If A is in the polarization state (1 ; 0), we’ll write that as A=(1 ; 0).
If A=(1 ; 0) and B=(0 ; 1), we’ll write that as
[ A=(1 ; 0) ∧ B=(0 ; 1) ]
The state for “unknown opposite polarization” can be written as:
√(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] )
Note that both terms are being multiplied by the square root of 1⁄2. This ensures that the squared modulus of both terms sums to 1. Also, don’t overlook the minus sign in the center, we’ll need it.
If you measure the A photon’s polarization in the up-down/left-right basis, the result is pretty straightforward. Your measurement decoheres the entanglement, creating one evolution out of the A=(1 ; 0) ∧ B=(0 ; 1) configuration, and a second, noninteracting evolution out of the A=(0 ; 1) ∧ B=(1; 0) configuration.
If you find that the A photon is polarized up-down, i.e., (1 ; 0), then you know you’re in the A=(1 ; 0) ∧ B=(0 ; 1) blob of amplitude. So you know that if you or anyone else measures B, they’ll report to you that they found B in the (0 ; 1) or left-right polarization. The version of you that finds A=(1 ; 0), and the version of your friend that finds B=(0 ; 1), always turn out to live in the same blob of amplitude.
On the other side of configuration space, another version of you finds themselves in the A=(0 ; 1) ∧ B=(1; 0) blob. If a friend measures B, the other you will expect to hear that B was polarized up-down, just as you expect to meet the version of your friend that measured B left-right.
But what if you measure the system in a slanted basis—test a photon with a 30° polarized filter? Given the specified starting state, in the up-down / left-right basis, what happens if we measure in the 30° basis instead? Will we still find the photons having opposite polarizations? Can this be demonstrated?
Yes, but the math gets a little more interesting.
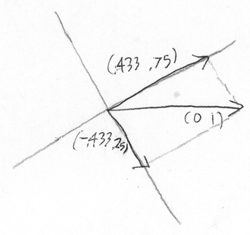
Let’s review, from yesterday, the case where a photon previously polarized in the up-down/left-right basis encounters a 30° filter.
If a photon passes a 0° filter, coming out with polarization (0 ; 1), and then encounters another filter at 30°, the vector that would be transmitted through the 30° filter is
(√3)/2 * (1/2 ; (√3)/2) = (.433 ; .75)
and the polarization vector that would be absorbed is
1⁄2 * (-(√3)/2 ; 1⁄2) = (-.433 ; .25)
Note that the polarization states (1/2 ; (√3)/2) and (-(√3)/2 ; 1⁄2) form an orthonormal basis: The inner product of each vector with itself is 1, and the inner product of the two vectors with each other is 0.
Then we had (√3)/2 of one basis vector plus 1⁄2 of the other, guaranteeing the squared moduli would sum to 1. ((√3)/2)2 + (1/2)2 = 3⁄4 + 1⁄4 = 1.
So we can say that in the 30° basis, the incoming (0 ; 1) photon had a (√3)/2 amplitude to be transmitted, and a 1⁄2 amplitude to be absorbed.
Symmetrically, suppose a photon had passed a 90° filter, coming out with polarization (1 ; 0), and then encountered the same 30° filter. Then the transmitted vector would be
1⁄2 * (1/2 ; (√3)/2) = (.25 ; .433)
and the absorbed vector would be
-(√3)/2 * (-(√3)/2 ; 1⁄2) = (.75 ; -.433)
Now let’s consider again with the entangled pair of photons
√(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] )
and measure photon A with a 30° filter.
Suppose we find that we see photon A absorbed.
Then we know that there was a -(√3)/2 amplitude for this event to occur if the original state had A=(1 ; 0), and a 1⁄2 amplitude for this event to occur if the original state had A=(0 ; 1).
So, if we see that photon A is absorbed, we learn that we are in the now-decoherent blob of amplitude:
( -(√3)/2 * √(1/2) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(0 ; 1) ] )
- ( 1⁄2 * √(1/2) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1; 0) ] )
You might be tempted to add the two amplitudes for A being absorbed—the -(√3)/2 * √(1/2) and the −1/2 * √(1/2)—and get a total amplitude of -.966, which, squared, comes out as .933.
But if this were true, there would be a 93% prior probability of A being absorbed by the filter—a huge prior expectation to see it absorbed. There should be a 50% prior chance of seeing A absorbed.
What went wrong is that, even though we haven’t yet measured B, the configurations with B=(0 ; 1) and B=(1 ; 0) are distinct. B could be light-years away, and unknown to us; the configurations would still be distinct. So we don’t add the amplitudes for the two terms; we keep them separate.
When the amplitudes for the terms are separately squared, and the squares added together, we get a prior absorption probability of 1/2—which is exactly what we should expect.
Okay, so we’re in the decoherent blob where A is absorbed by a 30° filter. Now consider what happens over at B, within our blob, if a friend measures B with another 30° filter.
The new starting amplitude distribution is:
( -(√3)/2 * √(1/2) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(0 ; 1) ] )
- ( 1⁄2 * √(1/2) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1; 0) ] )
In the case where B=(0 ; 1), it has an amplitude of (√3)/2 to be transmitted through a 30° filter; being transmitted through a 30° filter corresponds to the polarization state (1/2 ; (√3)/2). Likewise, a 1⁄2 amplitude to be absorbed (polarization state (-(√3)/2 ; 1⁄2).)
In the case where B=(1 ; 0) it has an amplitude of 1⁄2 to be transmitted with state (1/2 ; (√3)/2). And an amplitude of -(√3)/2 to occupy the state (-(√3)/2 ; 1⁄2) and be absorbed.
So add up four terms:
( -(√3)/2 * √(1/2) ) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(0 ; 1) ]
breaks down into
( -(√3)/2 * √(1/2) ) * (√3)/2 * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1/2 ; (√3)/2) ] +
( -(√3)/2 * √(1/2) ) * 1⁄2 * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(-(√3)/2 ; 1⁄2) ]
and
- ( 1⁄2 * √(1/2) ) * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1; 0) ] )
breaks down into
-( 1⁄2 * √(1/2) ) * 1⁄2 * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1/2 ; (√3)/2) ] +
-( 1⁄2 * √(1/2) ) * -(√3)/2 * [ A=(-(√3)/2 ; 1⁄2) ∧ B=(-(√3)/2 ; 1⁄2) ]
These four terms occupy only two distinct configurations.
Adding the amplitudes, the configuration [ A=(-(√3)/2 ; 1⁄2) ∧ B=(-(√3)/2 ; 1⁄2) ] ends up with zero amplitude, while [ A=(-(√3)/2 ; 1⁄2) ∧ B=(1/2 ; (√3)/2) ] ends up with a final amplitude of √(1/2).
So, within the blob in which you’ve found yourself, the probability of your friend seeing that a 30° filter blocks both A and B, is 0. The probability of seeing that a 30° filter blocks A and transmits B, is 50%.
Symmetrically, there’s another blob of amplitude where your other self sees A transmitted and B blocked, with probability 50%. And A transmitted and B transmitted, with probability 0%.
So you and your friend, when you compare results in some particular blob of decohered amplitude, always find that the two photons have opposite polarization.
And in general, if you use two equally oriented polarization filters to measure a pair of photons in the inital state:
√(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] )
then you are guaranteed that one filter will transmit, and the other filter absorb—regardless of how you set the filters, so long as you use the same setting. The photons always have opposite polarizations, even though the prior probability of any particular photon having a particular polarization is 50%.
What if I measure one photon with a 0° filter, and find that it is transmitted (= state (0 ; 1)), and then I measure the other photon with a 30° filter?
The probability works out to just the same as if I knew the other photon had state (1 ; 0)—in effect, it now does.
Over on my side, I’ve decohered the amplitude over the joint distribution, into blobs in which A has been transmitted, and A absorbed. I am in the decoherent blob with A transmitted: A=(0 ; 1). Ergo, the amplitude vector / polarization state of B, in my blob, behaves as if it starts out as (1 ; 0). This is just as true whether I measure it with another 0° filter, or a 30° filter.
With symmetrically entangled particles, each particle seems to know the state the other particle has been measured in. But “seems” is the operative word here. Actually we’re just dealing with decoherence that happens to take place in a very symmetrical way.
Tomorrow (if all goes according to plan) we’ll look at Bell’s Theorem, which rules out the possibility that each photon already has a fixed, non-quantum state that locally determines the result of any possible polarization measurement.
Part of The Quantum Physics Sequence
Next post: “Bell’s Theorem: No EPR ‘Reality’”
Previous post: “Decoherence as Projection”
- The Quantum Physics Sequence by (11 Jun 2008 3:42 UTC; 77 points)
- Bell’s Theorem: No EPR “Reality” by (4 May 2008 4:44 UTC; 40 points)
- And the Winner is… Many-Worlds! by (12 Jun 2008 6:05 UTC; 30 points)
- Decoherence as Projection by (2 May 2008 6:32 UTC; 27 points)
- Spooky Action at a Distance: The No-Communication Theorem by (5 May 2008 2:43 UTC; 22 points)
- An Intuitive Explanation of Quantum Mechanics by (12 Jun 2008 3:45 UTC; 18 points)
- Quantum Physics Revealed As Non-Mysterious by (12 Jun 2008 5:20 UTC; 13 points)
- [SEQ RERUN] Entangled Photons by (24 Apr 2012 4:04 UTC; 6 points)
- 's comment on Kickstarting the audio version of the upcoming book “The Sequences” by (29 Dec 2014 20:38 UTC; 2 points)
- 's comment on Designing Rationalist Projects by (15 May 2011 17:06 UTC; -59 points)
Ah! Now I get why having distant paired particles doesn’t let you communicate faster than light. This stuff is gold.
“a total amplitude of .965”—wouldn’t it be ‘-.966’? Trivial, but if it’s going in the book...
I must admit that I’m only managing to follow about 75% of your arguments. Still, I’m slowly building up a mental model of what entanglement is really all about that’s substantially different than what I had before.
I know that this model is superior because, for the first time, the concept of entangled photon holes doesn’t appear to be meaningless nonsense.
Does the “world” in “many worlds” refer to the same thing as “blob” in this post?
Yes.
This post (together with the previous one) left me in a quite a bit of a confusion. How does this model with polarization vectors correspond to the old “amplitude distribution over a configuration space of «a photon here and a photon there»”? What are the configurations here, and when are they distinct? (And it seems I am not the only one who got confused by this.)
I think, I found the solution; the photons have a distinguishing property: spin. So, if configurations are more like “a photon with a +1 spin here, a photon with a −1 spin there...”, then it all fits nicely in the same model. And the amplitude distribution corresponding to the situation described in the article would be:
(modulo a constant factor). Where |p+> (a photon with a +1 spin at P) corresponds to the P=(1 ; i) and |p-> to the P=(1 ; -i) in the article’s notation. Of course, the math remains the same, but now I can see a bit more clearly the amplitude distribution and what are the distinct configurations.
Hmm, it’s nice that there is this pretty compact formulation for two coupled but separately “unpolarized” photons. But, this still leaves me with a question of how does one “unpolarized” photon (a photon for which half of the squared amplitude would pass any polarized filter) looks like?
I would guess that there is no such thing. We might be ignorant about the photon’s polarization, but it does have some definite polarization even before it passes any filter. Otherwise, it has to be in a similarly tangled state with something (eg. its source).
Hmm, how would I check this?..
You can construct a photon that will pass any linear polarization filter 50% of the time, by constructing a circular polarization photon. If you include arbitrary polarizing filters including elliptical polarization, then yes, you will need to have a 2-or-more-particle entangled state to get 50% regardless of filter.
Having 2 or more particles entangled is of course the overwhelmingly normal case. If you take photons from an incandescent lightbulb and attenuate the signal until you’re counting photons, then half of them will pass any polarizing filter you can construct (not counting inefficiencies in the polarizer, obviously).
You’re right. Such a thing is not expressible as a wavefunction, as an unentangled pure state. Entanglement with something else that you are ignorant of (unentangled with) is one way of getting the right statistics. So too is expressing it as an impure state in the density matrix formalism. Some people appeal to the “church of the larger Hilbert space”, saying that only pure states exist, and that system is entangled with other, unobservable ones.
The state for “unknown opposite polarization” can be written as: √(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] )
I don’t follow. I have no idea where this equation is coming from and how to interpret it. Can anyone make me understand this, please?
Hm. I can try (depending on how math-y and/or patient you are I may also fail; this is quite long).
In the spirit of Eliezer’s dictum “rather than a 3-vector being made out of an ordered list of 3 scalars, a 3-vector was just a pure mathematical object in a vector algebra” the same thing is going on here—the configuration of the photon is given by a complex 2-vector, which we represent as a pair of complex numbers. This means that we have chosen a basis - to quote previous post again “We can represent the polarization of light as a complex amplitude for up-down plus a complex amplitude for left-right”. Thus, the basis is a pair of configurations—first one being “up-down”, the second one being “left-right”. Any other configuration of a single photon is a linear combination of those—hence we write it as (1 ; 0) or (0 ; -i) or (√.5 ; √.5).
There is an unfortunate complication that two configurations are identified if they differ by a scalar complex factor. So as long as you talk about just one photon configurations (0 ; -i) and (0, 1) are actually the same.
(Side note: One has to be careful with this issue when talking about multiple photons (as we will shortly); in that case only one overall scalar complex factor for the whole joint system is allowed, as opposed to “one for each photon,” which does not even make sense, because “each photon” does not necessarily make sense—due to entanglement. I’ll get back to this after I talk about how one describes a joint configuration for multiple systems, which is right after this.)
What about a configuration of two photons? Or in general, a combined quantum system describing joint configurations of (system number 1) and (system number 2)? The technical term here is “tensor product”, a term Eliezer is careful to avoid (because math). In concrete terms, you can take all combination of basis configurations as a basis for the joint configuration space. In the case of two photons and using our basis “up-down”=(1 ; 0) and “left-right”=(0 ; 1) we get 4 basis configurations for the joint system: (1 ; 0) ∧ (1 ; 0) , (1 ; 0) ∧ (0 ; 1), (0 ; 1) ∧ (0 ; 1) and (0 ; 1) ∧ (1 ; 0). Every joint configuration can be described as a complex linear combination of these. Hence it makes sense to write for a joint state something like √(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] ).
Some of these are “plaid” or “factored” configurations—notably each of the 4 basis configurations are “product”, but there are some other ones—you can take (√.5 ; √.5) ∧ (1,0) and this is also a product. The rules of the game encoded in the words “tensor product” say that (√.5 ; √.5) ∧ (1,0)= (√.5 ; 0) ∧ (1,0)+ (0 ; √.5) ∧ (1,0)= √.5 ( 1 ; 0) ∧ (1,0)+ √.5 (0 ;1)∧ (1,0), so this is indeed a linear combination of two “basic” configurations ( 1 ; 0) ∧ (1,0) and (0 ;1)∧ (1,0). Note that written this way it does not look factored, or “plaid”, but it is. It is a factored as (√.5 ; √.5) ∧ (1,0). Now it is a mathematical fact that there are combinations that can not be rewritten in a factored form, that are actually “entangled”—and √(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] ) is one such.
Side note #2: Now I can explain about that “one complex scalar factor” business. For a factored configuration (a,b)∧(c,d) we can multiply each factor by a scalar (ka, kb)∧(lc, ld)= k(a,b)∧l(c,d)=(kl) (a,b)∧(c,d) and this differs by a single scalar multiplication by (kl) from (a,b)∧(c,d), so is the same joint configuration. However for (a,b)∧(c,d) + (e,f)∧(c,d) we can not multiply each of the copies of (c,d) by it’s own scalar - (a,b)∧(k c, k d) + (e,f)∧(l c, ld) is not equivalent to (a,b)∧(c,d) + (e,f)∧(c,d) in the joint configuration space. Hence the caveat.
Returning to our main line, one may ask why √(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] )? Why does this particular combination encode “unknown opposite polarization”? First of all we need to understand what “same” or “opposite” polarization means. “Same” known state means that the state is factoriseable as (a,b)∧(a,b) - “both in the same known configuration (a,b)”. This is of course the same as (a,b)∧(ka,kb)=k (a,b)∧(a,b), because of the constant scalar rule. What does “opposite” mean? Well, the opposite of (1 ; 0) is (0 ; 1), and in general the opposite known configuration means that the configuration is factorizeable as (a,b)∧(c,d) where (a,b) and (c,d) are (Hermitian) orthogonal. (“Hermitian” because all entries are complex; this is an extension of usual “orhtogonal” property that we know from real vectors.)
√(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] ) is not a factorizeable configuration, so it’s not known opposite polarization, but it’s a mixture of two such. This still does not explain why this is the “unknown mixed state”. Why the—sign, for example? One “naive” justification is that it works. Clearly in the decohered blob where you have A=(1 ; 0) you also have B=(0 ; 1) and vice versa. But you can decohere this joint configuration in a different way and still get similar outcome - this is what Eliezer’s post demonstrates. But there is a more high-brow reason.
The more high brow reason is that the joint configuration space—the span of (1 ; 0) ∧ (1 ; 0) , (1 ; 0) ∧ (0 ; 1), (0 ; 1) ∧ (0; 1) and (0 ; 1) ∧ (1 ; 0) - has a decomposition into a “symmetric” and “antisymmetric” parts. The antisymmetric part is spanned by u∧v-v∧u for any pair of configurations u, v, and the symmetric part is spanned by v∧v, u∧u and v∧u+u∧v. In particular the antisymmetric part is the one where the configuration is in the “unknown but opposite polarization”. The important thing is that this is a 1-dimensional subspace, so all configurations in it are the same, up to a scalar multiple. So you can use any v and u and you always get the same result. And if you use u=(0 ; 1) and v=(1 ; 0) you get exactly √(1/2) * ( [ A=(1 ; 0) ∧ B=(0 ; 1) ] - [ A=(0 ; 1) ∧ B=(1; 0) ] ), where √(1/2) is a scalar chosen to make the norm equal 1. But of course if you decohere u∧v-v∧u “along u” you will a blob where A=u and B=v and a blob where A=v and B=u. So no matter which way you decohere this one joint configuration you will always get opposite individual configurations! Math works!
Side note 3: If photons were not moving in opposite directions we would have a problem—photons are bosonic, so a joint configuration space would actually only contain the symmetric part, not the antisymmetric part (that’s sort of what “bosonic” means). However, this whole discussion is actually happening inside a larger joint configuration space where we have tensored with the space of positions/momenta of the photons, in addition to polarizations, and there the two photons have different configurations, so everything should be ok. Say the position configuration of first photon is described by f, and the second by g. If I did everything correctly the “total unknown opposite polarization configuration” is [(u∧f) ∧ (v∧g) + (v∧g)∧(u∧f)] - [(u∧g) ∧ (v∧f) + (v∧f)∧(u∧g)] isomorphic to [(u∧v) - (v∧u)] ∧ [(f∧g)-(g∧f)], which is symmetric in (u∧f), (v∧g) as it should be, but antisymmetric in u,v and g, f separately.
I’m having an incredibly difficult time following this. I’ve understood- or at least thought I understood most of the sequence thus far, but this post in particular is really rough.
Perhaps that is just a matter of having substantial amounts of actual math in front of me where I expect lesswrong posts to be shiny and easy to digest? To become stronger one must challenge oneself, and most of the posts on this site go down smooth.
That is a trade off of making a subject more approachable: when it becomes less shiny it is much harder to retain interest. Lesswrong is very, very shiny indeed. Then again I probably wouldn’t have had such interest in quantum mechanics otherwise, so maybe this is simply where the rubber really hits the road.