Alternative Models of Superposition
Zephaniah Roe (mentee) and Rick Goldstein (mentor) conducted these experiments during continued work following the SPAR Spring 2025 cohort.
Disclaimer / Epistemic status: We spent roughly 30 hours on this post. We are not confident in these findings but we think they are interesting and worth sharing.
We assume some basic familiarity with the superposition hypothesis from Elhage et al., 2022, but have an additional “Preliminaries” section below to provide background.
Summary
Toy Models of Superposition (2022)—which we call TMS for short—demonstrates that a toy autoencoder can represent 5 features in a rank 2 matrix. In other words, the paper shows that models can represent more features than they have dimensions. While the original model proposed in the paper has since been extensively studied, there are alternative toy models which may give different results. In this post, we use a loss function that focuses only on reconstructing active features and find that this variation allows us to squeeze dozens of features into two dimensions without a non-linearity.
We do not claim to find anything extraordinary or groundbreaking. Rather, we attempt to challenge two potential assumptions about superposition that we don’t believe hold universally:
Assumption #1: The number of features represented in a space is bounded above by the number of almost-orthogonal[1] vectors that fit in that space.
TMS makes a related claim which is less strong: “Concretely, in the superposition hypothesis, features are represented as almost-orthogonal directions in the vector space of neuron outputs.”
Assumption #2: Element-wise non-linearities perform the computation which makes superposition possible.
TMS claims that superposition “doesn’t occur in linear models.”
In this post, we show empirically that neither of these claims is universally true by designing toy models where they no longer hold.
Preliminaries
TMS introduces a model that, despite consisting of only 15 trainable parameters, is intriguingly complex. The model is defined by where and . The authors show that when is sparse enough (i.e., the probability that is high), the model can represent five features even though .
When sparsity is sufficiently high, the probability that more than one input feature will be present is extremely low. If there is a 5% chance that each is non-zero, there is ~2% chance that more than one feature will be active but a ~20% chance that only one feature will be present. This means that the vast majority of non-zero inputs to the model will have a single feature present.
Consider input . Calculating will give us the second column of the matrix. Then, when we take , we are computing the dot product of the second column with every other column in . Assuming that the vector length of each column in is the same, the most active output will be the second feature (this is just a property of the dot product). The same logic applies if the non-zero feature is any positive value.
When you train the original model from TMS, it does not always represent all five features, but when it does, the results can be remarkably clean. In the figure below, we show the five columns of the weight matrix, each as a direction in two-dimensional space. We assign each color to a feature. For example, the direction of the second feature’s weights is represented as a blue arrow. Areas in the hidden layer that result in the second feature having the highest output are shown in a lighter blue. Finally, the dark blue dot marks the location in the hidden space that maps to.
If you view this toy model as a kind of classifier, then the colored areas above represent a kind of classification boundary for the latent space of the model.
Role of Non-linearities
When the toy model described above represents features in superposition, there is the opportunity for interference. Concretely, when we pass to the model, we won’t get a one-hot vector. The second output will be the highest, but the other outputs will give other positive or negative values.
The negative output values correspond to features with weights that point in an opposite direction from the second feature in vector space. In TMS, the model is trained with a mean squared error loss, meaning these negative values are quite costly when they should be zero. The ReLU non-linearity conveniently filters these negative values, allowing for non-orthogonal representation of features without high reconstruction loss. In the linear case, however, the interference cannot be eliminated so superposition is extremely costly. We claim that for the TMS model described above, the ReLU doesn’t do computation as much as it makes interference less punishing. In other words, the model doesn’t use the ReLU to learn a non-linear rule. Rather, it removes the negative values which are especially punishing to the reconstruction loss.
This suggests we don’t need the ReLU at all: ReLUs help bring loss closer to 0, but don’t help identify the maximum feature.[2]Any training objective that values accurate representation of active features over tolerating noise from non-orthogonal representations should represent features in superposition.
Alternative Model of Superposition
We show that you can have superposition with no element-wise non-linearity and a different loss. We change the original TMS setup to have no ReLU and more features. We initialize and such that the model takes 100 inputs rather than 5. During training, every example includes a single target where the target input is sampled from a uniform distribution between 0 and 1. We let there be a probability that every other feature will also be present. Non-target features which are selected are sampled uniformly between 0 and 0.1. Next, we change the reconstruction loss to only include the target class rather than the entire output:[3]
Note that this gives us a model that appears to be entirely linear. The “magic” here is the ability to select only a single term in the loss, but this is not a non-linearity in the traditional sense. Another perspective is that the loss above includes an implied selection or maximum at the end of the network that filters the noise from superposition and serves as a covert non-linearity. We believe it is still appropriate to call this model “linear” but note that the loss is doing some heavy lifting.
If we let , there is more than a 99% chance that at least one of the 99 non-target features will be nonzero. This means that although the loss focuses on the target input, the model still has to handle the interference cost of non-target input features. In this setup, despite having some interference on almost all training examples, the model does a reasonably good job of representing some direction for all 100 features:
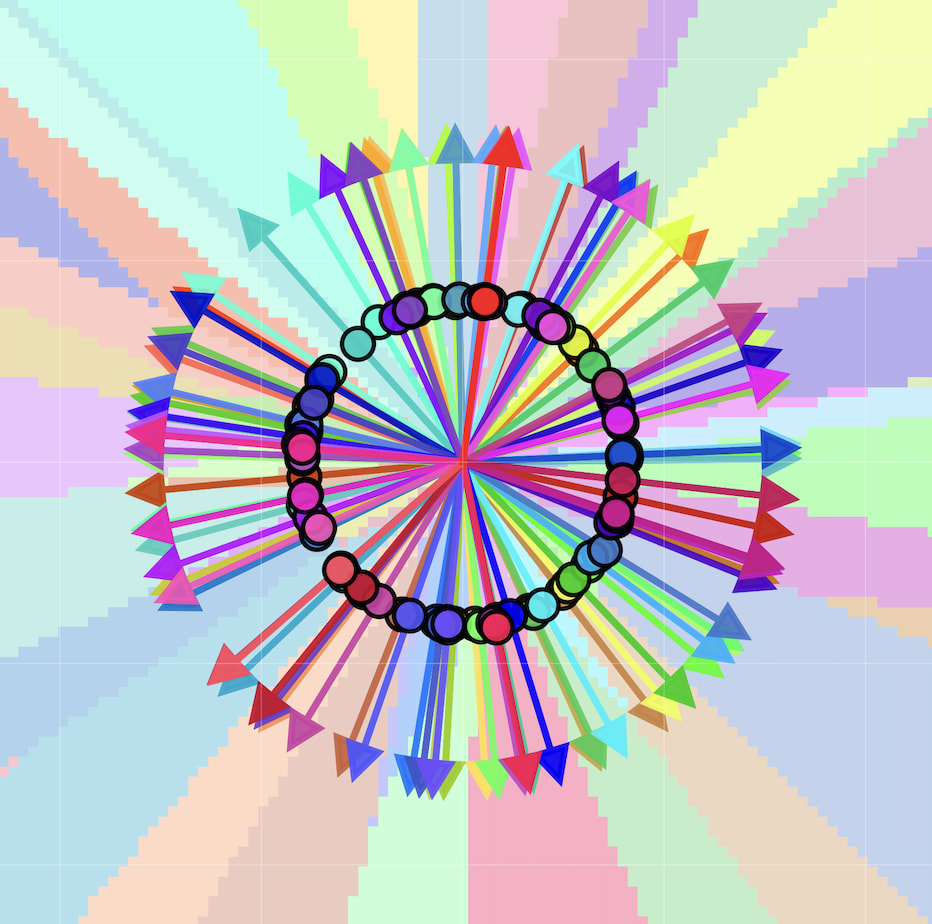
We evaluate the classification accuracy of the model by taking a one-hot vector for each input feature and feeding it to the model. If the top output is the same class as the target feature, we say the model represents the target “accurately.” In the above figure, the model represents 31 classes accurately. Incorrect classifications happen when there is a weight vector that is adjacent in the vector space but is slightly longer than the weight vector for the target feature.
By increasing sparsity, you can increase the classification accuracies of the model. At , it is fairly easy to accurately represent more than 50 features. However, when is higher, it is much harder to get results as clean as the example shown above.
Implications
Superposition, Memorization, and Double Descent contains some figures that appear similar to this post, but are different in important ways. The paper shows that under some conditions, models can memorize arbitrary numbers of data points (relevant code from the paper here). Our experiments, however, focus on representations of features, rather than datapoints. Our setup is designed such that there is some interference on all training examples and, in some cases, gradients will lead the model in the wrong direction. Despite this, the model learns the underlying structure of the data.
Our findings may have implications for techniques that decompose latent activations (e.g., Bricken et al., 2023) or weights (e.g., Bushnaq et al., 2025). These techniques face the potential issue of not being able to safely determine the maximum number of features, circuits, etc. to look for.
The experiment also highlights the importance of studying a more diverse set of toy models. Slightly different assumptions produce wildly different models, so it is important to track which design choices are relevant to reproduce which results. In our example, we show that non-linearities are essential to superposition only given certain assumptions about the loss function. Researchers should be cautious when claiming results from toy models hold generally.
Once again, these experiments were done quickly and don’t reflect the rigor of a paper or preprint. We are happy to be proven wrong by those who have thought deeply about this topic.
Zephaniah Roe (mentee) and Rick Goldstein (mentor) conducted this experiment following the SPAR Spring 2025 cohort. Rick suggested the heatmap-style explanation for toy models which was essential for making the insights in this post. Zephaniah conducted the experiments, made key insights and wrote this post.
- ^
For a concrete definition of “almost-orthogonal,” see the Superposition Hypothesis section of TMS.
- ^
In a deep network, bringing activations to 0 can remove interference, so we don’t claim that ReLU are always unnecessary. In fact, ReLUs almost certainly learn non-linear rules in addition to filtering noise.
- ^
This loss is admittedly less conventional than a traditional mean squared error loss. We do note that losses like cross entropy use only the target class probability which was part of our motivation. The and Carlini-Wagner losses do something somewhat analogous as well.
The restriction of the loss to the target feels like cheating, to be honest. The linear model claim is scoped to reconstruction loss, where you genuinely don’t see superposition as far as i’m aware. And in this case, the reconstruction loss would be poor, because the vectors are nested so close to each other that adjacent features false fire.
I agree with the core point about finding alternative models of superposition though. As far as I know, there is no evidence that the Toy Model paper is accurate to how real models actually represent things, except at the broadest level. Towards Monosemanticity in fact notes divergence from the Toy Model paper (see Feature Splitting).
On the model itself, for p=0.0, and p=1.0, why can’t you place vectors equidistant around the circle, allowing for arbitrarily many features?
To your point about the loss, I believe it’s absolutely correct that this is an entirely different setting than the linear models from TMS. I wouldn’t characterize this as cheating, because it feels entirely possible that models in practice have an effective mechanism for handling lots of interference, but admittedly, the fact that you only select the target feature is the difference that makes this experiment work at all.
If I understand this question correctly, for p=0.0 it should be possible to have arbitrarily many features. In this setting, there is no possibility for interference so if you tune hyperparameters correctly, you should be able to get as many features as you want. Empirically, I didn’t find a clear limit but, at the very least I can say that you should be able to get “a lot.” Because all inputs are orthogonal, in this case, the results should be very similar to Superposition, Memorization, and Double Descent.
p=1.0 would be an interesting experiment that I didn’t run, but if I had to guess, the results wouldn’t be very clean because there would be quite a bit of interference on each training example.
I guess I mean cheating purely as “I don’t think this applies to to the Toy Model setting”, as opposed to saying it’s not a potentially valuable loss to study.
For p=1.0, I forgot that each of the noise features are random between 0 and 0.1, as opposed to fixed magnitude. The reason I brought it up is because if they were fixed magnitude 0.05 then they would all cancel out and face in the opposite direction to the target feature with magnitude 0.05. Now I reread the setting again I don’t think that’s relevant, though.
This is a very interesting thought! I think your intuition is probably correct even though it is somewhat counterintuitive. Perhaps I’ll run this experiment at some point.
Let me know if you do. I keep changing my mind on what the outcome would be lol.
Reposting my Slack comment here for the record: I’m excited to see challenges to our fundamental assumptions and exploration of alternatives!
Unfortunately, I think that the modified loss function makes the task a lot easier, and the results not applicable to superposition. (I think @Alex Gibson makes a similar point above.)
It is much easier to reconstruct the active feature without regard for interference (inactive features also appearing active).
In general, I find that the issue in NNs is that you not only need to “store” things in superposition, but be able to read them off with low error / interference. Chris Olah’s note on “linear readability” here (inspired by the Computation in Superposition work) describes that somewhat.
We’ve experimented with similar loss function ideas (almost the same as your loss actually, for APD) at Apollo, but always found that ignoring inactive features makes the task unrealistically easy.
This seems deeply connected to Modern Hopfield Networks, which have been able to achieve exponential memory capacity relative to the number of dimensions, compared to the linear memory capacity of traditional Hopfield networks. The key is the use of the softmax nonlinearity between the similarity and projection steps of the memory retrieval mechanism, which seems like an obvious extension of the original model in hindsight. Apparently, there is a lot of mathematical similarity between these memory models and the self-attention layers used in Transformers.
What you’re looking at is also closely related to the near-orthogonality property of random vectors in high-dimensional space, which is a key principle behind hyperdimensional computing / vector-symbolic architectures. So-called hypervectors (which may be binary, bimodal, real-valued, complex-valued, etc.) can be combined via superposition, binding, and permutation operations into interpretable data structures in the same high-dimensional space as the elemental hypervectors. The ability to combine into and extract from superposition is key to the performance of these models.
As dimensionality D of your space increases, the standard deviation of the distribution of inner products of pairs of unit vectors sampled uniformly from this space falls off as σ=1/√D:
In other words, for any given threshold of “near-orthogonality”, the probability that any two randomly sampled (hyper)vectors will have an inner product with an absolute value smaller than this threshold grows to near-certainty with a high enough number of dimensions. A 1000-dimensional space effectively becomes a million-dimensional space in terms of the number of basis vectors you can combine in superposition and still be able to tease them apart.