Selective regularization for alignment-focused representation engineering

We study how selective regularization during training can guide neural networks to develop predictable, interpretable latent spaces with alignment applications in mind. Using color as a test domain, we observe that anchoring even a single concept (red) influences the organization of other concepts, with related concepts clustering nearby — even with weak supervision. We then propose that concept-anchored representation engineering might enable more precise intervention in complex models without requiring extensive post-hoc interpretability work.

Still frame from a visualization of the evolution of the latent space of our experiment model. This image has been tightly cropped to show only a thin slice of the full frame. It shows three vibrant, colorful scatter plots, the left resembling a cube, and the other two suggesting a manifold in high-dimensional space.

Introduction

In our previous post, we proposed that anchoring key concepts to specific directions in latent space during training might make AI systems more interpretable and controllable. This post presents our exploratory findings as we work toward that goal, adapting and combining techniques from representation learning with a specific focus on alignment applications.

Rather than attempting to discover and modify latent directions after training (as in mechanistic interpretability), we’re exploring whether it’s possible to impose useful structure on latent spaces during training, creating a more interpretable representation from the start. Many of the techniques we use have precedents in machine learning literature, but our focus is on their application to alignment challenges and whether they might enable more controlled model behavior.

Using color as an experimental domain, we investigated whether simple autoencoders with targeted regularization could learn predictable latent space structures that organize concepts in ways we can understand and potentially control — with specific colors as a stand-in for “concepts”^[1].

By intentionally structuring a portion of the model’s internal representations during training, we aimed to know exactly where key concepts will be embedded without needing to search for them. Importantly, we don’t constrain the entire latent space, but only the aspects relevant to concepts we care about. This selective approach allows the model to find optimal representations for other concepts while still creating a predictable structure for the concepts we want to control. We observed that other concepts naturally organized themselves in relation to our anchored concepts, while still maintaining flexibility in dimensions we didn’t constrain.

Our experiments incorporate elements from established techniques in representation learning, prototype-based models, and supervised autoencoders, but with a specific adaptation: using stochastic, selective regularization with minimal concept anchoring (just a single concept) to influence broader representation organization without dictating the entire structure. We view this work as preparatory research for developing techniques to train more complex models in domains in which data labelling is hard, such as language.

In this post, “we” refers to “me and Claude 3.7 Sonnet,” who helped draft this content. The underlying research was conducted with coding assistance from Gemini 2.5 Pro, GPT-4o, and GPT-4.1, and literature review by deep research in ChatGPT.

Related work

Our approach builds upon several established research directions in machine learning. Concept Activation Vectors (CAVs)^[2] pioneered the identification of latent space directions corresponding to human-interpretable concepts, though primarily as an interpretability technique rather than a training mechanism. Work on attribute-based regularization^[3] has shown that variational autoencoders can be structured to encode specific attributes along designated dimensions, while our work applies to simple autoencoders with no assumption of monosemantic representations. Recent research has also explored using concept vectors for modifying model behavior through gradient penalization in latent space^[4]. Our work differs by proactively anchoring concepts during training rather than analyzing or modifying latent representations post-hoc.

Several approaches have explored similar ideas through different frameworks. Supervised autoencoder methods often incorporate geometric losses that fix class clusters to pre-determined coordinates in the latent space^[5]. Similarly, center loss for face recognition trains a “center” vector per class and penalizes distances to it^[6]. Prototypical VAE uses pre-set “prototype” anchors in latent space to distribute regularization^[7]. These techniques all employ concept anchoring in some form, though our approach is distinctive in focusing specifically on the minimal supervision needed and examining how structure emerges around it rather than explicitly defining the entire latent organization.

In the contrastive and metric learning literature, techniques like supervised contrastive learning^[8] cause samples of the same class to cluster together, but typically don’t pin clusters to particular locations in advance. These methods achieve similar grouping of related concepts but don’t provide the same level of predictability and control over where specific concepts will be represented. In unsupervised contrastive learning (e.g. SimCLR^[9]/BYOL^[10]), the clusters emerge solely from data similarities, with no predefined anchor for a concept.

Alignment motivation

Our interest in these techniques stems specifically from challenges in AI alignment. Current approaches like RLHF and instruction tuning adjust model behavior without providing precise control over specific capabilities. Meanwhile, mechanistic interpretability requires significant post-hoc effort to understand models’ internal representations, with limited guarantees of success.

We’re exploring whether a middle path exists: deliberately structuring the latent space during pre-training to make certain concepts more accessible and controllable afterward. This approach is motivated in part by findings on critical learning periods in neural networks^[11], which demonstrated that networks lose plasticity early in training (even in the first few epochs!), establishing connectivity patterns that become increasingly difficult to reshape later.

Recent work on emergent misalignment further strengthens the case for latent space structure, showing that models fine-tuned solely to write insecure code subsequently exhibited a range of misaligned behaviors in unrelated contexts, from expressing anti-human views to giving malicious advice^[12]. This suggests that even highly abstract related concepts naturally cluster together in latent space, making the organization of these representations a critical factor in alignment. Deliberately structuring these representations during pre-training may provide more direct control than purely post-hoc interventions.

If models develop more predictable representations for key concepts we care about (like harmfulness, deception, or security-relevant knowledge), we might gain better tools for:

Monitoring the presence of specific capabilities during training
Selectively intervening on specific behaviors without broad performance impacts
Creating more fundamental control mechanisms than prompt-level constraints.

While our experiments with color are far simpler than language model alignment challenges, they provide a testbed for techniques that might eventually scale to more complex domains.

Color as a test domain

We chose color as our initial experimental domain because it offers several properties that make it suitable for exploring latent space organization:

Clear ground truth: Every color has objective RGB values that can be precisely measured, so we can check whether our manipulations of latent space produce the expected results.
Hierarchical and multidimensional structure: Primary colors (red, green, blue) combine to form secondary colors (yellow, cyan, magenta), which further mix together and with black and white to create continuous hues, tones, and shades. This hierarchical relationship may mirror how abstract concepts relate in more complex domains.
Visually intuitive: We can directly see the organization of the latent space and understand what’s happening. When we visualize embeddings of colors, the emergence of a color wheel or a spherical organization isn’t coincidence — it’s a meaningful representation that aligns with human understanding of color.

If we can demonstrate reliable control over a model’s internal representation with color, it suggests we might achieve similar control in more complex domains. We assume that the core mechanisms of embedding and representation remain similar even when the domains differ greatly in complexity.

Experimental approach

Our experiments used a simple architecture: a multilayer perceptron (MLP) autoencoder with a low-dimensional bottleneck. This architecture forces the model to compress information into a small number of dimensions, revealing how it naturally organizes concepts.

Architecture

We used a 2-layer MLP autoencoder with RGB colors (3 dimensions) as input and output, and a 4-dimensional bottleneck layer. While RGB data is inherently 3-dimensional, we needed a 4D bottleneck because of our unitarity (hypersphere) constraint, described below.

This architecture creates a useful tension: the model must balance information compression against the structural constraints imposed through regularization.

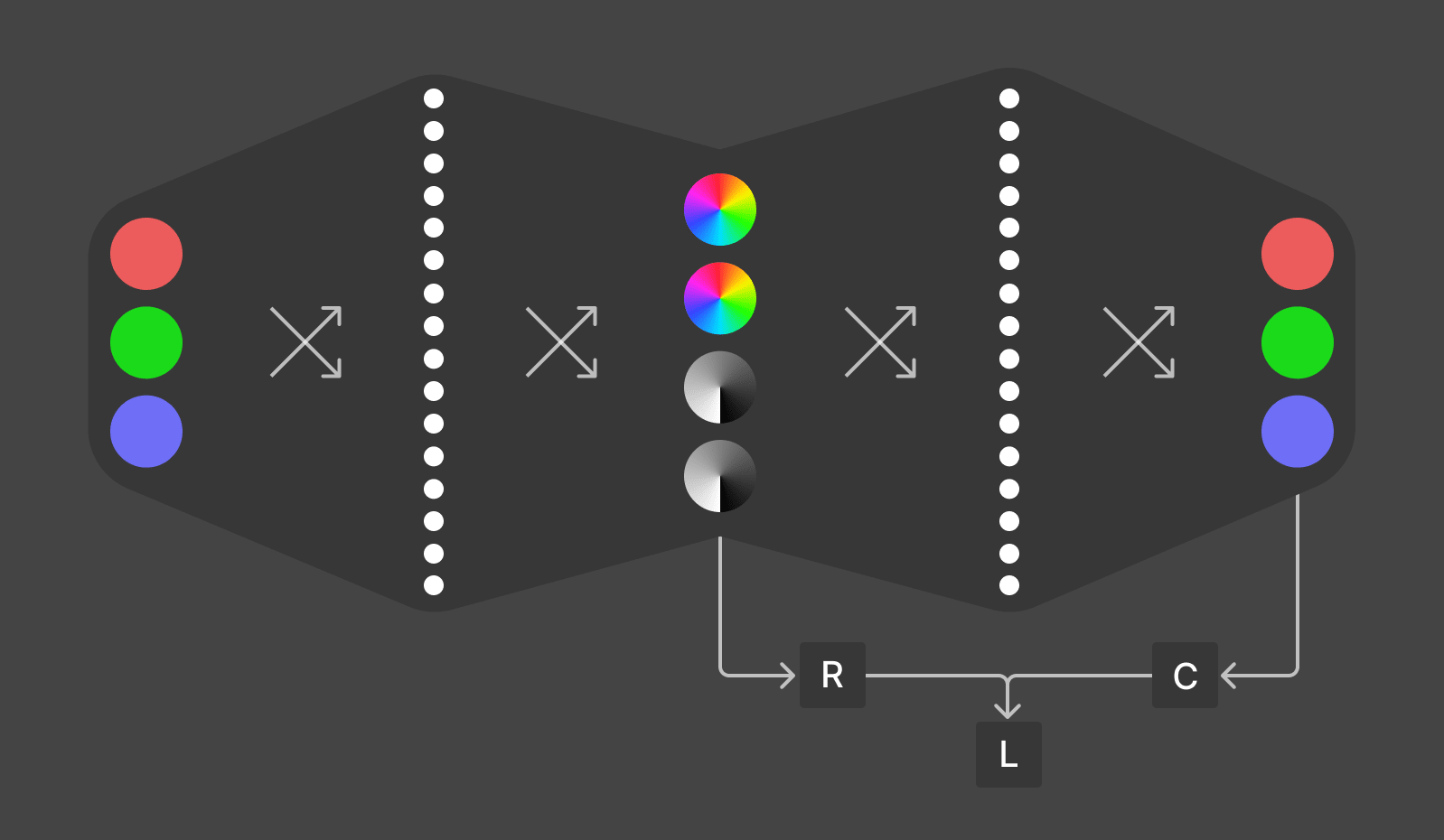
A neural network architecture diagram showing an MLP autoencoder with bottleneck structure. There are 5 layers. From left to right: the RGB input (three nodes colored red, green, and blue), then a stack of 16 white nodes, then four nodes for the latent space, two of which are filled with a rainbow gradient and two that are grayscale. The design is then reflected, with another 16 white nodes and the RGB output. Grey lines connect each layer to the next, forming the shape of an hourglass on its side. The structure illustrates how RGB color information is compressed into the 4D bottleneck representation and then reconstructed. Flowchart-like arrows connect from the middle and right layers to labelled boxes representing the loss terms. The middle (latent space) layer connects to the box labelled R for 'regularization'; the right (output) layer connects to a box labelled C for 'criterion'; both of those connect to a box labelled L for 'loss'. — **MLP Autoencoder Architecture** with RGB inputs/outputs (3 dimensions) and a bottleneck layer (4-dimensions). R: Regularization terms from the bottleneck layer. C: reconstruction loss criterion from the output layer. L: combined loss.

Regularization

We imposed structure through several complementary regularization techniques:

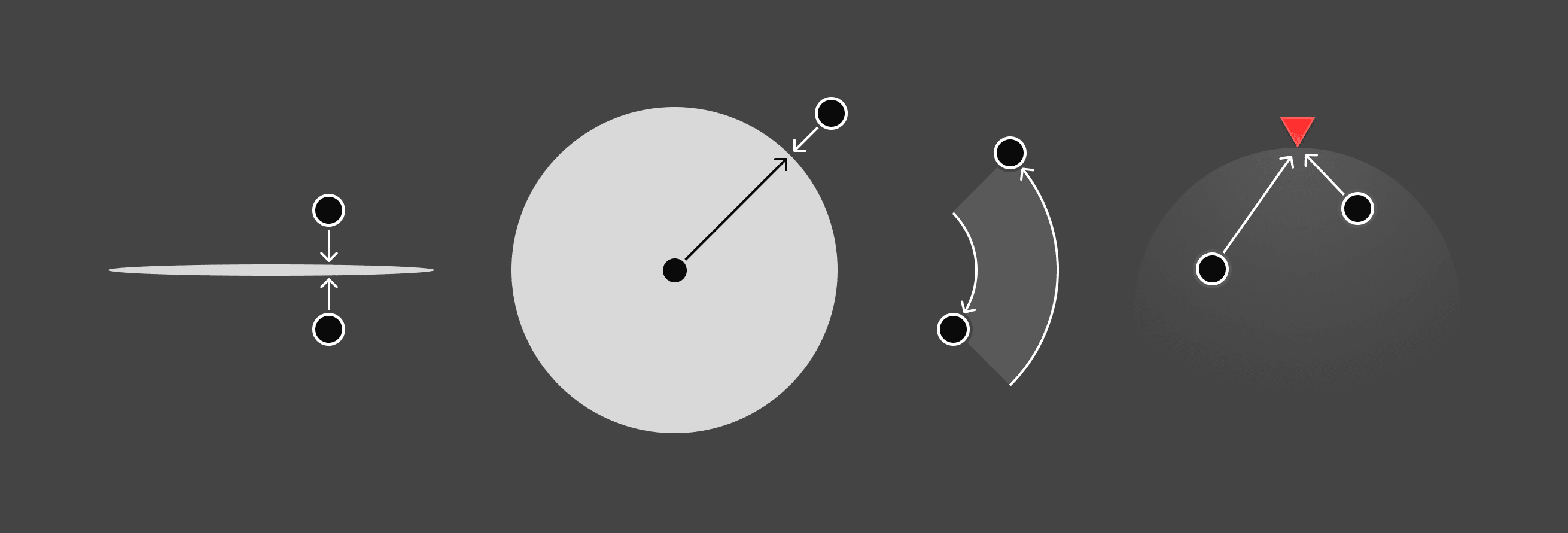
Planarity penalized embeddings for using dimensions beyond the first two (using L2 norm on the 3rd and 4th dimensions with target length 0), encouraging the model to organize hues in a plane.

Unitarity encouraged embedding vectors to have unit length (using L2 norm on all dimensions with target length 1), pushing representations toward the surface of a hypersphere^[14].

Angular repulsion encouraged distinct concepts to maintain distance from each other in the embedding space using cosine distance.

Concept anchoring explicitly pushed certain colors (like red) toward predetermined coordinates in the latent space using Euclidean distance. In retrospect, cosine distance might have been more appropriate given the spherical nature of our embedding space.

Conceptual diagram illustrating the four regularization terms used in our experiments, displayed against a dark gray background. From left to right: (1) Planarity: depicted as a horizontal disc with two white circles on opposite sides and arrows pointing vertically toward the plane, representing the constraint that keeps certain dimensions close to zero; (2) Unitarity: shown as a large circle with a black center point and a white point on the perimeter, with an arrow suggesting movement toward the circumference, representing the constraint that vectors maintain unit length; (3) Repulsion: illustrated as white circles placed on either end of an arc, each one with an arced arrow pointing to the other, representing how distinct embeddings are encouraged to maintain distance from each other; (4) Concept anchoring: visualized as two white circles being pulled toward a red triangle (representing the "red" concept), showing how certain colors are guided toward predetermined coordinates in latent space. — **Illustration of regularization terms.** From left to right: planarity, unitarity, angular repulsion, concept anchoring.

Labels

We applied these regularization terms selectively to different samples based on stochastic binary labels. The probability of a sample receiving a particular label was determined by formulas that capture the relevant color properties.

For the “red” label (measuring proximity to pure red), we calculated:

red = {(r - \frac{r g}{2} - \frac{r b}{2})}^{10}

This formula yields high values for pure red (r=1, g=0, b=0) and rapidly diminishing values as green or blue components increase. The exponent of 10 creates a sharp falloff.

For the “vibrant” label (measuring proximity to any pure hue):

vibrant = {(s \times v)}^{100}

Where s and v are saturation and value in the HSV color space. The high exponent (100) creates an extremely sharp distinction between fully saturated, bright colors and even slightly desaturated or darker ones.

These continuous probabilities were then scaled (multiplied by 0.5) and converted to binary labels by comparison with random values. For example, pure red would be labeled “red” approximately 50% of the time, while colors progressively further from red would be labeled with rapidly decreasing probability.

This stochastic approach effectively creates a form of weak supervision, where the model receives imperfect, noisy guidance about concept associations. We designed it this way to simulate real-world scenarios like labeling internet text for pretraining, where labels might be incomplete, inconsistent, or uncertain. Our experiments show that such sparse, noisy signals can still effectively shape the latent space—an encouraging finding for applications where comprehensive labeling is impractical.

Key findings

Our experiments produced several interesting results:

Predictable structure

The 4D latent space organized itself into a coherent structure where similar colors clustered predictably. When projected onto the first two dimensions, vibrant hues formed a clear circle resembling a color wheel, despite never explicitly telling the model to arrange them in this way.

Latent space visualizations showing three different 2D projections of the 4D embedding space at step 10000, alongside smaller thumbnails showing the evolution of the space during training. The left panel [1,0] (hue) shows a circular arrangement of colors forming a color wheel. The middle and right panels [1,2], [1,3] show similar circular structures from different angles. Thumbnails below show how the space evolved from a small cluster at step 0 through various transformations, eventually forming a spherical structure by step 8000. — **Top row:** Latent space visualizations showing three different 2D projections of the 4D embedding space at the end of training. **Left:** the hue plan (first two dimensions), with red at the top. **Middle and right:** one hue and one other dimension each. **Bottom row:** select frames showing the evolution of the space during training.

Importantly, we didn’t need to search for interesting projections after training. The structure formed as we intended due to regularization. While dimensionality reduction techniques often produce meaningful visualizations, what distinguishes our approach is the predictability and consistency in placing specific concepts in predetermined locations. This addresses a fundamental challenge in interpretability: knowing where in the latent space to look for specific concepts.

Here’s a similar visualization, this time as a video.

The video^[15] (and also the thumbnails in the figure above) shows the evolution of latent space:

Initially (step 0), all colors cluster at a single point
The space expands to form something resembling an RGB cube (around step 200)
The structure then contorts as the model balances reconstruction objectives against regularization constraints (steps 800-3000)
Around step 5000, coinciding with increased unitarity regularization, the structure becomes more spherical
Through the remainder of training, it settles into an increasingly regular sphere.

The video also shows how the hyperparameters were varied over time, and the regularization loss terms.

Effectiveness of minimal concept anchoring

Even with only a single anchored concept (red at coordinates $(1, 0, 0, 0)$ ), the entire latent space organized itself relative to this point. The other primary and secondary colors took positions spaced around the circle at regular intervals. This happened despite:

The anchoring regularization being applied inconsistently (pure red was only labeled as “red” 50% of the time)
The anchoring signal being applied stochastically based on noisy labels
No colors other than red being anchored to a point (although notably, vibrant colors were anchored to the plane formed by the first two dimensions).

We observed that anchoring a single concept, combined with planar constraints, influenced how the model organized its latent space. While we only explicitly constrained a portion of the space (2 of 4 dimensions), the entire representation adapted to these constraints in our simple domain. This suggests potential for targeted regularization, though the extent to which such influence would propagate in higher-dimensional spaces (like those found in large language models) remains an open question.

Selective vs. curriculum-based regularization

One of our practical findings concerns the training methodology. We initially explored curriculum learning approaches where we gradually introduced more complex data. However, we discovered that simply training on the full color space from the beginning with selective regularization produced superior results:

More stable training dynamics
Better preservation of the learned structure
More consistent results across different random initializations

This went against our initial intuition, but it simplifies implementation: designing curricula is tricky, whereas training on full data with selective regularization is more straightforward.

Implications for alignment research

These initial results suggest some promising directions for concept-anchored representation engineering in an alignment context. While other approaches have explored structuring latent spaces through regularization, our specific exploration of anchoring minimal concepts during training with selective per-sample regularization offers several potential insights^[16]:

Structure can be guided through selective regularization. Targeted regularization can successfully impose predictable organization on latent space.
Stochastic labeling is sufficient. The effect persists even with noisy, stochastic application of regularization, suggesting we don’t need perfect or complete concept labeling.
Related concepts naturally cluster. The resulting structure places related concepts near each other in latent space, potentially enabling more precise interventions.
Minimal anchoring may influence broader organization. A small number of anchored concepts can influence the organization of the broader representation space without distorting the relationship between concepts.

These points suggest that anchored concepts might indeed act as attractors that organize related concepts in meaningful ways, though verification in more complex domains is needed.

Limitations

Despite these promising signs, we acknowledge significant limitations:

Domain simplicity: Color has intrinsic geometric structure that may make it uniquely amenable to this approach. The RGB color space is already low-dimensional with clear, objective distance metrics. Language concepts likely occupy a much messier, higher-dimensional manifold with less obvious geometric relationships. The ease with which we found a color wheel structure may not transfer to domains where the “natural” organization is less clearly defined.

Architectural simplicity: Our experiments used tiny MLPs with a few hundred parameters. Modern language models have billions or trillions of parameters with complex, multi-layer architectures. While some work exists on regularizing transformer latent spaces (e.g., ConceptX, LSRMT), applying our specific approach of concept anchoring during training to shape transformer representations presents challenges we have yet to explore, particularly given how attention mechanisms create context-dependent representations.

Unknown trade-offs: There may be significant performance trade-offs between regularized structure and model capabilities. If regularization forces the model to organize concepts in ways that aren’t optimal for its tasks, we might see degraded performance.

Supervision requirements: This technique requires some concept labeling. In language models, identifying and labeling instances of abstract concepts like “deception” or “harmfulness” is more subjective and challenging.

Despite these limitations, we remain optimistic. The robustness to noisy labeling, effectiveness of selective regularization, and the observed influence of our targeted constraints suggest that this approach deserves further exploration in more complex domains.

Next steps

Our work so far has focused on exploring whether we can create structured latent spaces through selective regularization. Next, we’d like to see whether we can use this structure to actually control model behavior. Our next experiments will explore:

Selective concept suppression: Can we reliably suppress specific colors (e.g., red) at inference time, using pre-determined directions in latent space? Ideally, this would affect red and red-adjacent colors while leaving others (like blue) untouched. This could suggest new approaches for controlling model capabilities.
Concept deletion: Beyond temporary suppression, can we modify the network to permanently remove specific capabilities by identifying and ablating the relevant weights?
Transformer architectures: Ultimately, we want to apply these techniques to transformer models, which presents additional challenges due to their attention mechanisms and context-dependent representations.

Conclusion

Our experiments explore how selective regularization can guide the formation of structured representations during training, potentially reducing the need for post-hoc interpretation. Using these adapted techniques, we created partially structured latent spaces where concepts we cared about were predictably positioned, while allowing the model flexibility in organizing other aspects of its representations.

While many of the individual techniques we’ve used have precedents in the literature on prototype learning, supervised autoencoders, and contrastive learning, our specific contribution lies in exploring: (1) how proactively structuring a portion of the latent space during training through stochastic weak supervision can yield predictable organization where it matters, (2) that explicitly constraining just one concept and one plane can influence nearby representations without dictating the structure of the entire space, (3) that the approach shows robustness to noisy, stochastic labeling, and (4) that such structured latent spaces can be shaped by selective per-sample regularization rather than comprehensive supervision.

These findings suggest that concept-anchored representation engineering could potentially provide a valuable approach for designing more interpretable and controllable neural networks, building on existing work in latent space structuring. Whether this approach can scale to language models and more complex domains remains an open question, but these initial results provide encouragement to continue exploring this direction. If we can reliably engineer the structure of relevant portions of latent representations during training, we might gain better tools for alignment—particularly for more precise control over what models learn and how they use that knowledge.

We welcome suggestions, critiques, and ideas for improving our approach. If you’re working on similar research or would like to collaborate, please reach out. For those interested in replicating or building upon our experiments, we’ve made our code available in z0u/ex-color-transformer, with Experiment 1.7 containing the implementation of the selective regularization approach described in this post.

^
In this work, we distinguish between the semantic “concepts” we’re interested in (like “red” or “vibrant”) and their representation in the model’s latent space, where related terms from the literature would include “latent priors” or “prototypes” — the anchor points or structures that guide how these concepts are encoded.
^
Kim, B., Wattenberg, M., Gilmer, J., Cai, C., Wexler, J., Viegas, F., & Sayres, R. (2018). Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (TCAV). International Conference on Machine Learning. arXiv:1711.11279
^
Hadjeres, G., & Nielsen, F. (2020). Attribute-based regularization of latent spaces for variational auto-encoders. Neural Computing and Applications. arXiv:2004.05485
^
Anders, C. J., Dreyer, M., Pahde, F., Samek, W., & Lapuschkin, S. (2023). From Hope to Safety: Unlearning Biases of Deep Models via Gradient Penalization in Latent Space. arXiv:2308.09437
^
Gabdullin, N. (2024). Latent Space Configuration for Improved Generalization in Supervised Autoencoder Neural Networks. arXiv:2402.08441
^
Wen, Y., Zhang, K., Li, Z., & Qiao, Y. (2016). A Comprehensive Study on Center Loss for Deep Face Recognition. DOI: 10.1007/s11263-018-01142-4 [open access version on GitHub]
^
Oliveira, D. A. B., & La Rosa, L. E. C. (2021). Prototypical Variational Autoencoders. OpenReview hw5Kug2Go3-
While the specific implementation of Prototypical VAE by Oliveira et al. was retracted due to methodological concerns, we include this reference to acknowledge that the concept of prototype-based regularization in latent spaces has also been explored in other studies.
^
Khosla, P., Teterwak, P., Wang, C., Sarna, A., Tian, Y., Isola, P., Maschinot, A., Liu, C., & Krishnan, D. (2020). Supervised Contrastive Learning. arXiv:2004.11362
^
Chen, T., Kornblith, S., Norouzi, M., & Hinton, G. (2020). A Simple Framework for Contrastive Learning of Visual Representations. arXiv:2002.05709
^
Grill, J.B., Strub, F., Altché, F., Tallec, C., Richemond, P.H., Buchatskaya, E., Doersch, C., Pires, B.A., Guo, Z.D., Azar, M.G., & Piot, B. (2020). Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning. arXiv:2006.07733
^
Achille A., Rovere M., & Soatto S. (2017). Critical Learning Periods in Deep Neural Networks. arXiv:1711.08856
^
Betley, J., Tan, D., Warncke, N., Sztyber-Betley, A., Bao, X., Soto, M., Labenz, N., & Evans, O. (2025). Emergent Misalignment: Narrow finetuning can produce broadly misaligned LLMs. arXiv:2502.17424
^
Epistemic status: 75%, based on: - Word2Vec and similar embedding approaches showing meaningful geometric structure—Recent mech interp work suggesting similar representation mechanisms across domains—Emergent misalignment research indicating models tend to discover similar representational patterns.
^
In upcoming experiments with transformers, we intend to use hypersphere normalization as in nGPT. We think that normalization helps the optimizer to find meaningful representations, and we expect our DevInterp research to be most useful with architectures that lend themselves to well-structured latent spaces in other ways.
^
As an aside: I’m fascinated by these animated visualizations of latent space. Seeing how the space changes for every batch has given me insights into potential hyperparameter tweaks that would have been hard to find otherwise. Perhaps carefully selected metrics could have given similar insight if viewed as a static line chart, but I don’t know which metrics they would be, nor how you could know in advance which ones to choose.
^
My confidence in these claims ranges from 90..60% (from top to bottom).